Java滑动窗口算法题目练习(附详细图文及代码)_Java

长度最小的子数组

题目解析：这里给我们一个全是正整数的数组和一个目标值，让我们找一段连续的区间，这个区间的值之和是大于等于目标值的，从这个数组中找到一个最小的区间长度，如果不存在的话就返回0
算法原理：1.首先我们是可以使用暴力解法，双重for循环进行遍历出所有的情况，当满足区间的值大于等于目标值的话就进行结果更新，反之继续向后操作，我们可以发现这里是有许多的是多余的，就像如果此时的这个区间的值已经大于这个目标值了，如果继续向后操作的话，这个数组是正整数数组，肯定还是大于等于目标值，但是长度变长了，我们要找到是最短的，因此我们可以不需要让其重复操作，直接开始下一次循环就行
2."同向双指针"也叫滑动窗口算法，这里我们可以使用left和right两个指针向同一个方向移动，并且不回退，此时的思想就和上面暴力解法优化思想一样，一直进行将right下标对应的值放入sum变量中，当sum>=target时候就可以将minlen更新了，此时不必将right向后移动了，只需要将left下标的值减去，让left向后移动，这样重复操作进行查找，直到right遍历完整个数组就完成了

class solution {
    public int minsubarraylen(int target, int[] nums) {
        int sum = 0;
        int len = integer.max_value;//刚开始定义长度是int可以表示最大整数
        int n = nums.length;
        for(int left = 0,right = 0; right < n;right++){
            sum += nums[right];//入窗口
            //结果判断
            while(sum >= target){
                len = math.min(len , right - left + 1);//结果更新
                sum -= nums[left++]; //出窗口
            }
        }
        return len == integer.max_value ? 0 : len;
    }
}

时间复杂度：o(n),空间复杂度：o(1)

无重复字符的最长子串

题目解析：这里就是给了我们一个字符串s,让我们在里面找出最长连续不重复的子串长度，如果是空字符串就返回0
算法原理：1.暴力解法+哈希表(判断字符是否重复出现)，就是将其字符串中所有情况全部遍历一遍，将其存放在哈希表中，遍历的过程中判断是否已经存放在哈希表中，如果存在这时候就更新结果，并就跳出内循环，就这样一直重复操作
2.滑动窗口+哈希表，上面的暴力解法中会出现一些多余的操作，这里我们用left和right这两个同向双指针，不回退，right用来遍历整个字符串并将其放入哈希表中，并当right下标的字符存放后发现其如果没重复就更新结果 ，如果存在重复，那肯定是此下标有重复的，这时候就将left对应的字符从哈希表中删除，但我们可能要删除很多次，因为我们并不知道其那个是重复的，所以此时是个循环，直到没有重复为止继续更新结果，就这样一直right放入窗口，判断是否有重复字符，有的话就一直出left到没有重复字符为止，更新结果，就这样一直到right遍历完整个字符串

我们这里是使用int类型的数组来模拟哈希表，因为字符对应的是ascll码值

因此我们可以根据每次存放将其下标的值++，大于1说明有重复的就进行出窗口

class solution {
    public int lengthoflongestsubstring(string ss) {
        int[] hash = new int[128];//这里使用数组来表示其hash，如果其对应的位置>1说明有重复的
        int len = 0;
        char[] s = ss.tochararray();//将其字符串转换成字符数组，方便后面使用
        //使用同向双指针，滑动窗口
        for(int left = 0,right = 0;right < s.length;right++){
            //入窗口
            hash[s[right]]++;//字符对应的ascll码值作为下标++
            //判断，如果>1，说明有重复的了，就要出窗口
            while(hash[s[right]] > 1){
                //出窗口
                hash[s[left++]]--;
            }
            //更新结果
            len = math.max(len,right - left+1);
        }
        return len;
    }
}

最大连续1的个数|||

题目解析：题目就是找到最大连续1的个数，并且最多可以反转k个0
因此我们可以将其题目转换成找出一个最长子数组并且里面0的个数步超过k个
算法原理：1.暴力枚举+count(记录当前区间0的个数)
2.滑动窗口+count(记录当前区间0的个数)

class solution {
    public int longestones(int[] nums, int k) {
        int len = 0;
        int n = nums.length;
        int count = 0;//用于统计当前区间0的个数
        for(int left = 0,right = 0;right < n;right++){
            //记录当前0的个数
            if(nums[right] == 0){
                count++;
            }
            //出窗口
            while(count > k){
                if(nums[left++] == 0){
                    count--;
                }
            }
            //更新结果
            len = math.max(len , right - left + 1);
        }
        return len;
    }
}

时间复杂度：o(n)，空间复杂度：o(1)

将x减到0的最小操作数

题目解析：就是给了我们一个目标值x让我们每次从nums数组最左边或者最右边找一个数，将其减去，减去就要从数组中移除这个数，就这样一直重复操作，找出一个最小操作数，我们可以发现这个问题十分繁琐，因为我们每次也不直到是从左边还是右边
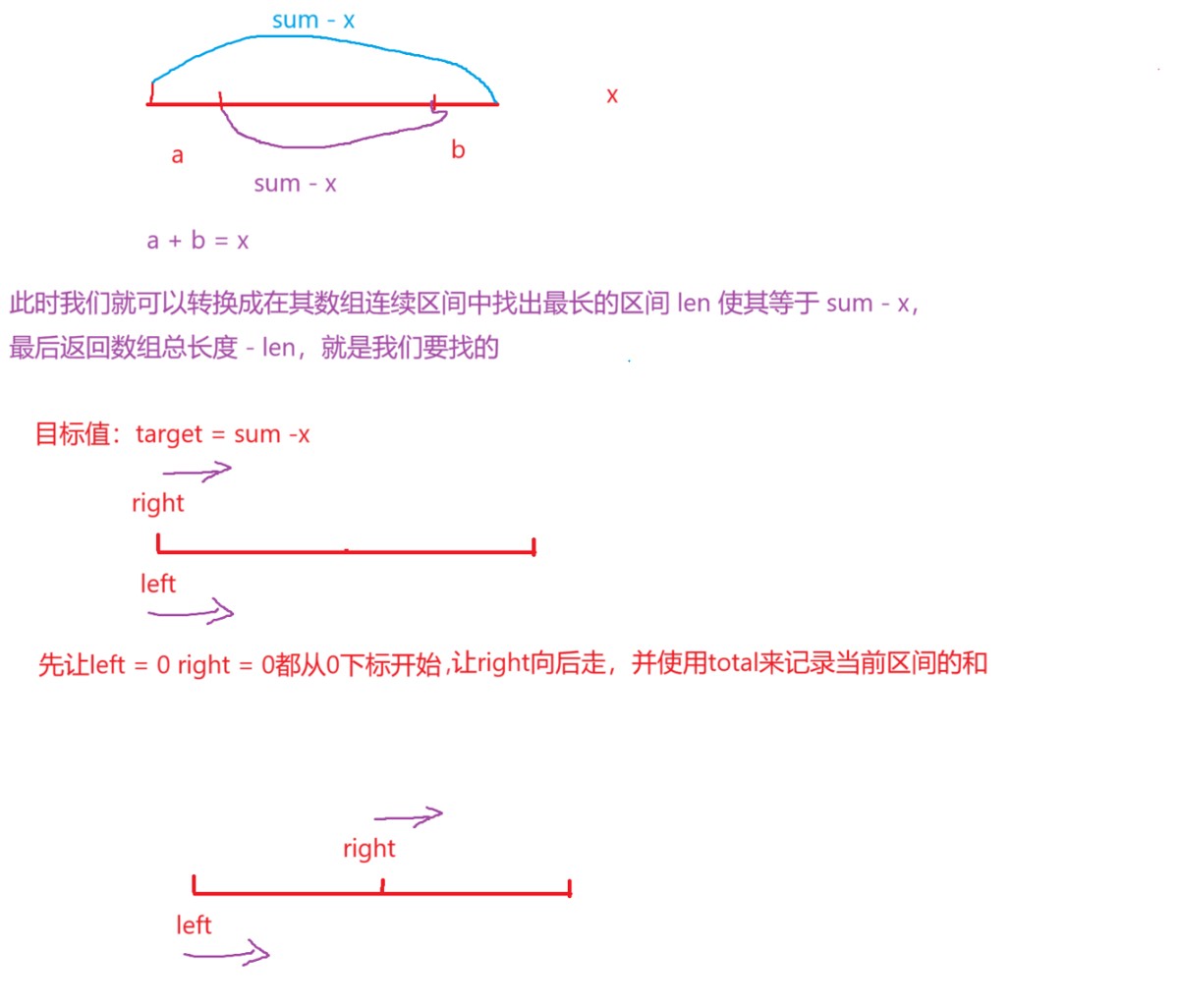
因此我们可以正难则反 我们可以将题目转换为在这个数组连续区间找一个最长的长度和为整个数组的和 - x，最后返回数组长度 - 找到的长度就行
算法原理：首先算出总的数组和sum ,我们的目标值target = sum - x，我们直接从数组中找出一个最长长度区间，使其值等于target
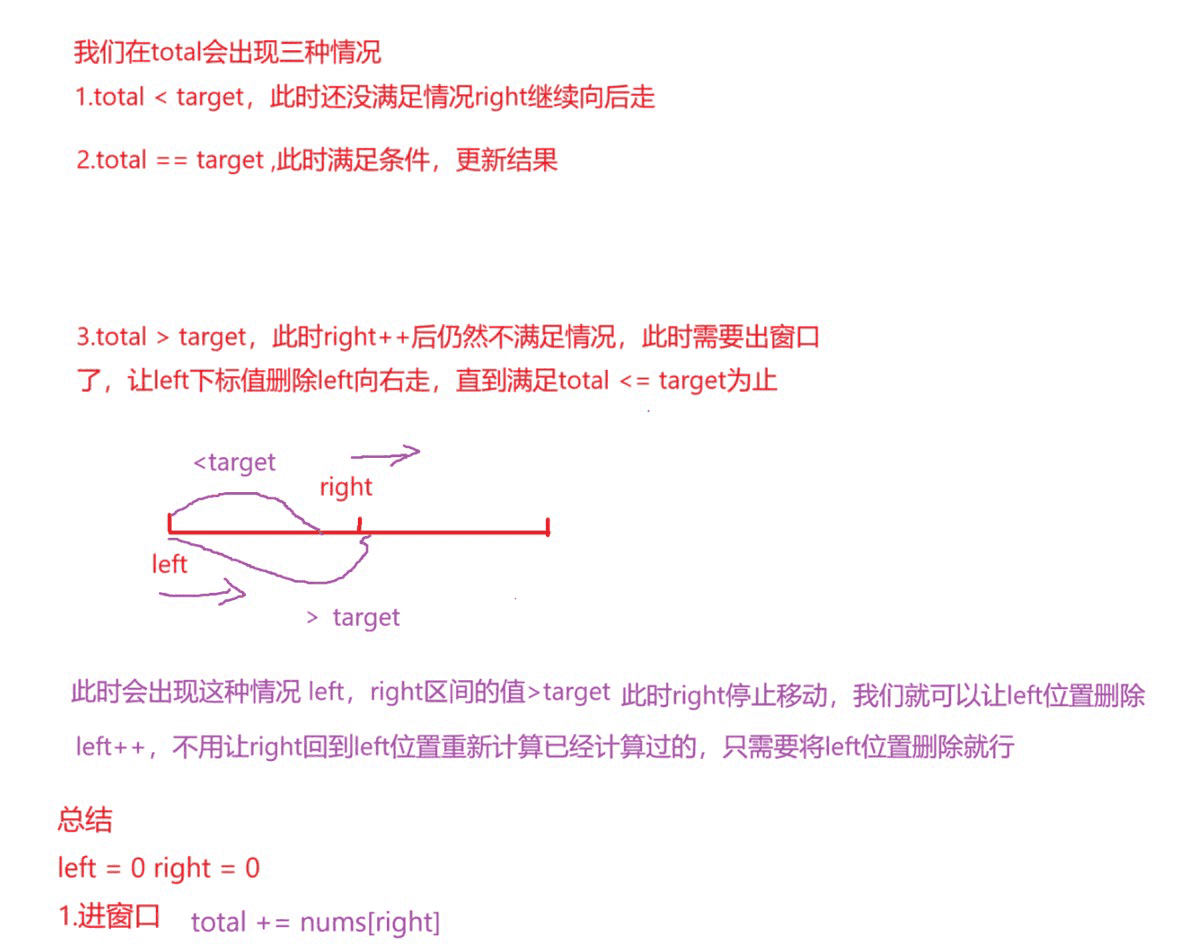
这里找到target目标值是采用滑动窗口即同向双指针，我们使用left和right两个指针，right遍历整个数组，total记录当前区间的值，
当 total == target时候就更新结果
当total > target就出窗口，删除left下标的值，并让left++，直到total <= target为止
反之就是小于，就一直将right下标的值入窗口

class solution {
    public int minoperations(int[] nums, int x) {
        //这里采用正难则反的思想，我们是每次从最右边和最左边找数相加，看何时等于x
        //我们可以转换为在这个数组连续区间找一个最长的长度和为 整个数组的和 - x
        int sum = 0;//nums整个数组的和
        int n = nums.length;
        for(int i = 0; i < n;i++){
            sum += nums[i];
        }
        //此时我们的目标值变成sum - x
        int target = sum - x;
        //如果全部sum和都<x说明找不到
        if(target < 0){
            return -1;
        }
        int total = 0;
        int len = -1;
        //后面就使用滑动窗口来找最长子串使其长度等于target目标值
        for(int left = 0,right = 0;right < n;right++){
            //入窗口
            total += nums[right];
            //判断
            while(total > target){
                total -= nums[left++];//出窗口
            }
            //等于的时候才更新结果
            if(total == target){
               len =  math.max(len,right - left + 1);
            }
        }
        return len == -1 ? -1 : n - len;
    }
}

水果成蓝

题目解析：就是给我们一个fruits数组，里面又好多种类，让我们用两个篮子放水果，并且每个篮子只能放一种水果，并且不可以跳着摘水果，遇到第三种水果直接停止采摘，获取其中最多摘多少水果
问题可以转换为：找出一个最长的子数组，并且里面不超过两种水果
算法原理：暴力解法+hash，可以使用双重for循环进行遍历，left和right这两个变量，但是其中有一些多余的操作，例如当水果的种类大于2时，我们此时采用的是，让left++,right回到left的位置继续进行遍历，但是我们可以发现，原本[left,right]这个区间种类>2，让其回去，此时让left++,其中的中类要么不变，要么减小，肯定不会增加
滑动窗口+hash
先不断的将right下标放入hash中
当种类>2的时候就要出窗口left下标对应的水果数量–，当其是0的时候说明其种类减少，将其从hash中删除，left++
更新结果
len = math.max(len,right - left+1)

class solution {
    public int totalfruit(int[] fruits) {
        //此时我们使用一个数组来实现hash
        int n = fruits.length;
        int[] hash = new int[n+1];
        int len = 0;//最长的长度
        for(int left = 0,right = 0,kinds = 0;right < n ;right++){
            //入窗口
            if(hash[fruits[right]] == 0){
                kinds++;//如果这个窗口没有添加过这个元素，此时种类增多
            }
            hash[fruits[right]]++;
            //当kinds>2进行出窗口
            while(kinds > 2){
                //出窗口
                hash[fruits[left]]--;
                //此时如果这个连续的区间没有了这个元素，此时的种类就减小
                if(hash[fruits[left]] ==0){
                    kinds--;
                }
                left++;
            }
            //更新结果
            len = math.max(len,right - left + 1);
        }
        return len;
    }
}

时间复杂度：o(n)
空间复杂度：o(n)

找到字符串中所有字母异位词

字母异位词是通过重新排列不同单词或短语的字母而形成的单词或短语，并使用所有原字母一次。

题目解析：就是给我们s和p两个字符串，让我们再s中找到所有p的异位词子串，并将其索引，最后返回其中所有的索引
算法原理：首先我们想到的是暴力解法+hash，一直遍历s串中所有和p长度相同的子串，并且要同过hash比较其中是否相同，相同就将其下标放入一个集合中，但是仍有一些多余的部分
滑动窗口+hash：left = 0,right = 0
使用left和right来确定窗口，并且此时的窗口长度是一定的，不断让right向后走，left也想后走，right并不需要回头，因为我们要进入下一个窗口仅需将left下标对应的字符出hash，将right+1下标入hash就行,此时就进入下一个窗口，让后进行判断是否相同就行

class solution {
    public list<integer> findanagrams(string ss, string pp) {
        list<integer> ret = new arraylist<>();

        char[] s = ss.tochararray();
        char[] p = pp.tochararray();
        //使用两个数组来模拟hash
        int[] hash1 = new int[26];//用来放pp字符串的所有字符信息
        for(char ch : p){
            hash1[ch - 'a']++;
        }
        int[] hash2 = new int[26];//此时的用来放窗口中每个字符出现的次数
        int n = pp.length();
        //此时的count是用来统计有效字符个数
        for(int left = 0,right = 0,count = 0;right<ss.length();right++){
            char in = s[right];
            if(++hash2[in - 'a'] <= hash1[in - 'a']){//入窗口
                count++;
            }
            //判断
            if(right - left + 1 > n){
                //出窗口
                char out = s[left++];
                if(hash2[out - 'a']-- <= hash1[out - 'a']){
                    count--;
                }
            }
            //更新结果
            if(count == n){
                ret.add(left);
            }
        }
        return ret;
    }
}

时间复杂度：o(n+m) ,两个字符串串长度
空间复杂度：o(n) ， s字符串长度

串联所有单词的子串

题目解析：就是在一个s字符串中找出包含words中所有单词，并返回所有下标，
算法原理：此题目和上一题：找出所有字母的异位词是一样的意思，只不过我们此时这里的字母变成了单词，因此这个题目和上一个原理一样，只不过此时要注意将其单词看成一个整体，这样就和上一个题目一样了

class solution {
    public list<integer> findsubstring(string s, string[] words) {
        list<integer> ret = new arraylist<>();

        //使用map来存放words
        map<string,integer> hash1 = new hashmap<>();
        for(string word : words){
            hash1.put(word,hash1.getordefault(word,0)+1);
        }
        int n = words[0].length();//单词长度

        int m = words.length;//有多少单词
        //此时要循环n次滑动窗口，因为我们将每个单词这些字符看成了一个整体放入hash
        for(int i = 0;i < n;i++){
            //使用count来统计有效单词个数
            map<string,integer> hash2 = new hashmap<>();
            for(int left = i,right = i,count = 0;right <= s.length() - n;right += n){
                string in = s.substring(right,right+n);
                hash2.put(in,hash2.getordefault(in,0)+1);
                if(hash2.get(in) <= hash1.getordefault(in,0)){
                    count++;
                }

                //出窗口
                if(right - left + 1 > m*n){
                    string out = s.substring(left,left+n);
                    if(hash2.get(out) <= hash1.getordefault(out,0)){
                        count--;
                    }
                    hash2.put(out,hash2.get(out) - 1);
                    if(hash2.get(out) == 0){
                        hash2.remove(out);
                    }
                    left += n;
                }
                if(count == m){
                    ret.add(left);
                }
            }
        }
        return ret;
    }
}

时间复杂度：o( m * n)
空间复杂度：o( n )
n是words数组长度，m是s的长度

最小覆盖子串

题目解析：在s这个字符串中找到一个最下子串，并且其中每个字母数量要不小于t中的
算法原理：
暴力解法：双重for循环+hash，双重for循环遍历所有情况，用hash存放，并有方法来判断其是否符合条件
滑动窗口+hash：left = 0 , right = 0;暴力解法中，我们遇到满足情况进行更新结果时候，其实并不需要将其right从新返回left，重新放入hash中，我们只需要将left下标对应字符出去就行，因为此时只会出现两种情况1.还满足条件right不动2.不满足条件 right继续右移

class solution {
    public string minwindow(string ss, string tt) {
        char[] s = ss.tochararray();
        char[] t = tt.tochararray();

        //使用数组来模拟hash
        int[] hash1 = new int[128];
        int kinds = 0;//记录tt中出现字符的种类
        for (char ch : t) {
            if (hash1[ch]++ == 0) {
                kinds++;
            }
        }

        int minlen = integer.max_value;
        int begin = -1;//记录其起始位置和长度即可
        int[] hash2 = new int[128];//记录窗口中字符
        for (int left = 0, right = 0, count = 0; right < ss.length(); right++) {
            char in = s[right];
            //当这个字符的数量和hash1相同时候，count++
            if (++hash2[in] == hash1[in]) {
                count++;
            }
            while (kinds == count) {
                //更新结果
                if (right - left + 1 < minlen) {
                    begin = left;
                    minlen = right - left + 1;
                }
                char out = s[left++];
                if (hash2[out]-- == hash1[out]) {
                    count--;
                }
            }
        }
        return begin == -1 ? new string() : ss.substring(begin, begin + minlen);
    }
}