计算相似度是许多机器学习和数据分析任务中的重要步骤,尤其是在推荐系统、文本分析和图像处理等领域。相似度的计算有多种方法,每种方法适用于不同类型的数据。本文将探讨如何在 python 中计算相似度,提供示例代码,并使用流程图和旅行图来表述我们的思路。
1. 相似度计算的基本概念
相似度是用来量化对象之间的相似程度的指标。相似度通常取值在 0 到 1 之间,值越接近 1 表示越相似。常见的相似度计算方法包括:
- 余弦相似度(cosine similarity)
- 欧氏距离(euclidean distance)
- 曼哈顿距离(manhattan distance)
- 杰卡德相似度(jaccard similarity)
2. 余弦相似度
余弦相似度是一种衡量两个非零向量夹角的相似度,计算公式为:
[ \text{cosine_similarity} = \frac{a \cdot b}{|a| |b|} ]
import numpy as np
def cosine_similarity(a, b):
return np.dot(a, b) / (np.linalg.norm(a) * np.linalg.norm(b))
# 示例
vector_a = np.array([1, 2, 3])
vector_b = np.array([4, 5, 6])
similarity = cosine_similarity(vector_a, vector_b)
print(f'余弦相似度: {similarity}')
3. 欧氏距离
欧氏距离是计算两点之间的“直线”距离,计算公式为:
[ \text{euclidean distance} = \sqrt{\sum (a_i - b_i)^2} ]
示例代码
from scipy.spatial import distance
def euclidean_distance(a, b):
return distance.euclidean(a, b)
# 示例
vector_a = np.array([1, 2, 3])
vector_b = np.array([4, 5, 6])
dist = euclidean_distance(vector_a, vector_b)
print(f'欧氏距离: {dist}')
4. 曼哈顿距离
曼哈顿距离计算两点在坐标轴上各分量的绝对差值的总和,计算公式为:
[ \text{manhattan distance} = \sum |a_i - b_i| ]
示例代码
def manhattan_distance(a, b):
return np.sum(np.abs(a - b))# 示例
vector_a = np.array([1, 2, 3])
vector_b = np.array([4, 5, 6])
dist = manhattan_distance(vector_a, vector_b)
print(f'曼哈顿距离: {dist}')
5. 杰卡德相似度
杰卡德相似度用于测量有限样本集合之间的相似性,计算公式为:
[ \text{jaccard similarity} = \frac{|a \cap b|}{|a \cup b|} ]
示例代码
def jaccard_similarity(set_a, set_b):
intersection = len(set_a.intersection(set_b))
union = len(set_a.union(set_b))
return intersection / union
# 示例
set_a = {1, 2, 3}
set_b = {3, 4, 5}
similarity = jaccard_similarity(set_a, set_b)
print(f'杰卡德相似度: {similarity}')
6. 流程分析
计算相似度的基本流程如下:
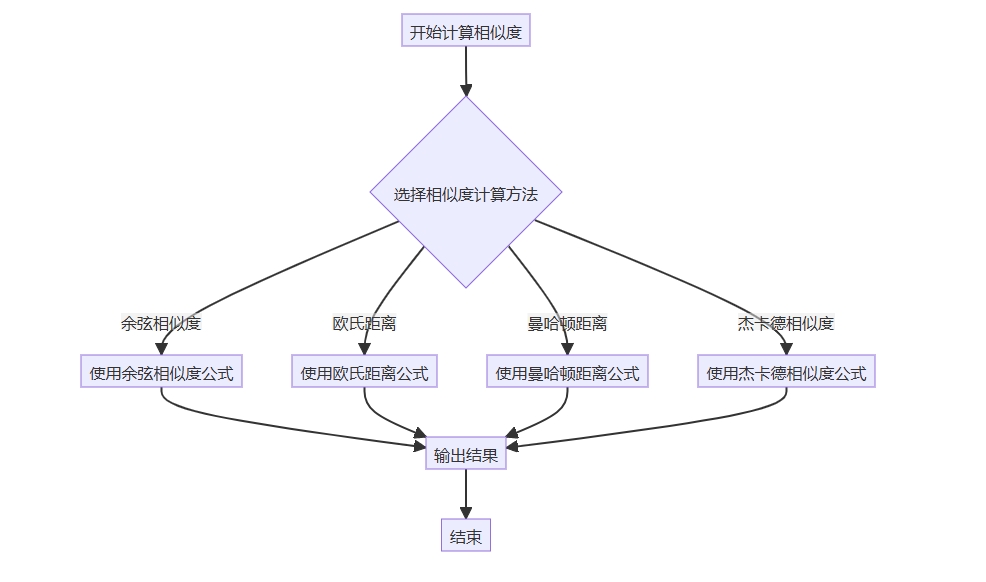
7. 旅行图
在数据分析的旅程中,我们可以将每个步骤视为旅途中的一个环节,以下是我们的数据计算之旅:
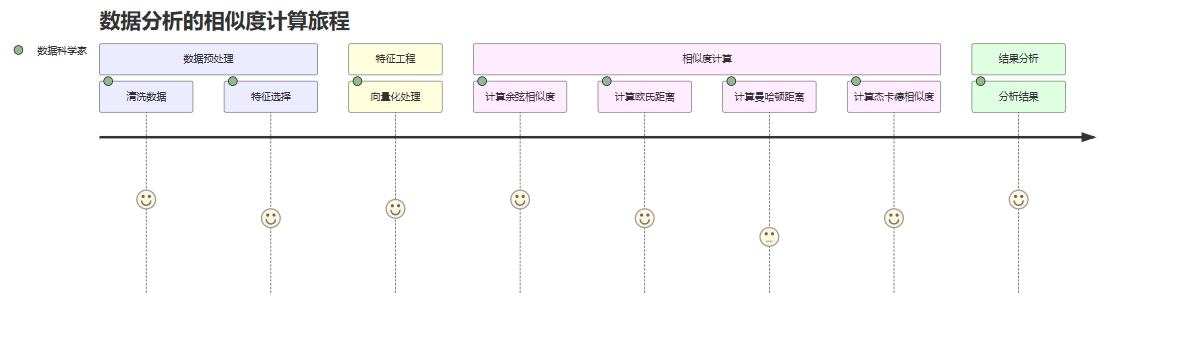
到此这篇关于python中计算相似度的方法详解的文章就介绍到这了,更多相关python计算相似度内容请搜索代码网以前的文章或继续浏览下面的相关文章希望大家以后多多支持代码网!




发表评论