一、问题介绍
1.1:编码问题
首先,我们知道,数字字符等任何数据的底层,都是以二进制(0,1序列)的方式存储在计算机内的。
对于“编码”其实就是那些能显示在计算机屏幕上的:不同字母、汉字、字符所分别对应的二进制序列的一种映射关系。
通常的编码方式有固定长度编码和不定长度编码两种。
固定长度编码:就是每一个字符对应的二进制01序列的长度是相同的,不如unicode、utf-8、gb2312、gbk,acsii都是定长编码
优点:每个字符对应的字符序列长度相同,易读取(不会产生二义性问题,依次往后按照固定长度读取即可得到字符)
缺点:计算机的传输资源(带宽)是有限的,如果每个字符都是等长的,当有的字符频率高,有的字符频率低,有的字符可能根本没出现,其实再使用等长编码就会浪费资源。
举例:
| 字母 | 二进制 |
|---|---|
| a | 000 |
| b | 001 |
| c | 010 |
| d | 011 |
| e | 100 |
| f | 101 |
| g | 110 |
| h | 111 |
在这种编码下,如果文件内容是“abcdefgh"或者几个字符出现次数都比较均匀的情况下,这种编码方式其实也行,但是很多情况,有的字符频率会特别高,有的字符会特别低,如果整个都采用相同长度的编码,会浪费存储和传输资源。如果 让那些频率高的字符对应存储的二进制序列长度短,而频率低的可以适当长一些, 这样就可以大量减少资源的浪费了。
于是产生了不定长编码
不定长度编码:它的设计思想就是始得总体的编码长度之和尽可能小。不定长编码需要解决以下两个关键问题
-
“编码不可以有二义性”: 即一个字符的编码不可以是另外一个字符的前缀码,否则无法判断这是一个字符还是一个字符的一部分,比如:“01”和“010”就不能同时作为两个不同字符的编码。
-
”编码长度尽可能短": 让出现频率高的字符的编码长度短,而频率低的字符编码可以稍长;从而压缩总共的存储空间,提高传输的速度。
优点:很明显,存储空间压缩,传输性能提升。
缺点:设计时需考虑避免二义性问题。
不定长编码有多种,而如何设计,能让一段文字对应的编码长度总和最短呢?—— 哈夫曼编码:一种【贪心思想】的不定长编码策略,能使总编码长度最短。
二、哈夫曼编码
2.1:目标:最小化带权路径长度和wpl
不定长编码首要解决的问题是: “编码不可以有二义性"(即应该都为前缀码)。我们现在先把这个前提记在脑子里。
而编码过程通常就是不断在0,1之间在做选择的过程,所以在解决编码问题时,通常都会使用二叉树这种数据结构。
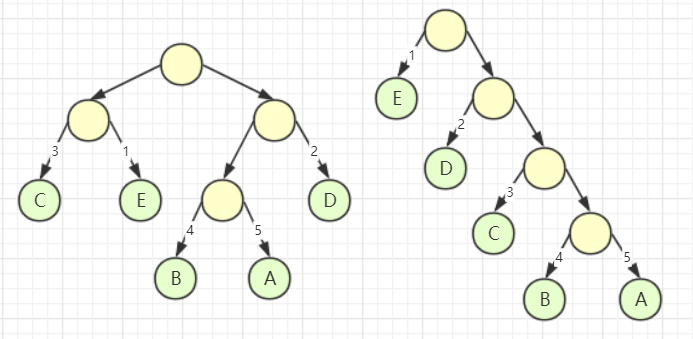
如上图所示,是使用二叉树进行给字符编码的示例,自顶而下每条边代表0或1,遍历到那个节点,这条边上的0,1序列即为其字符的编码。但是考虑到上文说到的前缀码问题,我们编码的字符必须只能是这颗树上的叶子节点(你可以看到,如果非叶子节点,那么必然这个字符的码是其他字符码的前缀!!!)。
当我们为需要编码的字符构建这样一颗使叶子节点是需要编码的字符的二叉树,我们就得到了各个字符的边长编码。
- 编码为从根节点出发,到该字符叶子节点路径上的边的
0,1序列 - 长度为根节点到该字符叶子节点的长度。
等等,那么我们该如何构建呢?或者说,如何构建一颗最优的非定长编码二叉树?
我不想直接说哈夫曼编码,我想一步一步,能不能我们自己推出来哈夫曼编码这个算法!站在前人肩膀上固然是好的,但是有的时候思维总是受限,殊不知前人得出这个绝妙想法也是有一个思想的轨迹的,或许是受到知识的诅咒,总是拆掉获取真理的那个阶梯而直接向世人抛出结果,但我认为,真正珍贵的是,是他思考的轨迹!!!~~扯远了,这里从我自己思考哈夫曼编码的思考轨迹出发,来试着摸索着哈夫曼编码是如何被提出的…
ok,我们构建定长编码的本意就是为了压缩存储空间,我们的目的就是: 在当前字符和其频率确定的情况下,为其设计一种编码方式,最小化其存储空间!
既然我们有了对字符编码的这棵二叉树,那么我们在这个二叉树上,可以以二叉树相关问题的形式把我们的这个目标描述一下,这也是我们之后基于这么一颗编码二叉树求解的核心。
在这之前,我们需要对以下概念有一些了解:
| 概念 | 定义 |
|---|---|
| 路径 | 从树中一个结点到另一个结点之间的分支构成这两个结点之间的路径 |
| 路径长度 | 路径上的分支数目 |
| 树的路径长度 | 从树根到每一结点的路径长度之和 |
| 权 | 赋予某个实体的一个量,是对实体的某个或某些属性的数值化描述。在数据结构中,实体有结点(元素)和边(关系)两大类,所以对应有结点权和边权。结点权或边权具体代表什么意义,需要具体问题具体分析。如果在一棵树中的结点上带有权值,则对应的就有带权树等概念。 |
| 结点带权路径长度 | 从该结点到树根之间的路径长度与结点上权的乘积 |
| 树的带权路径长度(wpl) | 树中所有叶子结点的带权路径长度之和,通常记作 wpl |
还是以下面两棵编码树举例,其实如果以1bit为单位,我们所需要的存储空间就是 树的带权路径长度(wpl)

左树 wpl:1 × 2 + 3 × 2 + 2 × 2 + 4 × 3 + 5 × 3 = 39
右树 wpl:1 × 1 + 2 × 2 + 3 × 3 + 4 × 4 + 5 × 4 = 50
所以我们利用编码二叉树求解最优非定长编码的目标就是:最小化带权路径长度(weighted path length,wpl),即所有字符的频率乘以其在树中的路径长度的总和。
2.2:如何最小化wplor如何构建最优编码二叉树:贪心
还是上面两棵二叉树的图,那么如何构建这样一颗二叉树呢?我们现在知道是叶子节点(也就是待编码的字符), 如何利用这些带权叶子节点构建一颗wpl最小的编码二叉树?我们想要wpl尽量小,我们就要让频率小的叶子节点尽量都往树的底下靠(这样路径长,但由于频率小,对总wpl的影响小),频率较高的叶子节点尽量靠近根节点, 这样还不够,还需要使总共的wpl也最小。
1、方法1:自顶向下❌
构建树,我们往往会很自然而然的想到自顶向下,本着让频率小的叶子节点尽量都往树的底下靠(这样路径长,但由于频率小,对总wpl的影响小),频率较高的叶子节点尽量靠近根节点的目的,我们 自顶向下,每次选择频率最高的叶子节点作为根节点的孩子,如果还有频率次高,则再作为子孩子,这样可以吗?
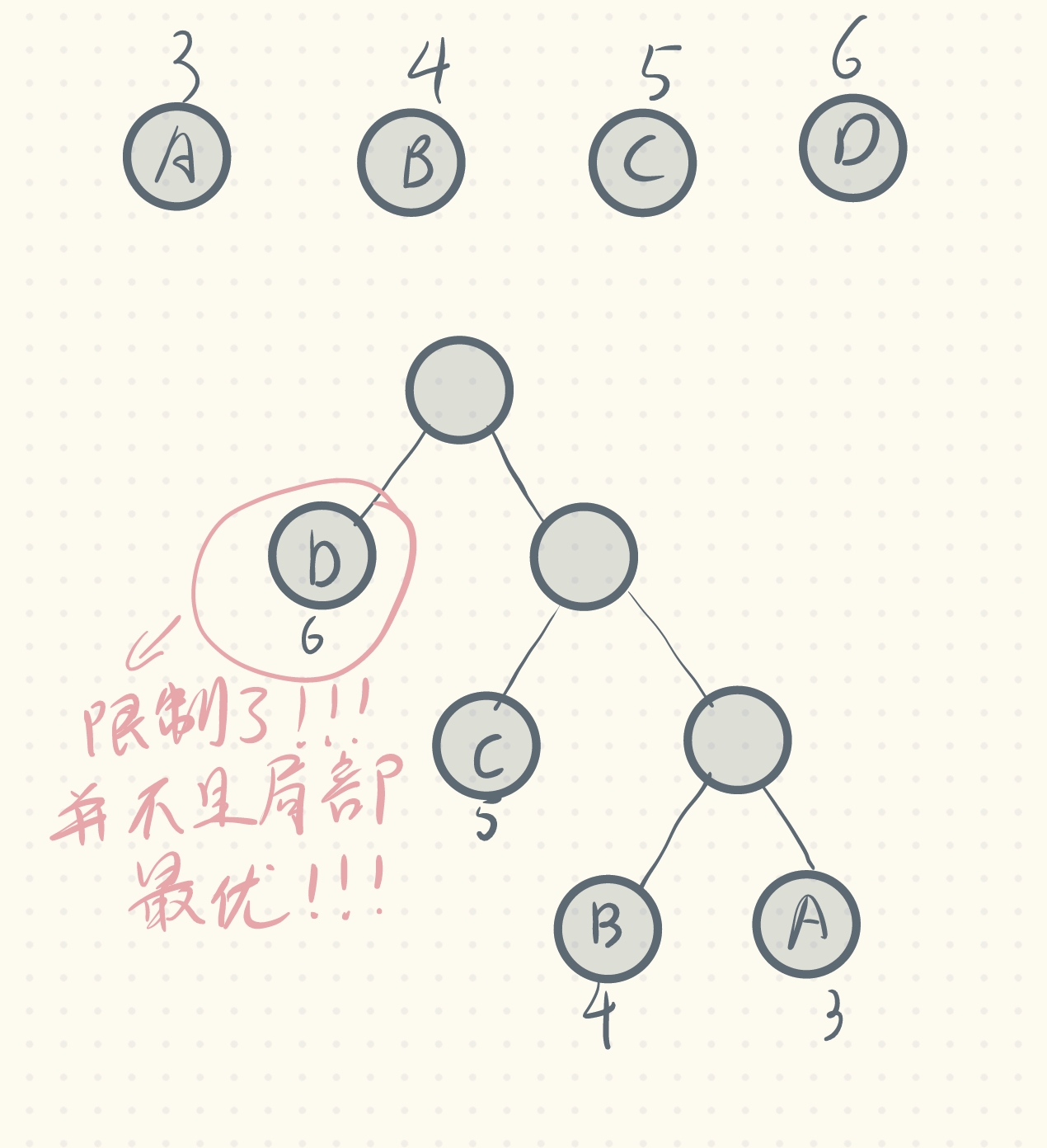
但是你发现,虽然我们把频率由高到低,依次从根节点往下放,听起来很合理,但其实得到的结果并不是全局最优!!!因为我们做选择就不是局部最优,比如我们把d放在根节点的左孩子位置,其实这不是一个局部最优的做法,因为这就意味着这个分支不能往下存在叶子节点。比如我很容易就能找出下面这个反例,它的wpl就比上面那棵树的低:
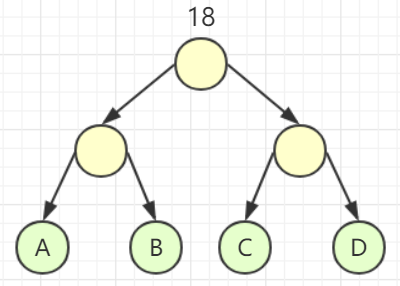
既然自顶向下构建不行,那么自底向上呢??
🪧毕竟我们都知道这棵树的叶子节点了,只要我们把这些叶子节点进行合并,依次由底向上,也可以构建一颗编码树,但是注意,我们还是要思考如何能获得一个最优(wpl最小)的编码二叉树!!
2. 方法2:自底向上✅
首先先不管wpl怎么最小,我们看看如何由叶子节点自底向上构建二叉树吧。
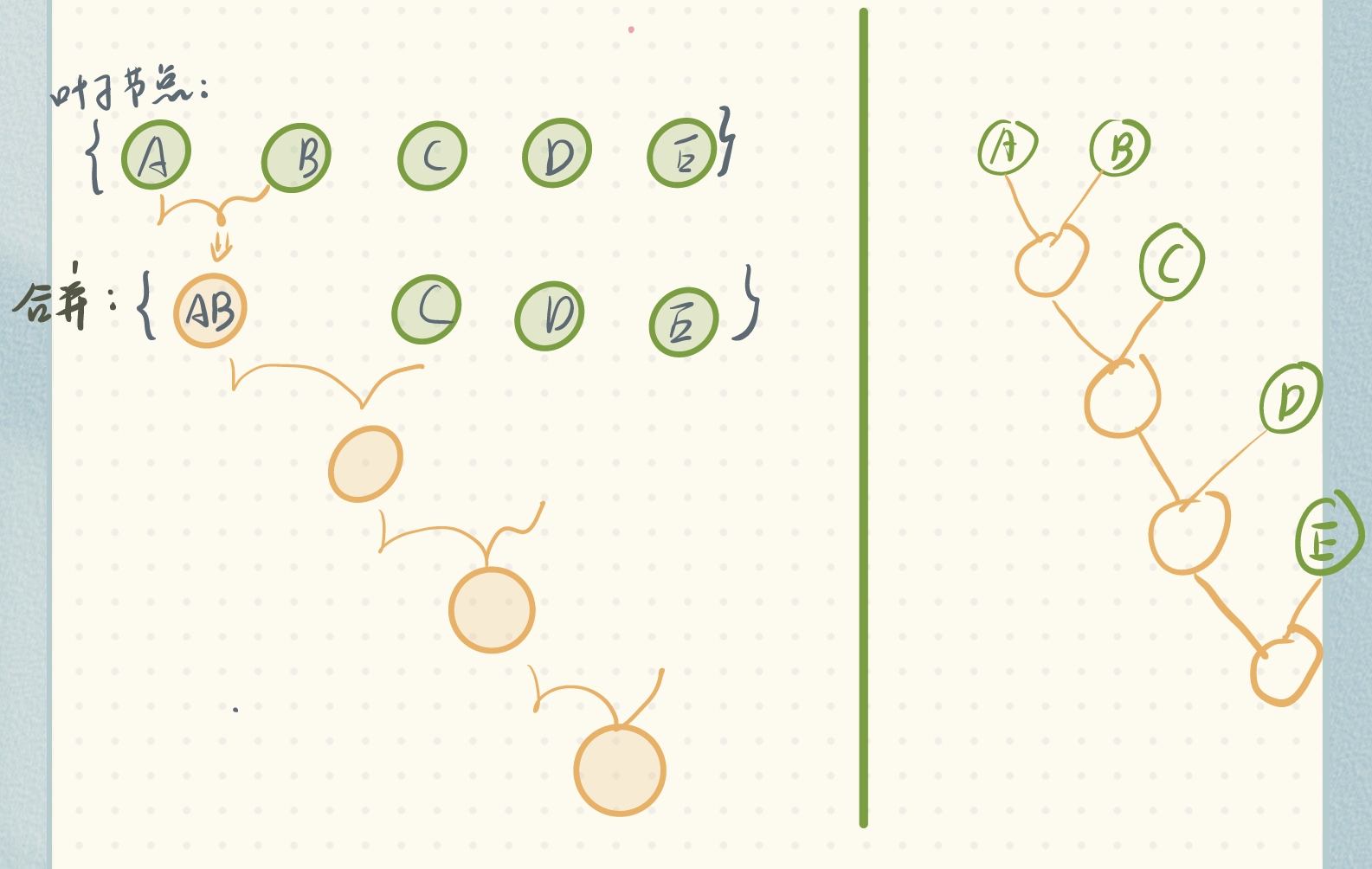
上图只是自底向上由叶子节点构建二叉树的其中一种方式,我们需要get到的核心是构建的步骤:
- 取两个叶子节点合并成一个新节点
- 将新节点加入到叶子节点集合
- 重复1,2直到叶子节点集合为只剩一个节点
ok,明白了如何由叶子节点构建二叉树,我们现在需要思考的就是我们的目标本身了:如何使这个二叉树的wpl(带权路径和)最小?
同样的,本着让频率小的叶子节点尽量都往树的底下靠(这样路径长,但由于频率小,对总wpl的影响小),频率较高的叶子节点尽量靠近根节点的目的:
- 首先选频率最小的两个节点合并,得到新节点(其权值为两个频率最小节点的权值和)——局部最优
- 将得到的新节点加入叶子节点集合
- 重复1,2
- 直到叶子节点集合只剩一个节点——全局最优

上面这个步骤明显是一个贪心过程:我们贪的就是在由叶子节点构建二叉树时,总是选择节点集合中频率最小的两个进行合并!
为什么这个贪心的局部最优成立?关键在于:将叶子节点进行合并成新节点后,得到的新节点频率是从这个集合中任意选出两个节点合并最低的,这让他在后续构建过程中可以被优先合并(处于这棵树的较低层);同时,不像自上而下,构建出的新节点并不会限制后续的构建过程(不会影响全局最优)。
说实话贪心确实挺难证明的,一般情况下,你只要举不出反例,其实就是ok的。就比如说最典型的一个贪心,有一堆钱,你只能拿十张,你是不是每次都是拿里面最大的,拿完十张就是整体最大;那我要你证明,其实你说该怎么证明呢?也不好证明。
像下面这张图展示的,如果每次不是从节点集合中选择频率最小的,其实最后得出来的结果就是没有上面那种大
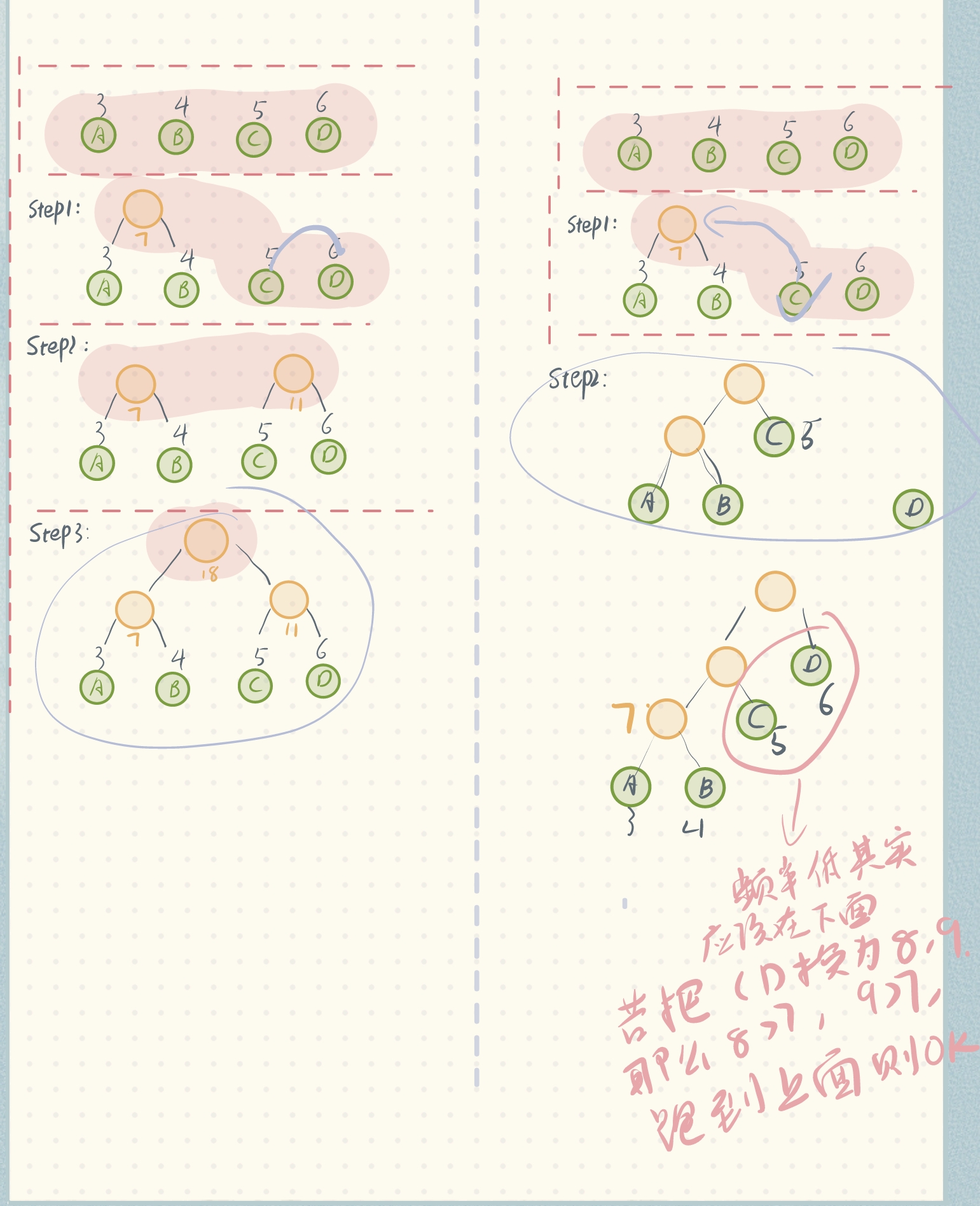
2.3:自顶向下的贪心思想
虽然上面讨论出来,在构建二叉编码树这个过程,的确是自底向上的,但是它所用到的贪心思想确实是:自顶向下。为什么这么说呢?
原问题有n个节点,通过贪心选择合并两个频率最低节点为一个新节点,将新节点加入到节点集合,进行n-1个节点的最优编码二叉树构建,可以看到,首先我们要承认使用贪心的前提是:问题具有贪心选择性质,即可以通过局部最优进而得到全部最优(并不是所有问题都具有贪心选择性质);而由局部最优得到全局最优其实是一个自顶向下的思想过程:通过每次当前的贪心选择,来缩小问题规模,从而一步一步得到全局最优解。
而动态规划则和分治是典型的自底向上的过程,通过小规模问题,向上推导or合并得到最终问题;而贪心则是一开始就站在了一个全局的视角(它必须这样看,否则不能判断当前局部最优是否能推导整体最优),通过贪心选择,来缩小问题规模。
所以我想说的是,自顶向下的是贪心的思想框架,而哈夫曼树构建的实际过程,的确是自底向上。
2.4:实现代码:
#include <iostream>
#include <unordered_map>
#include <queue>
using namespace std;
//1.定义哈夫曼树的节点
struct node{
char ch; //字符
int freq; //频率
node* left;
node* right;
//c++语法:构造函数
node(char character, int frequency): ch(character), freq(frequency), left(nullptr), right(nullptr){}
};
//2.比较函数,用于优先队列构建小根堆
struct compare{
bool operator()(node* node1, node* node2){
return node1->freq > node2->freq;
}
};
//3.哈夫曼树自底向上构建(传入字符+频率集合
node* buildhuffmantree(const unordered_map<char, int>& frequencies){
//小根堆(优先队列实现),用来存储实际节点node,且按频率大小排序
priority_queue<node*, vector<node*>, compare> minheap;
//创建叶子节点并且加入优先队列
for(const auto& pair : frequencies){
minheap.push(new node(pair.first, pair.second));
}
//自底向上合并节点并插入优先队列
while(minheap.size()>1){
//step1:取出频率最小的两个节点
node* leftnode = minheap.top();
minheap.pop();
node* rightnode = minheap.top();
minheap.pop();
//step2:合并
node* mergednode = new node('\0', leftnode->freq + rightnode->freq);
mergednode->left = leftnode;
mergednode->right = rightnode;
//step3:将新节点加入优先队列
minheap.push(mergednode);
}
//返回根节点
return minheap.top();
}
//根据哈夫曼树获取各个字符的哈夫曼编码——二叉树的遍历,prefix记录当前路径上的哈夫曼编码
void getcodes(node* root, const string& prefix, unordered_map<char, string>& huffmancodes){
if(!root) return;
//遍历边,寻找叶子节点
if(!root->left && !root->right){
huffmancodes[root->ch] = prefix;
}
getcodes(root->left, prefix+"0", huffmancodes);
getcodes(root->right, prefix+"1", huffmancodes);
}
//释放哈夫曼树内存
// 释放哈夫曼树内存
void freehuffmantree(node* root) {
if (!root) return;
freehuffmantree(root->left);
freehuffmantree(root->right);
delete root;
}
int main(){
// 输入字符和频率
unordered_map<char, int> frequencies;
int n;
cout << "enter the number of characters: ";
cin >> n;
for (int i = 0; i < n; ++i) {
char ch;
int freq;
cout << "enter character and frequency: ";
cin >> ch >> freq;
frequencies[ch] = freq;
}
// 构建哈夫曼树
node* root = buildhuffmantree(frequencies);
// 生成哈夫曼编码
unordered_map<char, string> huffmancodes;
getcodes(root, "", huffmancodes);
// 输出每个字符的哈夫曼编码
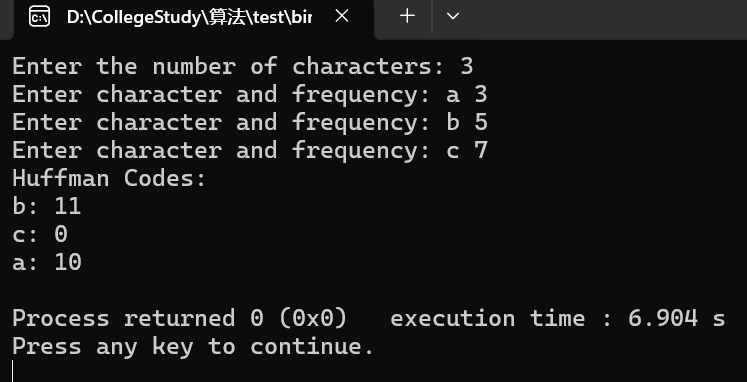
cout << "huffman codes:\n";
for (const auto& pair : huffmancodes) {
cout << pair.first << ": " << pair.second << endl;
}
// 释放哈夫曼树内存
freehuffmantree(root);
return 0;
}


![[算法] 优选算法(五):二分查找(上)](/images/newimg/nimg3.png)

发表评论