约瑟夫问题（常规代码，递归代码，链表代码）_Python

1.约瑟夫问题：

题目描述

n个人围成一个圈，每个人分别标注为1、2、...、n，要求从1号从1开始报数，报到k的人出圈，接着下一个人又从1开始报数，如此循环，直到只剩最后一个人时，该人即为胜利者。例如当n=10,k=4时，依次出列的人分别为4、8、2、7、3、10，9、1、6、5，则5号位置的人为胜利者。给定n个人，请你编程计算出最后胜利者标号数。

题目输入：

第一行为人数n;
第二行为报数k。

题目输出：

输出最后胜利者的标号数。

2.常规做法题目分析

约瑟夫问题是一个经典的问题，也称为约瑟夫环问题，主要描述的是有一个编号为 1 到 n 的圆圈，从第一个数字开始，按照固定的步长 m 不断地删除最后一个数字，直到圆圈中只剩下一个数字为止，该数字即为胜者。

例如，当 n=7、m=3 时，删除的数字依次为第 3、第 6、第 2、第 7、第 5、第 1 个数字，胜者为第 4 个数字。

数学公式来计算胜者的编号。

假设 n 个人处于圆圈中，编号从 1 到 n。每次删除第 m 个人，直到只剩下一个人为止。

我们可以使用递推的方式来计算胜者的编号。假设 f(n, m) 表示有 n 个人时，每次删除第 m 个人后的胜者编号。

当 n = 1 时，只剩下一个人，编号为 1，即 f(1, m) = 1。

当 n > 1 时，我们可以把约瑟夫问题看作是每次删除第 m 个人，然后从下一个人开始重新编号的问题。所以，当第一个人被删除后，问题变成了有 n-1 个人时，每次删除第 m 个人的约瑟夫问题。此时胜者的编号为 f(n-1, m)。但是，由于每次删除一个人后，编号都会向前移动 m 位，所以原来的第 m 个人的编号变成了新的第 1 个人，即编号为 m 的人成为了新问题的起点。

#include <iostream>

using namespace std;

int josephus(int n, int m) {
    int winner = 0;
    for (int i = 2; i <= n; i++) {
        winner = (winner + m) % i;
    }
    return winner + 1;
}

int main() {
    int n, m;
    cout << "请输入人数 n：";
    cin >> n;
    cout << "请输入步数 m：";
    cin >> m;

    int result = josephus(n, m);

    cout << "胜者的编号是：" << result << endl;

    return 0;
}

3.递归做法题目分析

我们假设约瑟夫问题的递推公式为 f(n,m)，表示有 n 个人时，每数到 m 就删除一个人的情况下，幸存者的编号。那么我们需要推导出 f(n,m) 和 f(n-1,m) 之间的递推关系式。

首先考虑当只有一个人时，即 f(1,m) = 1；

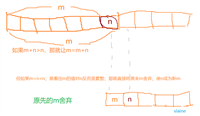
接下来考虑有 n 个人的情况，每次删掉第 m 个人，然后从下一个人开始重新编号，那么就有可能出现这种情况：当删掉第 m 个人后，剩余的 n-1 个人又重新编号为1,2,3,…,n-1。这个时候我们假设当前幸存者的编号为 x，那么显然在去掉第 m 个人之前，幸存者的编号应该为 (x + m - 1) % n + 1，其中 % 表示取模操作。

由此我们可以得到递推公式：f(n, m) = (f(n-1,m) + m - 1) % n + 1。按照这个公式，我们可以依次计算出 f(2,m)、f(3,m)、……、f(n,m) 的值，最终的幸存者的编号就是 f(n,m)。

#include <iostream>
using namespace std;
int f(int a,int b)
{
    if(a==1)
    {
        return 1;
    }
    else
    {
    return (f(a-1,b)+b-1)%a+1;
    }
}
int main()
{
    int n,k;
    cin >> n >> k;
    int result=f(n,k);
    cout << result;
    return 0;
}

4.链表做法题目分析

定义一个循环链表，并将数字 1 到 n 插入其中。
初始化步进变量，从头结点开始遍历链表，删除每 m 个节点。
重复步骤 2 直到链表中只剩下一个节点为止，该节点即为胜者。
使用递归算法来实现步骤 2：在从当前节点开始数第 m 个节点之前，递归地删除前 m-1 个节点。

#include <iostream>
using namespace std;

// 定义链表节点结构体
struct listnode {
    int val;
    listnode *next;
    listnode(int x) : val(x), next(null) {}
};

// 构建一个循环链表
listnode* buildlinkedlist(int n) {
    listnode* head = new listnode(1);
    listnode* prev = head;
    for (int i = 2; i <= n; i++) {
        listnode* node = new listnode(i);
        prev->next = node;
        prev = node;
    }
    prev->next = head; // 将尾节点的 next 指向头节点，形成循环链表
    return head;
}

// 递归删除链表中每 m 个节点之前的前 m-1 个节点
listnode* deletekth(listnode* cur, int m) {
    // 如果链表只剩一个节点，返回该节点
    if (cur->next == cur) return cur;

    // 找到当前节点的前 m-1 个节点
    for (int i = 0; i < m - 2; i++) {
        cur = cur->next;
    }

    // 删除第 m 个节点，并将链表尾部连接到下一个节点
    listnode* next = cur->next->next;
    delete cur->next;
    cur->next = next;

    // 递归删除下一个节点之前的前 m-1 个节点
    return deletekth(next, m);
}

int josephus(int n, int m) {
    listnode* head = buildlinkedlist(n);

    // 使用递归算法删除节点
    listnode* winner = deletekth(head, m);

    int ans = winner->val;
    delete winner;

    return ans;  // 返回胜者的编号
}

int main() {
    int n, m;
    cin >> n >> m;

    int ans = josephus(n, m);

    cout << ans << endl;

    return 0;
}