我要评论这篇文章主要是讲的python语言的算法，本人还在不断记笔记中，文章也会持续更新，内容比较浅薄，请大家指教
另外推荐一个比较好用的记笔记的软件typora,自己已经使用很久了，感觉不错。。。虽然但是还是有欠缺。
目录
2.2.1链表的基本操作（忽略查找过程插入删除操作时间复杂度都是o（1））
2.队列通常是对历史的回忆，正序（多线程和争夺公平锁，网络爬取url）
第一章 算法概述
1.1 什么是数据结构？
01 数据结构都有哪些组成方式
-
线性结构 最简单的数据结构（数组 链表 栈 队列 哈希表）
-
树 （二叉树 二叉堆）
-
图（多对多的关联关系）
-
跳表 哈希链表 位图.....
02 时间复杂度
设t(n)为程序基本执行次数的函数（程序的相对执行时间函数），n为输入规模，以下是程序中常见的四种执行方式：
例01 渐进时间复杂度
若存在函数f(n)，使得当n趋近于无穷大时，t(n)/f(n)的极限值为不等于零的常数，则称f(in)是t(n)的同数量级函数。记作t(n)= o(f(n))，称为o(f(n))，0为算法的渐进时间复杂度，简称为时间复杂度。
如何推导出时间复杂度呢?有如下几个原则:
-
如果运行时间是常数量级，则用常数1表示
-
只保留时间函数中的最高阶项。
-
如果最高阶项存在，则省去最高阶项前面的系数。
03 空间复杂度:s(n) = o(f(n))
1.常量空间 o(1)
2.线性空间 o(n)
3.三维空间：当算法分配的空间是一个二维列表集合，并且集合的长度和宽度都与输入规模n成正比时，空间复杂度记作o(n^2)
4.递归空间：函数调用栈（进栈和出栈）其算法的空间复杂度和递归深度成正比
第二章 数据结构基础
2.1 数组的基本操作 （读取 更新 插入 删除）
$$
数组多适合的是读操作多，写操作少的场景 数组是顺序存储
$$
数组多适合的是读操作多，写操作少的场景 数组是顺序存储
数组读取元素和更新元素的时间复杂度都是o(1)
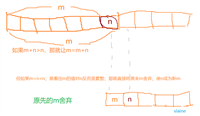
在初始化列表时已经确定了数组的长度，所以要想实现超范围插入则涉及到数组的扩容
例01 插入：
'''
# 初始化列表
my_list = [6,1,5,4,2,7,8,9,3]
# 读取列表
print(my_list[2])
'''
# 插入算法
class myarray:
def __init__(self,capacity):
self.array = [none] * capacity
self.size = 0
def insert(self,index,element):
# 判断访问下标是否超出范围
if index < 0 or index > self.size:
raise exception("超出数组实际元素范围！")
# 从右向左循环，逐个向右挪动一位
for i in range(self.size - 1,-1,-1):#从大到小遍历一个序列
self.array[i+1] = self.array[i]
# 腾出的位置放置新元素
self.array[index] = element
self.size += 1
def output(self):
for i in range(self.size):
print(self.array[i])
array =
发表评论