3D Gaussian Splatting介绍

一、概述

3d gaussian splatting和nerf一样，主要用于新视图合成。
特点：

• 使用光栅化渲染方式，而不是nerf的基于射线的体渲染（volumetric rendering along a ray）
• 使用多个3d高斯球显示的表达场景
• 训练推理速度快的同时保证质量高
• 本质上是一个优化问题，没有使用神经网络

二、基础介绍

1. 多维高斯分布

gaussians are defined by a full 3d covariance matrix σ defined in world space centered at point (mean) $\mu$

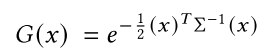
进行了一定简化，我们回顾一下原始形式，若随机变量服从$x\sim n(\mu ,{\sigma }^2)$,则有如下的概率密度函数

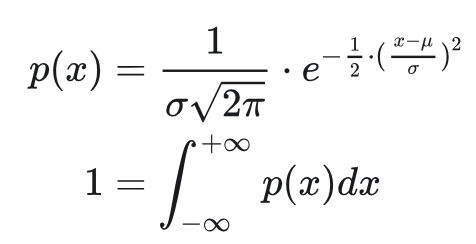
对应到多元，就是下面的形式，

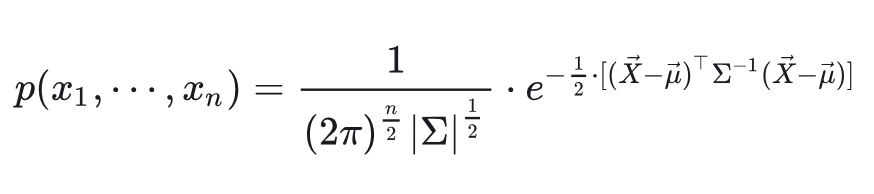
高斯分布的协方差σ 是正定矩阵，一定可以进行对角化，因此可以分解成如下形式

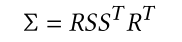
r通过四元数表示，4个参数，s为对角矩阵，3个参数，所以协方差一共7个参数

2. 将3d 高斯投影到2d像素平面

$$y=p_c=w_w^c{p}_w+t_w^c$$
线性变换，依然符合高斯分布
$${\sigma }_{p_c}=w{\sigma }_{p_w}{w}^t$$
从相机坐标系变换到像素坐标系：
z = [ z x z y 1 ] = ( 1 / p c z ) [ f x 0 c x 0 f y c y 0 0 1 ] [ p c x p c y p c z ] z = \begin{bmatrix} z_x\\ z_y\\ 1 \end{bmatrix}=(1/p_c^z)\begin{bmatrix} fx& 0& cx& \\ 0& fy& cy& \\ 0& 0& 1& \end{bmatrix} \begin{bmatrix} p_c^x\\ p_c^y\\ p_c^z \end{bmatrix} z= ​zx​zy​1​ ​=(1/pcz​) ​fx00​0fy0​cxcy1​​ ​ ​pcx​pcy​pcz​​ ​
这个变换是非线性的，需要进行一阶泰勒展开，$z=f(p_c)\approx f({\mu }_y)+j(y-{\mu }_y)$,进而得到协方差变换为：
$${\sigma }_z=j{\sigma }_{p_c}{j}^t=jw{\sigma }_{p_w}{w}^t{j}^t$$
均值如下：
$${\mu }_z=f({\mu }^y)=f(w{\mu }_{p_w^c}+t)$$

3. 球谐函数

• 球谐函数用于表达空间中某点的光照模型（nerf通过mlp来建模光照模型，输入(x,y,z,theta,phi)-> mlp->颜色c）
• 光照函数$c(\theta ,\varphi )$可以表示为球谐函数的加权线性组合，如下，某一个位置高斯球的函数，输入为角度，输出为这个角度的颜色
  
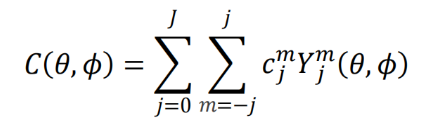
  其中：
  
• m由j决定，如j=3, m=-3,-2,-1,0,1,2,3, j =2 m = -2,-1,0,1,2 , 对应7+5+3+1=16个球谐函数，所以有16个系数c,rgb分别对应一个球谐函数线性组合，所以光照模型一共16*3=48个参数，这些参数就是需要优化的变量。
• 输入$(\theta ,\varphi )$，确定j,那么球谐函数就是固定的，如下，带入$(\theta ,\varphi )$，那么球谐函数就是一个个实数
  
  带入j,化简之后：
  
  其他如下图所示
  
  实际使用时，不用$(\theta ,\varphi )$，而是使用方向向量d = (x,y,z)（模长为1），转换如下图所示，这样就可以把上面球谐函数表示为关于x,y,z的函数。
  

nerf通过mlp确定光照模型，这里是通过球谐函数确定光照模型，每个高斯球48个参数，估计出来就能知道这个高斯球的光照模型。

注：也可以理解为一种朝向编码方法，nerf中姿态会进行编码，这种编码方式可以替换为球谐函数，更有物理意义。

4. splatting and $\alpha$ blending

splatting是一种光栅化（rasterize）3d对象的方法，即将3d对象投影到2d图形。如将3d高斯球（也可以是其他图形）往像素平面扔雪球，在像素平面的能量从中心向外扩散并减弱。该过程可以方便的并行处理。一会可以看到，这对应后面的projection过程，即把3d高斯球投影到2d图像上的过程。
$\alpha$ blending介绍
光栅化之后怎么混合这些像素平面的椭球呢？使用$\alpha$ blending，主要解决图层融合的问题。
以两幅图像为例，图像$i_1$透明度为katex parse error: undefined control sequence: \lapha at position 1: \̲l̲a̲p̲h̲a̲_1,图像$i_{bk}$为背景，融合公式如下：
$$i_{result}=i_1\ast {\alpha }_1+i_{bk}\ast (1-{\alpha }_1)$$

扩展到多张图，按照深度由近到远排序四张图，融合公式如下：$i_{bk}$先和$i_3$融合，再和$i_2$,$i_1$

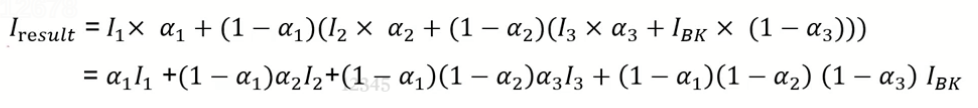
$i_{bk}$为0，则可以写成

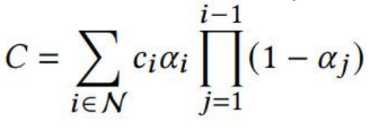
这就是$\alpha$ blending 公式了。

接下来说一下$\alpha$ blending和nerf体渲染的区别：
体渲染公式如下：


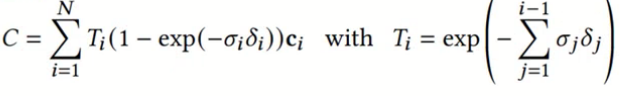
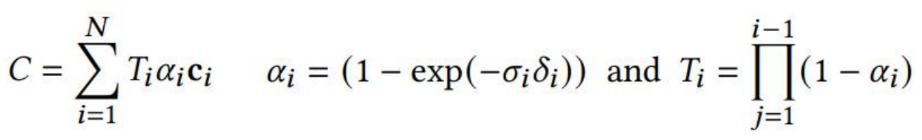
公式相同，虽然公式相同，但实现上区别比较大，应用方式也不一样。

三、整体流程

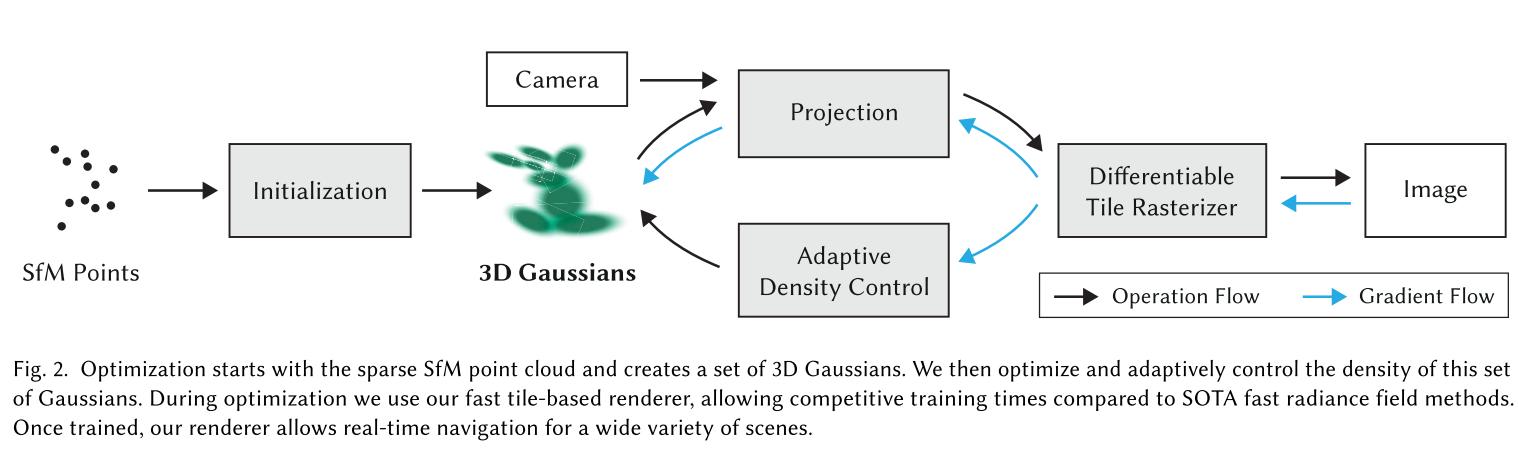
场景表达通过很多个高斯球来实现，如下图所示，每个高斯球对应59个参数。

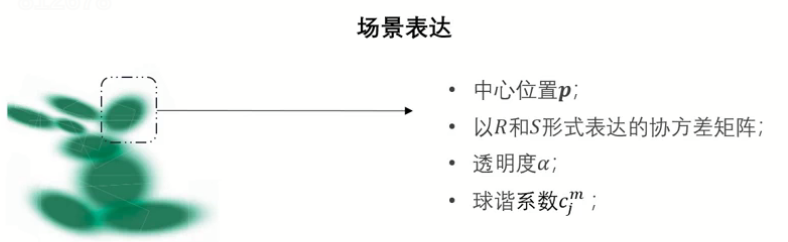
其中决定一个高斯球需要59个系数来表达，这些也是优化问题要求解的状态：

• 中心位置：3dof
• 协方差矩阵：7dof
• 透明度：1dof
• 球谐系数：48 dof(j = 3，16 * 3)

整体流程

1）initialization: 输入为3d点云，可以 通过colmap得到，(nerf也会用到colmap，使用位姿), 基于这些点云初始化高斯球，每个点云位置放置一个高斯球，中心点位置设置为点云位置，其他随机初始化
2) projection: 根据相机内外参数（图像位姿），把高斯球splatting到图像上–把能看到99%的所有高斯球投影到图像上（参考“将3d 高斯投影到2d像素平面”）使用下面3个公式

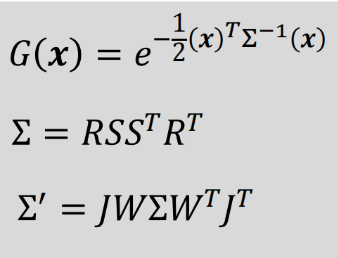
3）differentiable tile rasterizer：在投影重叠区域进行光栅化渲染（differentiable tile rasterizer），使用$\alpha$ blending，这是确定的函数，不需要学习。把这些高斯球进行混合，过程可微，公式就是：

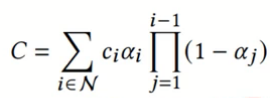
4）与gt计算loss，更新每个高斯球的59维系数

损失函数为：

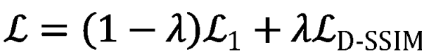
其中：

• l1 loss：基于逐像素比较差异，然后取绝对值
  
• ssim loss（结构相似）损失函数：考虑了亮度 (luminance)、对比度 (contrast) 和结构 (structure)指标，这就考虑了人类视觉感知，一般而言，ssim得到的结果会比l1，l2的结果更有细节，ssim 的取值范围为 -1 到 1，1 表示两幅图像完全一样，-1 表示两幅图像差异最大。
  

def _ssim(img1, img2, window, window_size, channel, size_average=true):
    mu1 = f.conv2d(img1, window, padding=window_size // 2, groups=channel)
    mu2 = f.conv2d(img2, window, padding=window_size // 2, groups=channel)

    mu1_sq = mu1.pow(2)
    mu2_sq = mu2.pow(2)
    mu1_mu2 = mu1 * mu2

    sigma1_sq = f.conv2d(img1 * img1, window, padding=window_size // 2, groups=channel) - mu1_sq
    sigma2_sq = f.conv2d(img2 * img2, window, padding=window_size // 2, groups=channel) - mu2_sq
    sigma12 = f.conv2d(img1 * img2, window, padding=window_size // 2, groups=channel) - mu1_mu2

    c1 = 0.01 ** 2
    c2 = 0.03 ** 2

    ssim_map = ((2 * mu1_mu2 + c1) * (2 * sigma12 + c2)) / ((mu1_sq + mu2_sq + c1) * (sigma1_sq + sigma2_sq + c2))

    if size_average:
        return ssim_map.mean()
    else:
        return ssim_map.mean(1).mean(1).mean(1)

参考论文：loss functions for image restoration with neural networks（）
参考链接：wiki

5）梯度回传

• 更新每个高斯球的属性（59维系数）-这是个优化问题
  
• adaptive density control：根据梯度实现3d高斯球的clone和split,具体而言

1. 学习过程中，较大梯度（59维导数，模长大）的高斯球存在under-reconstruction和over-reconstruction问题
2. under-reconstruction区域的高斯球方差小，进行clone
3. over-reconstruction区域高斯球方差大，进行split
   
4. 每经过固定次数的迭代进行一次剔除操作，剔除几乎透明（透明度接近0）的高斯球以及方差过大的高斯球

四、 伪代码

对应colmap输入点云，内部处理流程：

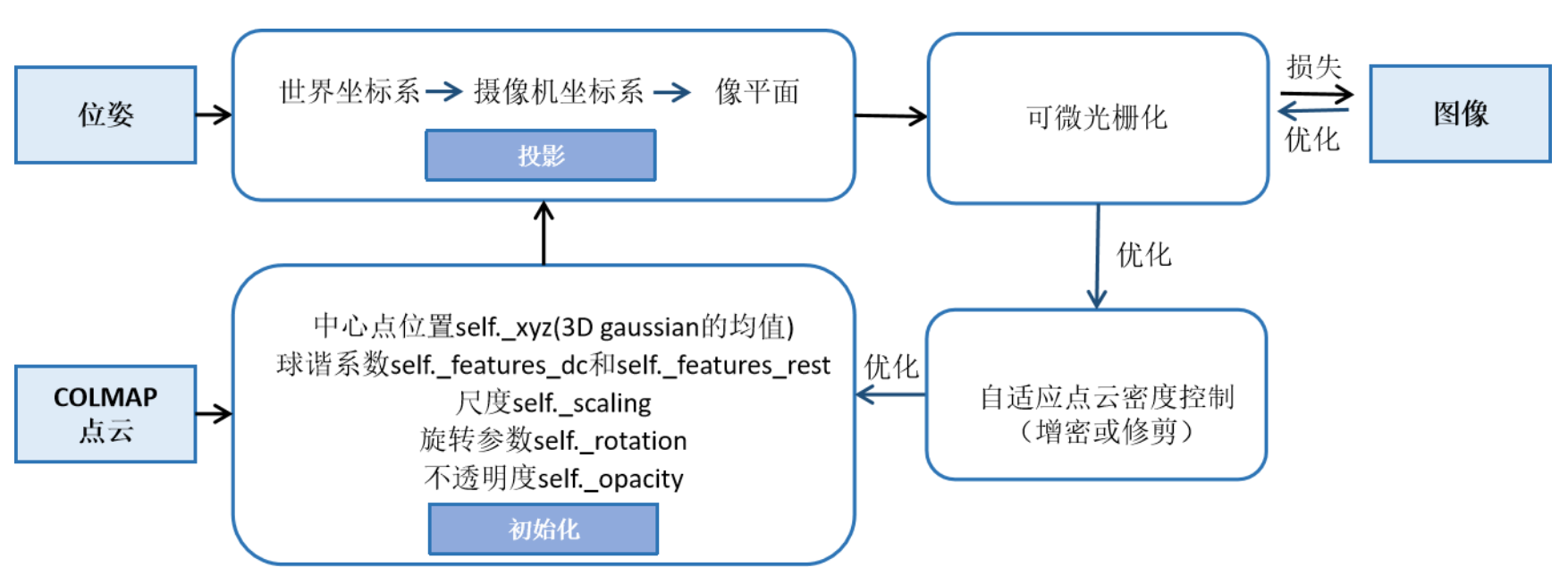
rasterization pipeline：

1. cull some 3d gaussian, 99%必须投影到当前图像，才有效
   2）都投影到图像
   3）把图像分成很多tile,并行处理
   4）建立索引和tile的对应关系，每个tile的深度值存在key里面
   5）key排序
   6）逐个tile渲染
   注意：rasterzation时，每个高斯球投影到image时，透明度也需要从中心点开始递减，根据概率衰减

五、评价指标

psnr (peak signal-to-noise ratio) 峰值信噪比是一种评估图像质量的常用指标，主要用于衡量原始图像和压缩或重构后的图像之间的质量差异。

• psnr 是基于预测错误的均方值来定义的，公式为：
• 

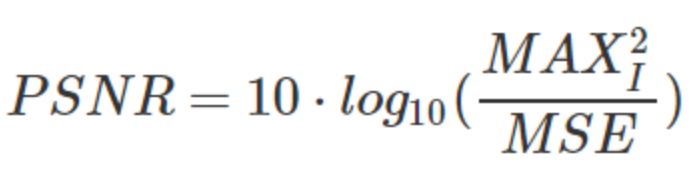
其中，max_i 是图像可能的最大像素值（对于8位图像来说，值为255），mse 是均方误差，计算公式为：

• mse = (1/mn) σσ[(i(i,j)-k(i,j))^2] (i=1:m, j=1:n)

其中，i(i,j) 和 k(i,j) 分别是在位置 (i,j) 的原始图像和重构后的图像单元像素的亮度值，‘m’ 和 ‘n’ 分别是图像的行数和列数。
psnr 的取值范围是 0到无穷大，单位是 db(分贝)。psnr 值越大，说明重构图像质量越高。但需要注意的是，psnr 只是一个粗略的图像质量度量指标，有时候 psnr 很高的两幅图像，人眼可能会觉得差异很大；反之，psnr 很低的两幅图像，人眼可能觉得差异不大。

六、实验结果

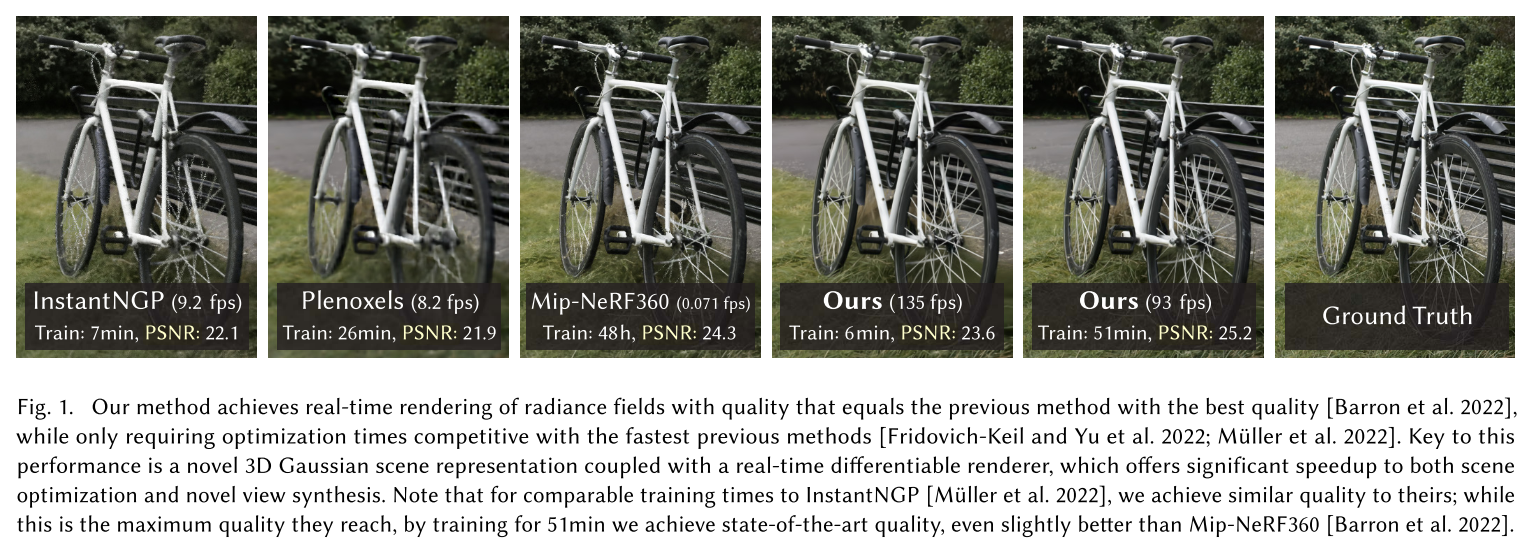
训练速度快，和instant ngp相当，效果更好。推理速度135fps,很快，训练时间增长51min，效果比mip-nerf360更好，因为有更多高斯球，所以推理速度慢一点，但也有93fps.

七、reference

多元高斯分布介绍
深蓝学院课程