等差数列划分

思路:
- 经验+题目要求
dp[i]表示:以 i 位置为结尾的所有子数组中有多少个等差数列
- 状态转移方程
对 dp[i] 位置,数列至少有三个元素,如果相邻三个为等差数列,dp[i] = dp[i-1] + 1;
如果相邻三个不为等差数列,dp[i] = 0;
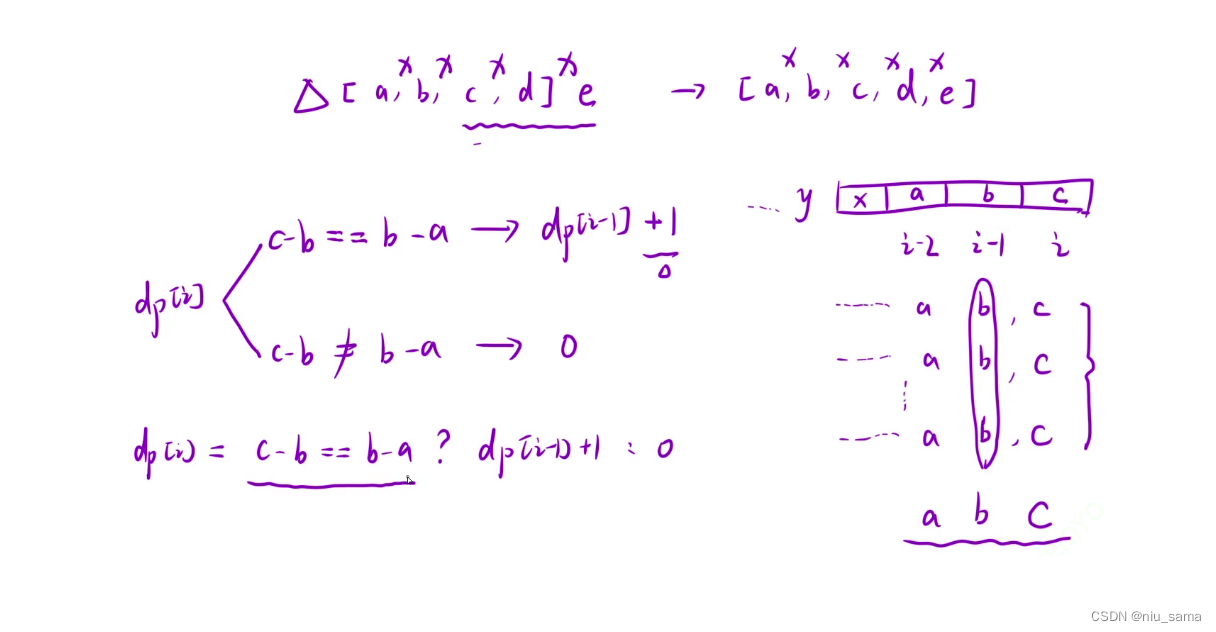
- 初始化
dp[0] 和 dp[1] 位置都不符合判断要求,直接 dp[0] = dp[1] = 0;
- 填表顺序
从左往右,返回表里所有的和。
class solution {
public:
int numberofarithmeticslices(vector<int>& nums) {
int n = nums.size();
vector<int> dp(n);
int count = 0;
for(int i = 2; i<n; i++)
{
if(nums[i]-nums[i-1] == nums[i-1]-nums[i-2])
dp[i] = dp[i-1]+1;
else
dp[i] = 0;
count+=dp[i];
}
return count;
}
};
最长湍流子数组

像这样一升一降的就叫湍流子数组。
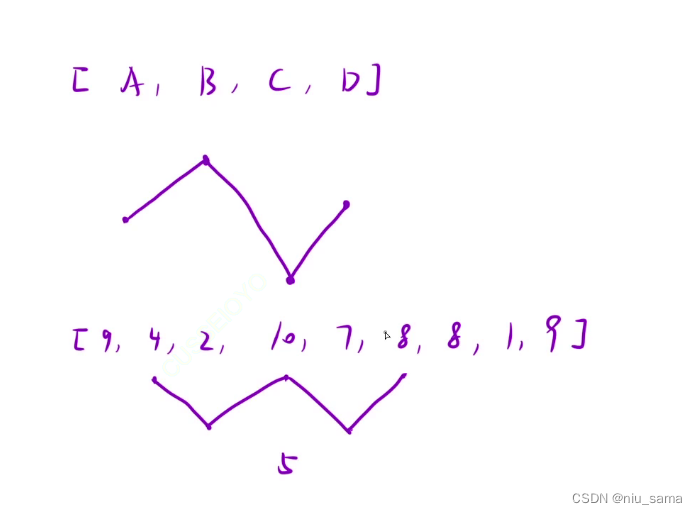
思路:
1.经验+题目要求
dp[i]表示:以 i 位置为结尾的所有子数组中,最长湍流子数组的长度。
对于本题,如果只定一个状态数组是不够的,因为我们只有区分了 i 位置是在增长还是在降低,才能判断 i + 1 位置是否能续上前面的波浪。所以,我们需要定义两个状态数组,分别表示以 i 结尾的在增长和降低的最长湍流子数组长度。
f[i] 表示:以i 位置为结尾的所有子数组中,最后呈现 “ 上升” 状态下的最长湍流数组的长度。
g[i] 表示:以i 位置为结尾的所有子数组中,最后呈现 “ 下降” 状态下的最长湍流数组的长度。
2.状态转移方程
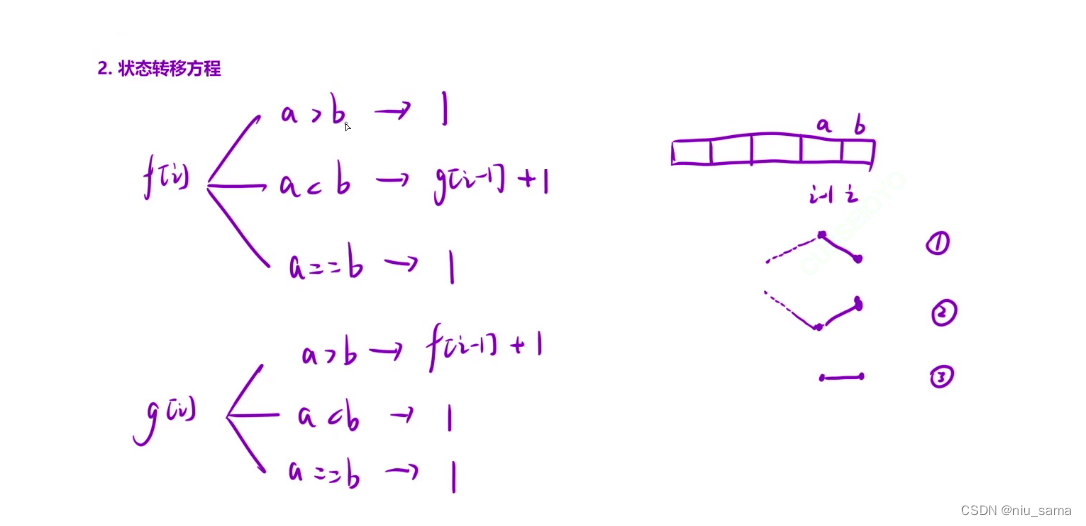
- 初始化
单个 存在为1,直接初始化全为1。
- 填表
从左往右,两个表一起填写。
class solution {
public:
int maxturbulencesize(vector<int>& arr) {
int n = arr.size();
vector<int> f(n,1);
auto g = f;
int ret = 1;//最差情况是1,ret写为1;
for(int i = 1; i<n; i++)
{
if(arr[i] > arr[i-1])
{
f[i] = g[i-1] + 1;
ret = max(ret,f[i]);
}
else if(arr[i] < arr[i-1])
{
g[i] = f[i-1] + 1;
ret = max(ret,g[i]);
}
}
return ret;
}
};
环绕字符串中唯一的子字符串

思路:
- 经验+题目要求
dp[i]表示:以 i 位置为结尾的所有字串中,有多少个在 base 中出现过。
- 状态转移方程
如果长度为1,就是本身字符串为1;
长度大于1:就要看s[i-1] + 1是否等于s[i] ;(特殊情况是“za”的情况)
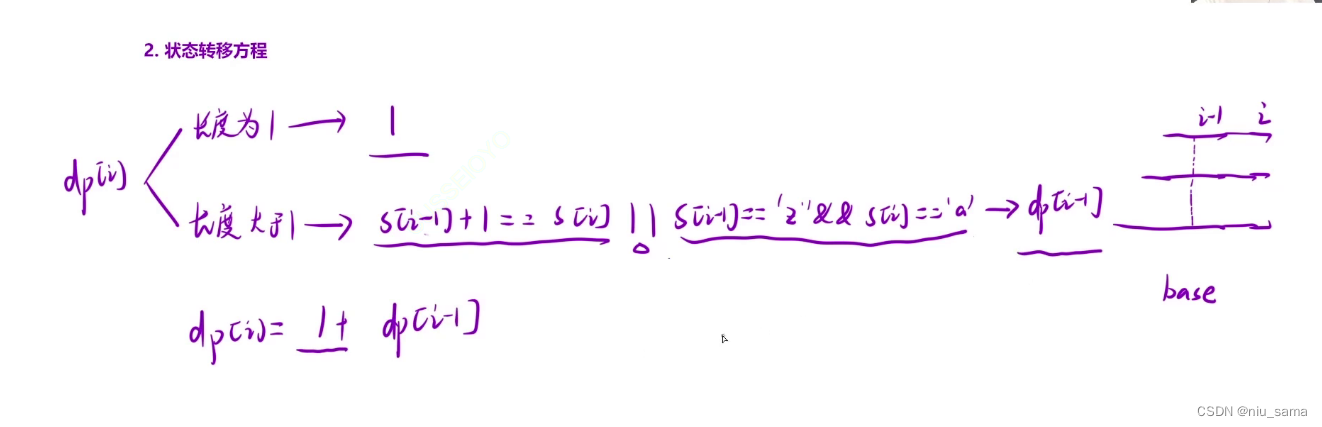
- 初始化
dp 表里面所有的值都初始化为1。因为每一个本身字符都在base中出现过。
- 填表
从左往右填表
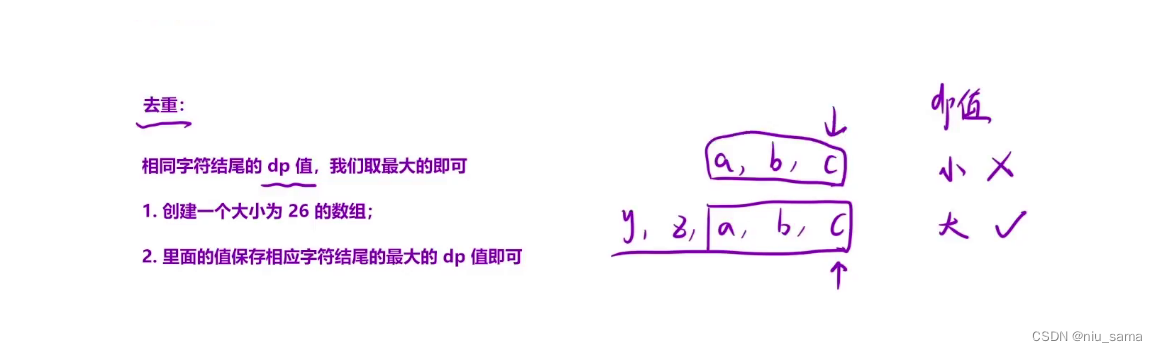
去重操作:
对于右边的例子,abc 在 yzabc,zabc都出现过,我们直接取以c结尾的最大的dp值就可以。
class solution {
public:
int findsubstringinwraproundstring(string s) {
int n = s.size();
vector<int> dp(n,1);
for(int i = 1; i<n; i++)
{
if(s[i-1] + 1 == s[i] || (s[i-1] == 'z' && s[i] == 'a'))
dp[i] = dp[i-1] + 1;
}
int hash[26] = {0};
for(int i = 0; i<n; i++)
{
hash[s[i] - 'a'] = max(hash[s[i]-'a'],dp[i]);
}
int sum = 0;
for(auto x : hash) sum+=x;
return sum;
}
};
最长递增子序列

注意:这里的子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
思路:
- 经验+题目要求
dp[i]表示:以 i 位置为结尾的所有子序列中,最长递增子序列的长度。
- 状态转移方程
如果长度为1,就为1;
长度大于1,就要找nums[i] 大于 nums(0,j)里面的子序列,大于的话就为dp[i] = dp[j] + 1;
然后每一次找到dp[i] 里面的最大值并记录。
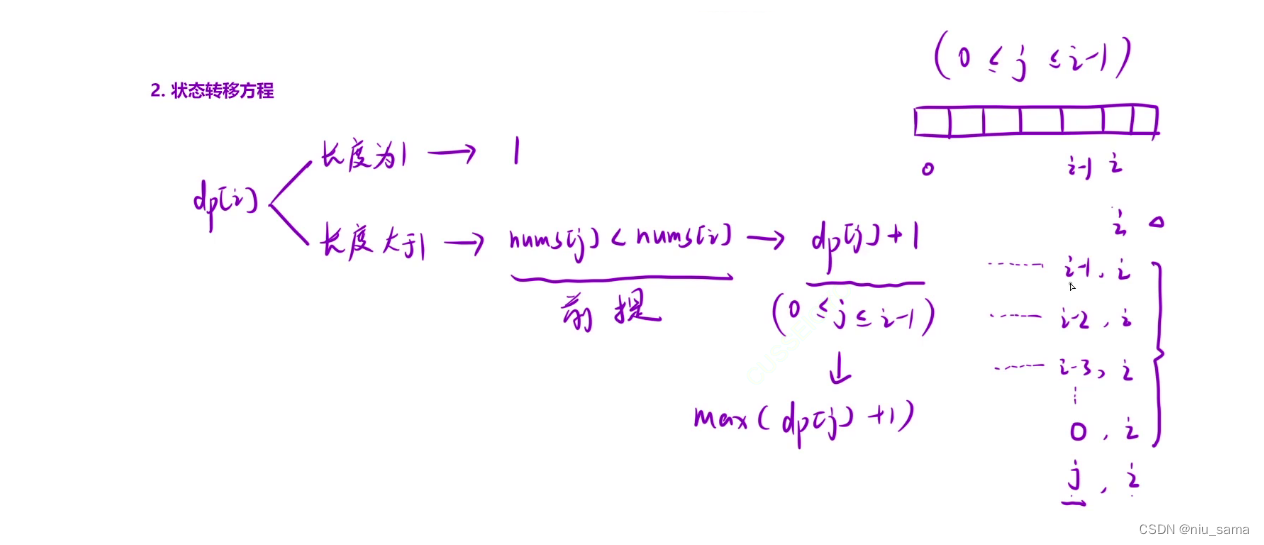
- 初始化
全部初始化为1,因为长度为1,dp[i] 为1.
- 填表
从左往右填表:
class solution {
public:
int lengthoflis(vector<int>& nums) {
int n = nums.size();
vector<int> dp(n,1);
int ret = 1;
for(int i = 1; i<n; i++)
{
for(int j = 0; j<i; j++)
{
if(nums[i] > nums[j])
{
dp[i] = max(dp[j] + 1,dp[i]);
}
ret = max(ret,dp[i]);
}
}
return ret;
}
};





发表评论