第九章 动态规划part11

最长公共子序列

题目描述

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

• 例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。

两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

示例 1：

输入：text1 = "abcde", text2 = "ace" 
输出：3  
解释：最长公共子序列是 "ace" ，它的长度为 3 。

示例 2：

输入：text1 = "abc", text2 = "abc"
输出：3
解释：最长公共子序列是 "abc" ，它的长度为 3 。

示例 3：

输入：text1 = "abc", text2 = "def"
输出：0
解释：两个字符串没有公共子序列，返回 0 。

解题思路

1. 确定dp数组以及下标的含义

   • dp[i][j]代表着text1的前i个字符(即text1[0]到text1[i-1])与text2的前j个字符(即text2[0]到text2[j-1])的最长公共子序列的长度

2. 确定递推公式

   • 对于dp[i][j]，如果text1[i-1] == text2[j-1]，则说明我们可以在前i-1个字符与前j-1个字符的最长公共子序列的基础上，再加上一个公共字符，因此，递推公式为：dp[i][j] = dp[i-1][j-1] + 1；
   • 如果text1[i-1] != text2[j-1]，则说明当前字符并不公共，那么最长公共子序列就只能是从text1的前i-1个字符与text2的前j个字符的最长公共子序列，和text1的前i个字符与text2的前j-1个字符的最长公共子序列中选取最长的那一个，因此，递推公式为：dp[i][j] = max(dp[i-1][j], dp[i][j-1])。

3. dp数组初始化

   • 将dp数组的所有元素初始化为0。这样做主要是因为当text1或text2为空字符串，即长度为0时，它们与任何字符串的最长公共子序列的长度都为0。

4. 确定遍历顺序

   • 由于dp[i][j]的值是基于dp[i-1][j-1]、dp[i-1][j]和dp[i][j-1]的值来计算的，所以我们需要从左至右，从上至下的顺序来遍历数组，这样才能保证在计算dp[i][j]时，dp[i-1][j-1]、dp[i-1][j]和dp[i][j-1]的值已经被计算并更新。

5. 举例推导dp数组

   • 以输入：text1 = “abcde”, text2 = “ace” 为例，手推dp数组状态图：

     

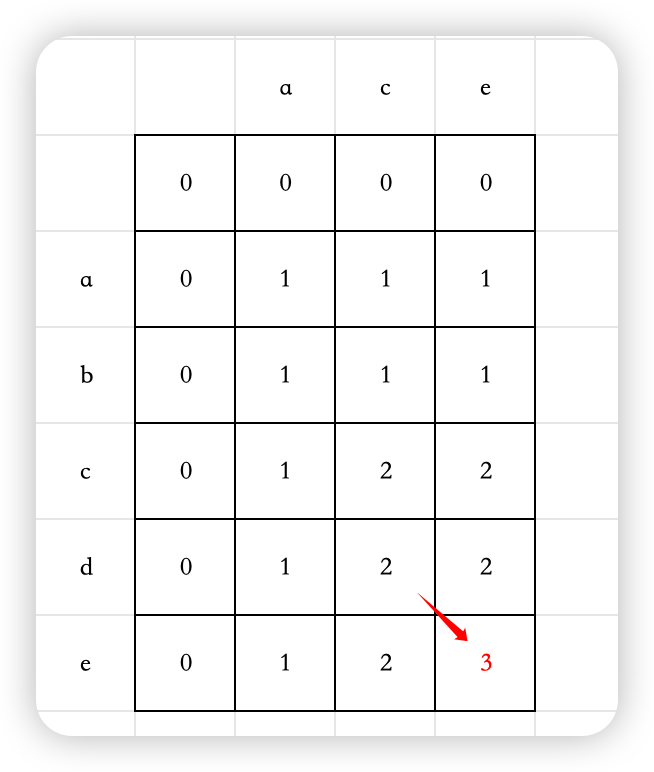
代码实现

测试地址：https://leetcode.cn/problems/longest-common-subsequence/

class solution {
public:
    int longestcommonsubsequence(string text1, string text2) {
        // 初始化dp数组，其维度为(text1的长度+1) x (text2的长度+1)，所有元素初始值为0
        vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));
        // 遍历两个字符串的每个字符
        for (int i = 1; i <= text1.size(); i++) {
            for (int j = 1; j <= text2.size(); j++) {
                // 如果当前字符匹配
                if (text1[i - 1] == text2[j - 1]) {
                    // 更新dp数组，当前匹配字符的最长公共子序列长度为左上角元素的值加1
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }
                // 如果当前字符不匹配
                else {
                    // 更新dp数组，当前最长公共子序列长度为左边或上边元素的最大值
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        // 返回dp数组右下角的值，即为最长公共子序列的长度
        return dp[text1.size()][text2.size()];
    }
};

不相交的线

题目描述

在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。

现在，可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，这些直线需要同时满足：

• nums1[i] == nums2[j]
• 且绘制的直线不与任何其他连线（非水平线）相交。

请注意，连线即使在端点也不能相交：每个数字只能属于一条连线。

以这种方法绘制线条，并返回可以绘制的最大连线数。

示例 1：

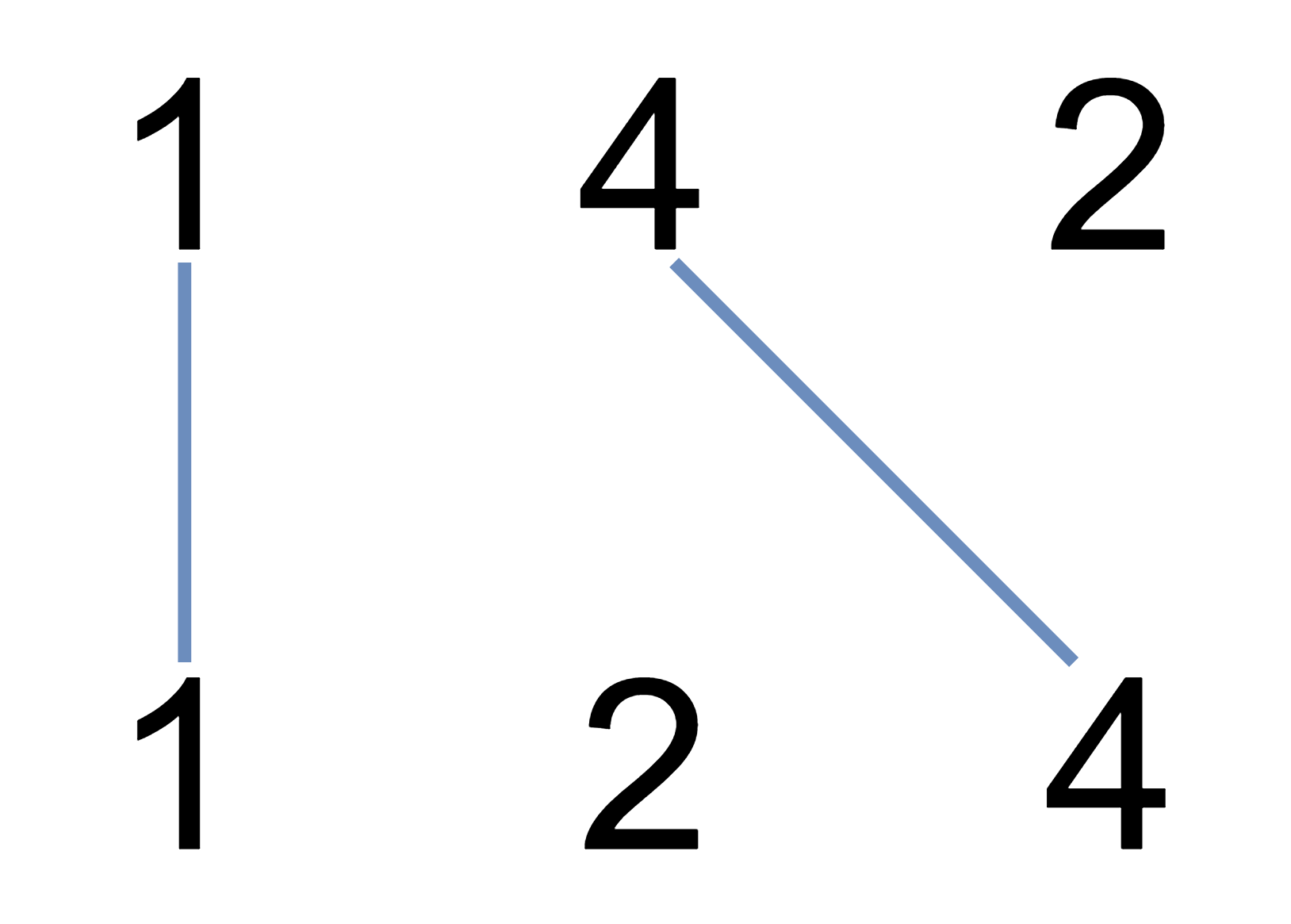
输入：nums1 = [1,4,2], nums2 = [1,2,4]
输出：2
解释：可以画出两条不交叉的线，如上图所示。 
但无法画出第三条不相交的直线，因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。

示例 2：

输入：nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2]
输出：3

示例 3：

输入：nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1]
输出：2

解题思路

本题的要求是找出在两个数组nums1和nums2之间可以画出的最多未交叉线的数量。这个问题可以转化为找到两个数组的((20240716161724-fh0j0sj “最长公共子序列”))（lcs）问题，因为每个匹配的元素都代表着一条未交叉的线，而未交叉的线集合最大化的问题等同于最大化两个数组中匹配元素对的数量。

代码实现

测试地址：https://leetcode.cn/problems/uncrossed-lines/

class solution {
public:
    int maxuncrossedlines(vector<int> &nums1, vector<int> &nums2) {
        // 创建一个二维dp数组，用于存储解决子问题的结果
        vector<vector<int>> dp(nums1.size() + 1, vector<int>(nums2.size() + 1, 0));
    
        // 遍历nums1和nums2中的每个数字
        for (int i = 1; i <= nums1.size(); i++) {
            for (int j = 1; j <= nums2.size(); j++) {
                // 如果当前nums1和nums2中的元素相同，则增加未交叉线的数量
                if (nums1[i - 1] == nums2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }
                // 如果不同，则取两种情况的较大值，不增加线的数量
                else {
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        // 返回整个表格的最后一个元素，这是两个数组间最多未交叉线的数量
        return dp[nums1.size()][nums2.size()];
    }
};

最大子数组和

题目描述

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

示例 2：

输入：nums = [1]
输出：1

示例 3：

输入：nums = [5,4,-1,7,8]
输出：23

解题思路

1. 确定dp数组以及下标的含义

   • dp[i]表示的是以nums[i]结尾的最大子序和

2. 确定递推公式

   • dp[i]可以继续加上nums[i]延长子序列，或者以nums[i]重新开始一个新的子序列，因此递推公式为：max(dp[i - 1] + nums[i], nums[i]);

3. dp数组初始化

   • dp[0] = nums[0]，即以nums[0]结尾的最大子序和就是nums[0]本身。

4. 确定遍历顺序

   • 对于dp[i]，其值与dp[i-1]有关，因此需要保证dp[i-1]在dp[i]之前被计算。所以，遍历顺序应该是从左到右。

5. 举例推导dp数组

   • 以示例一为例，输入：nums = [-2,1,-3,4,-1,2,1,-5,4]，手推dp数组状态图如下：

     

代码实现

测试地址：https://leetcode.cn/problems/maximum-subarray/

class solution {
public:
    int maxsubarray(vector<int> &nums) {
        // 创建一个一维dp数组，用于存储解决子问题的结果
        vector<int> dp(nums.size(), 0);
    
        // 初始化dp数组的第一个元素
        dp[0] = nums[0];
    
        // 初始化最大子序和为数组的第一个元素
        int ans = dp[0];
    
        // 遍历nums中的每个数字，从第二个元素开始
        for (int i = 1; i < nums.size(); i++) {
            // 计算以当前元素结尾的最大子序和
            dp[i] = max(dp[i - 1] + nums[i], nums[i]);
        
            // 更新全局最大子序和
            ans = max(ans, dp[i]);
        }
    
        // 返回全局最大子序和
        return ans;
    }
};

判断子序列

题目描述

给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。

进阶：

如果有大量输入的 s，称作 s1, s2, … , sk 其中 k >= 10亿，你需要依次检查它们是否为 t 的子序列。在这种情况下，你会怎样改变代码？

示例 1：

输入：s = "abc", t = "ahbgdc"
输出：true

示例 2：

输入：s = "axc", t = "ahbgdc"
输出：false

解题思路

虽然本题是判断 s 是否为 t 的子序列，这可以视为一种特殊的((20240716161724-fh0j0sj “最长公共子序列”))问题，即lcs的长度是否等于 s 的长度。如果等于，说明 s 的每个字符都按顺序在 t 中出现，即 s 是 t 的子序列。

代码实现

测试地址：https://leetcode.cn/problems/is-subsequence/

class solution {
public:
    bool issubsequence(string s, string t) {
        // 创建一个二维dp数组，用于存储中间结果，dp[i][j] 表示s的前i个字符与t的前j个字符的最长公共子序列长度
        vector<vector<int>> dp(s.size() + 1, vector<int>(t.size() + 1, 0));
    
        // 遍历字符串s和t
        for (int i = 1; i <= s.size(); i++) {
            for (int j = 1; j <= t.size(); j++) {
                // 如果当前字符相等，当前最长公共子序列长度为前一个状态加一
                if (s[i - 1] == t[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }
                // 如果当前字符不相等，维持与前一状态相同的长度
                else {
                    dp[i][j] = dp[i][j - 1];
                }
            }
        }
    
        // 检查s的长度是否等于在t中找到的最长公共子序列长度
        return dp[s.size()][t.size()] == s.size();
    }
};