一些结论
文心一言4.0 vs chatgpt plus横向对比
文心一言4.0价格
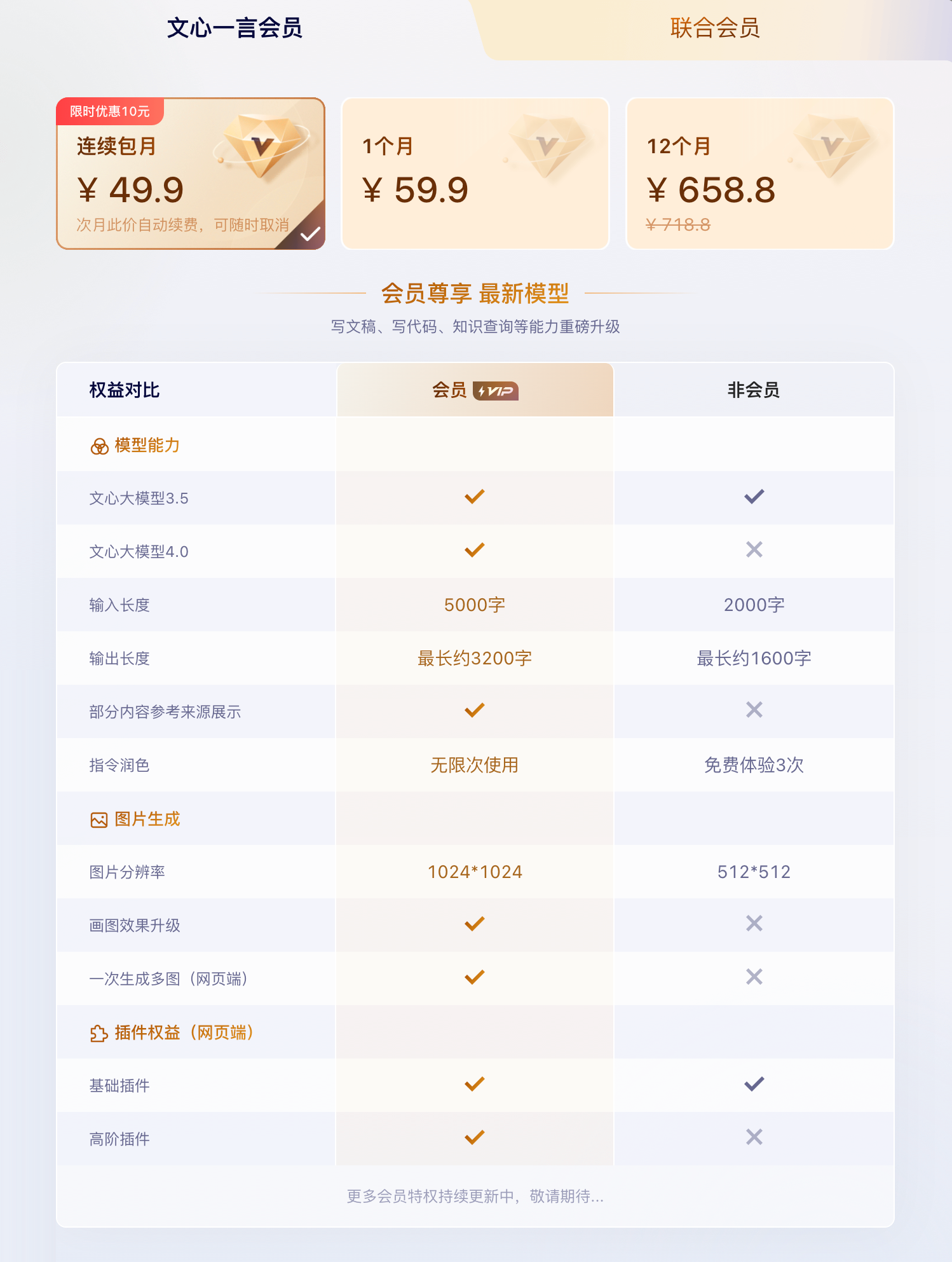
文心一言4.0使用数量限制

文心一言4.0 vs 文心一言3.5(官方宣传版)

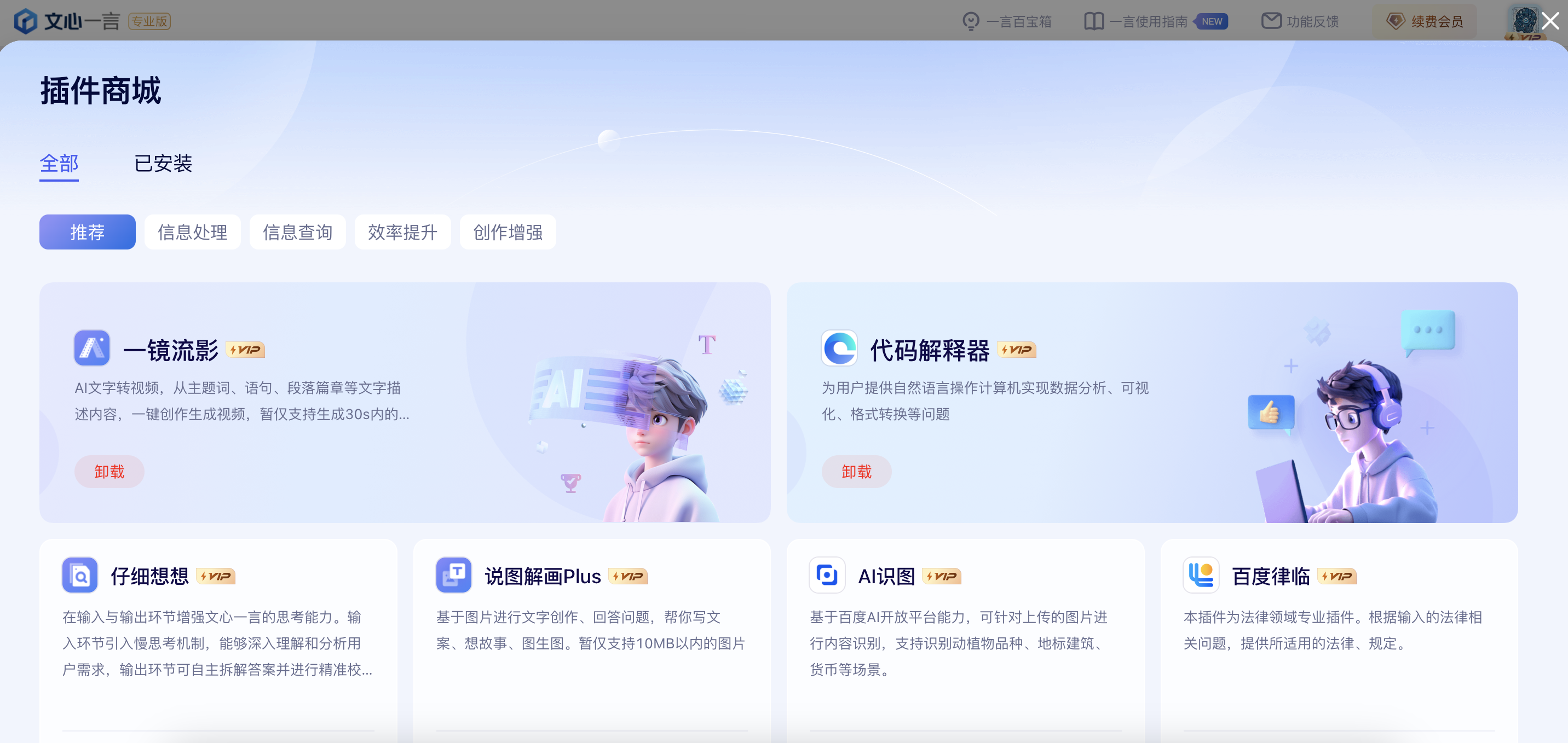
文心一言4.0会员专属插件
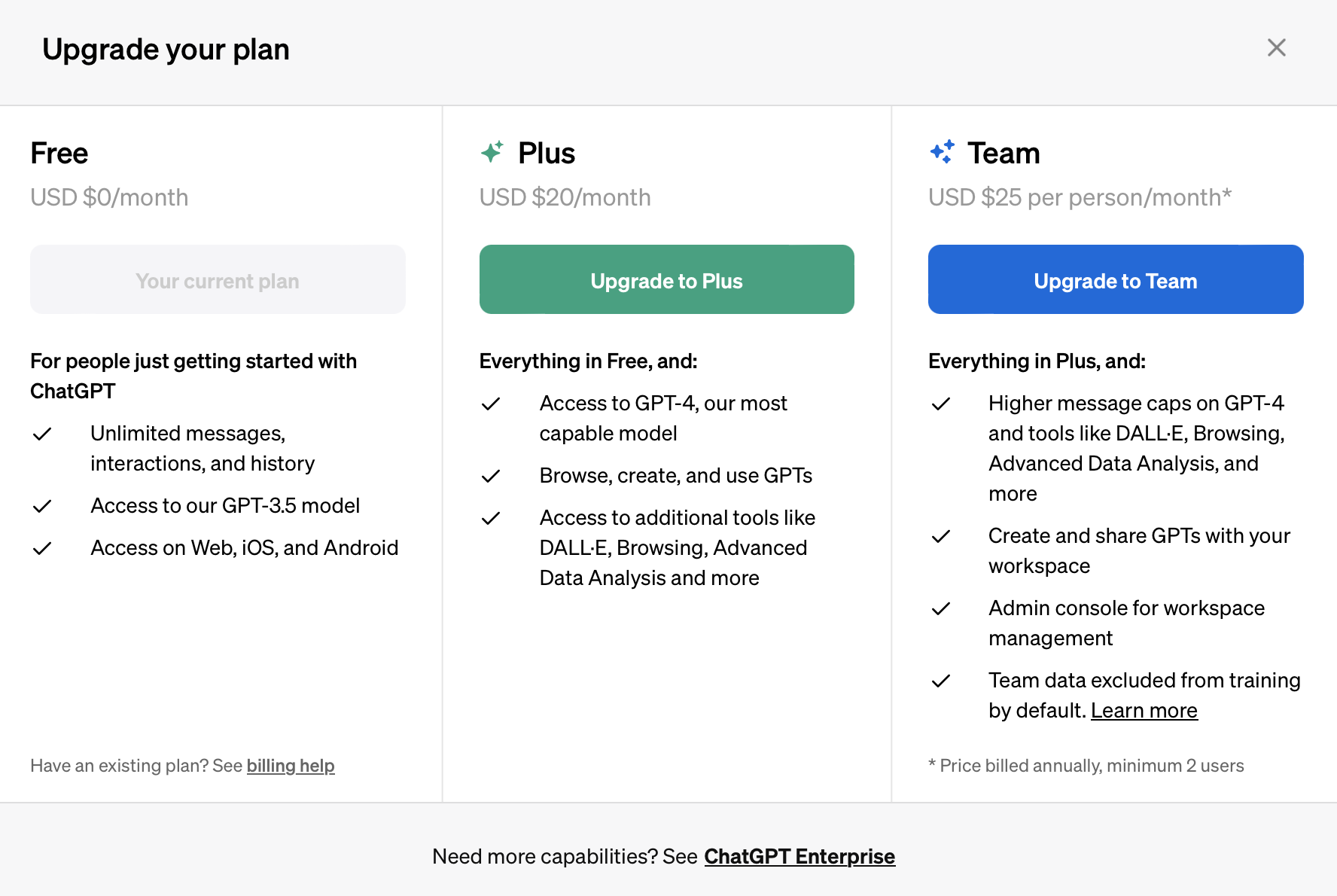
chatgpt plus价格
翻译为中文:

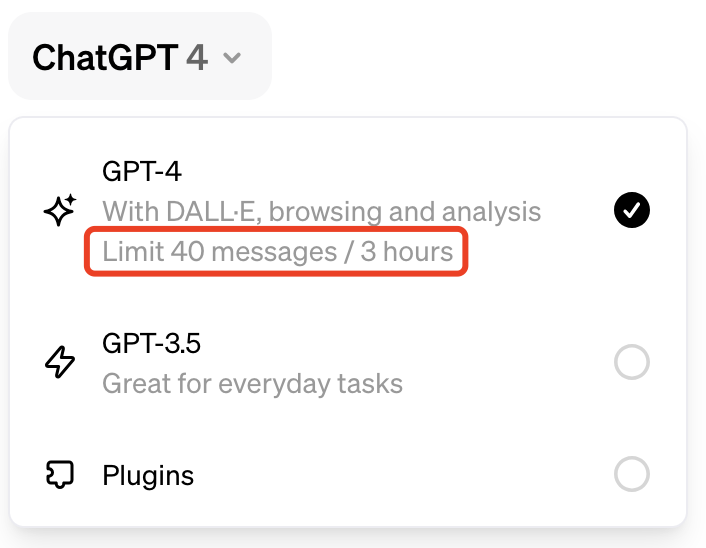
chatgpt plus使用数量限制
逻辑测试一
文心一言4.0的回答:
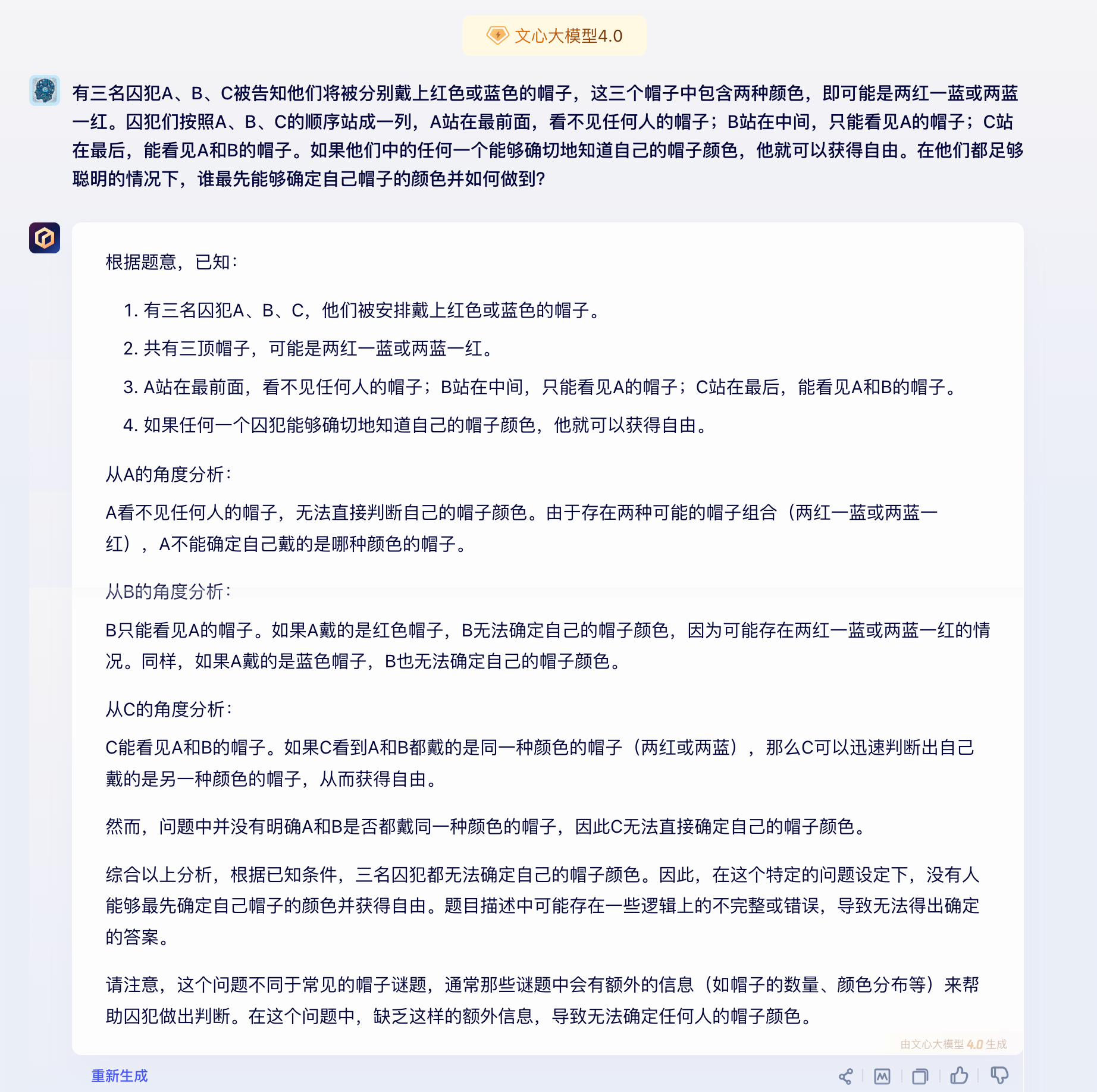
根据题意,已知:
-
有三名囚犯a、b、c,他们被安排戴上红色或蓝色的帽子。
-
共有三顶帽子,可能是两红一蓝或两蓝一红。
-
a站在最前面,看不见任何人的帽子;b站在中间,只能看见a的帽子;c站在最后,能看见a和b的帽子。
-
如果任何一个囚犯能够确切地知道自己的帽子颜色,他就可以获得自由。
从a的角度分析: a看不见任何人的帽子,无法直接判断自己的帽子颜色。由于存在两种可能的帽子组合(两红一蓝或两蓝一红),a不能确定自己戴的是哪种颜色的帽子。
从b的角度分析: b只能看见a的帽子。如果a戴的是红色帽子,b无法确定自己的帽子颜色,因为可能存在两红一蓝或两蓝一红的情况。同样,如果a戴的是蓝色帽子,b也无法确定自己的帽子颜色。
从c的角度分析: c能看见a和b的帽子。如果c看到a和b都戴的是同一种颜色的帽子(两红或两蓝),那么c可以迅速判断出自己戴的是另一种颜色的帽子,从而获得自由。
然而,问题中并没有明确a和b是否都戴同一种颜色的帽子,因此c无法直接确定自己的帽子颜色。
综合以上分析,根据已知条件,三名囚犯都无法确定自己的帽子颜色。因此,在这个特定的问题设定下,没有人能够最先确定自己帽子的颜色并获得自由。题目描述中可能存在一些逻辑上的不完整或错误,导致无法得出确定的答案。
请注意,这个问题不同于常见的帽子谜题,通常那些谜题中会有额外的信息(如帽子的数量、颜色分布等)来帮助囚犯做出判断。在这个问题中,缺乏这样的额外信息,导致无法确定任何人的帽子颜色。
文心一言3.5的回答:
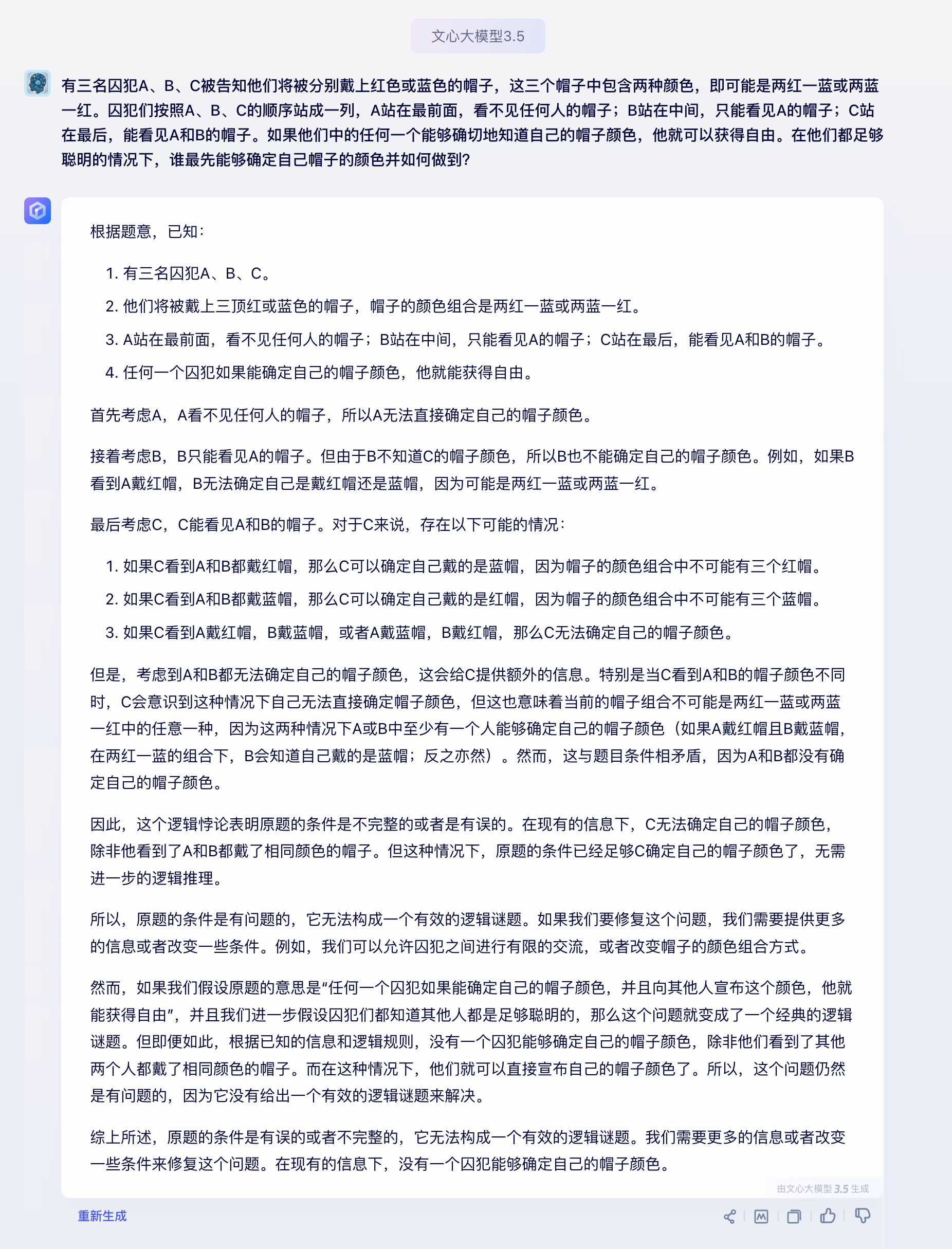
根据题意,已知:
-
有三名囚犯a、b、c。
-
他们将被戴上三顶红或蓝色的帽子,帽子的颜色组合是两红一蓝或两蓝一红。
-
a站在最前面,看不见任何人的帽子;b站在中间,只能看见a的帽子;c站在最后,能看见a和b的帽子。
-
任何一个囚犯如果能确定自己的帽子颜色,他就能获得自由。
首先考虑a,a看不见任何人的帽子,所以a无法直接确定自己的帽子颜色。
接着考虑b,b只能看见a的帽子。但由于b不知道c的帽子颜色,所以b也不能确定自己的帽子颜色。例如,如果b看到a戴红帽,b无法确定自己是戴红帽还是蓝帽,因为可能是两红一蓝或两蓝一红。
最后考虑c,c能看见a和b的帽子。对于c来说,存在以下可能的情况:
-
如果c看到a和b都戴红帽,那么c可以确定自己戴的是蓝帽,因为帽子的颜色组合中不可能有三个红帽。
-
如果c看到a和b都戴蓝帽,那么c可以确定自己戴的是红帽,因为帽子的颜色组合中不可能有三个蓝帽。
-
如果c看到a戴红帽,b戴蓝帽,或者a戴蓝帽,b戴红帽,那么c无法确定自己的帽子颜色。
但是,考虑到a和b都无法确定自己的帽子颜色,这会给c提供额外的信息。特别是当c看到a和b的帽子颜色不同时,c会意识到这种情况下自己无法直接确定帽子颜色,但这也意味着当前的帽子组合不可能是两红一蓝或两蓝一红中的任意一种,因为这两种情况下a或b中至少有一个人能够确定自己的帽子颜色(如果a戴红帽且b戴蓝帽,在两红一蓝的组合下,b会知道自己戴的是蓝帽;反之亦然)。然而,这与题目条件相矛盾,因为a和b都没有确定自己的帽子颜色。
因此,这个逻辑悖论表明原题的条件是不完整的或者是有误的。在现有的信息下,c无法确定自己的帽子颜色,除非他看到了a和b都戴了相同颜色的帽子。但这种情况下,原题的条件已经足够c确定自己的帽子颜色了,无需进一步的逻辑推理。
所以,原题的条件是有问题的,它无法构成一个有效的逻辑谜题。如果我们要修复这个问题,我们需要提供更多的信息或者改变一些条件。例如,我们可以允许囚犯之间进行有限的交流,或者改变帽子的颜色组合方式。
然而,如果我们假设原题的意思是“任何一个囚犯如果能确定自己的帽子颜色,并且向其他人宣布这个颜色,他就能获得自由”,并且我们进一步假设囚犯们都知道其他人都是足够聪明的,那么这个问题就变成了一个经典的逻辑谜题。但即便如此,根据已知的信息和逻辑规则,没有一个囚犯能够确定自己的帽子颜色,除非他们看到了其他两个人都戴了相同颜色的帽子。而在这种情况下,他们就可以直接宣布自己的帽子颜色了。所以,这个问题仍然是有问题的,因为它没有给出一个有效的逻辑谜题来解决。
综上所述,原题的条件是有误的或者不完整的,它无法构成一个有效的逻辑谜题。我们需要更多的信息或者改变一些条件来修复这个问题。在现有的信息下,没有一个囚犯能够确定自己的帽子颜色。
chatgpt4.0的回答:
在这个问题中,我们可以通过逻辑推理来确定谁能最先确切地知道自己的帽子颜色。
首先,c站在最后,能看见a和b的帽子。如果a和b的帽子颜色相同,那么c就能立即知道自己的帽子是另一种颜色,因为只有两种颜色的帽子,且帽子的总组合是两顶一色和一顶另一色。例如,如果a和b都戴红帽,c就知道自己必须戴蓝帽,反之亦然。然而,如果c没有立即回答,那意味着a和b的帽子颜色不同,因为c无法确定自己的帽子颜色。
接下来,b站在中间,只能看到a的帽子。如果c没有立即回答(表示a和b帽子颜色不同),b就可以推理出自己的帽子颜色。因为如果a的帽子颜色是b能看到的唯一颜色,那么b知道自己的帽子必须是另一种颜色以满足“两顶一色,一顶另一色”的规则。例如,如果b看到a戴的是红帽,而c没有立即回答(表明b和a的帽子颜色不同),那么b可以确定自己的帽子是蓝色的。
因此,如果c看到a和b戴的帽子颜色相同,c可以立即知道自己的帽子颜色并获得自由。如果c不能确定自己的帽子颜色(意味着a和b帽子颜色不同),则b通过排除法可以确定自己的帽子颜色。a没有足够的信息来确定自己的帽子颜色,因为a看不见任何人的帽子。
总结来说,c如果看到a和b戴相同颜色的帽子,他将是第一个能够确定自己帽子颜色的人。如果c不能确定,那么b将是第一个通过逻辑推理确定自己帽子颜色的人。

chatgpt3.5的回答:
囚犯c最先能够确定自己帽子的颜色。
让我们分析一下:
-
a 看不见任何人的帽子,因此他无法提供任何有用的信息。
-
b 只能看见 a 的帽子。如果 a 和 b 的帽子颜色相同,那么 c 的帽子颜色就是相反的,因为三个帽子中包含两种颜色。但如果 a 和 b 的帽子颜色不同,那么 b 就无法确定自己的帽子颜色,因为有两种可能性。所以 b 无法提供关于 c 帽子颜色的确定信息。
-
c 能够看见 a 和 b 的帽子。如果 a 和 b 的帽子颜色相同,那么 c 的帽子颜色就是相反的。如果 a 和 b 的帽子颜色不同,那么 c 就能够确定自己的帽子颜色,因为在三个帽子中必须有两种颜色,所以 c 能够确定自己的帽子颜色。
因此,囚犯c最先能够确定自己帽子的颜色。

结论
chatgpt4.0 > chatgpt3.5 > 文心一言4.0 = 文心一言3.5
首先,只有chatgpt4.0回答出了完整的逻辑链,正确地说出了“如果c没有立即回答(表示a和b帽子颜色不同),b就可以推理出自己的帽子颜色”这一推论。chatgpt3.5缺少了最后这条推论。而文心一言4.0和文心一言3.5也正确地说出了比较浅显的几条结论,但他们最后给出的结论是“题目缺少条件”,这是赤裸裸的“ai幻觉”。
逻辑测试二
文心一言4.0的回答:
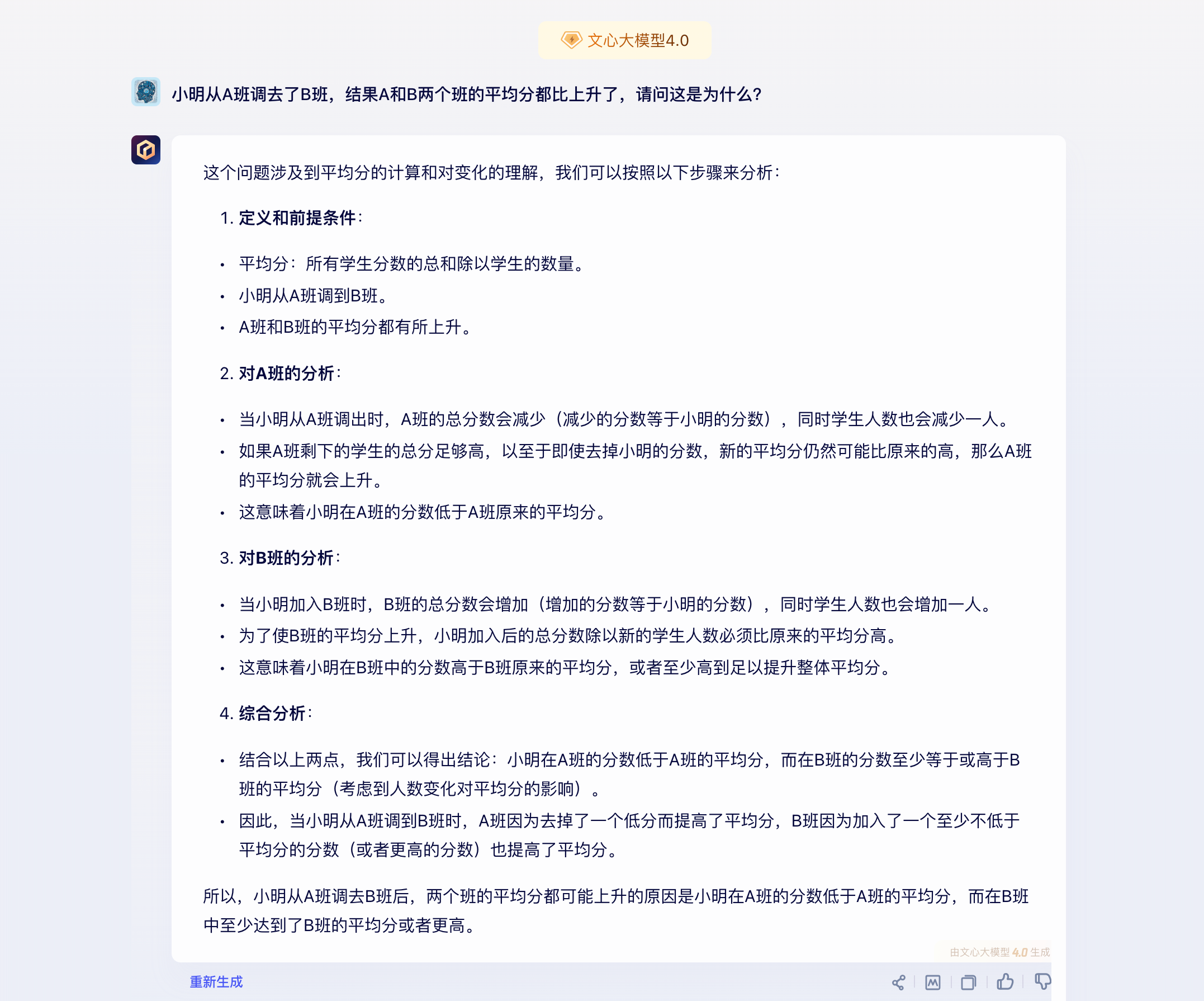
这个问题涉及到平均分的计算和对变化的理解,我们可以按照以下步骤来分析:
-
定义和前提条件:
-
平均分:所有学生分数的总和除以学生的数量。
-
小明从a班调到b班。
-
a班和b班的平均分都有所上升。
-
对a班的分析:
-
当小明从a班调出时,a班的总分数会减少(减少的分数等于小明的分数),同时学生人数也会减少一人。
-
如果a班剩下的学生的总分足够高,以至于即使去掉小明的分数,新的平均分仍然可能比原来的高,那么a班的平均分就会上升。
-
这意味着小明在a班的分数低于a班原来的平均分。
-
对b班的分析:
-
当小明加入b班时,b班的总分数会增加(增加的分数等于小明的分数),同时学生人数也会增加一人。
-
为了使b班的平均分上升,小明加入后的总分数除以新的学生人数必须比原来的平均分高。
-
这意味着小明在b班中的分数高于b班原来的平均分,或者至少高到足以提升整体平均分。
-
综合分析:
-
结合以上两点,我们可以得出结论:小明在a班的分数低于a班的平均分,而在b班的分数至少等于或高于b班的平均分(考虑到人数变化对平均分的影响)。
-
因此,当小明从a班调到b班时,a班因为去掉了一个低分而提高了平均分,b班因为加入了一个至少不低于平均分的分数(或者更高的分数)也提高了平均分。
所以,小明从a班调去b班后,两个班的平均分都可能上升的原因是小明在a班的分数低于a班的平均分,而在b班中至少达到了b班的平均分或者更高。
文心一言3.5的回答:
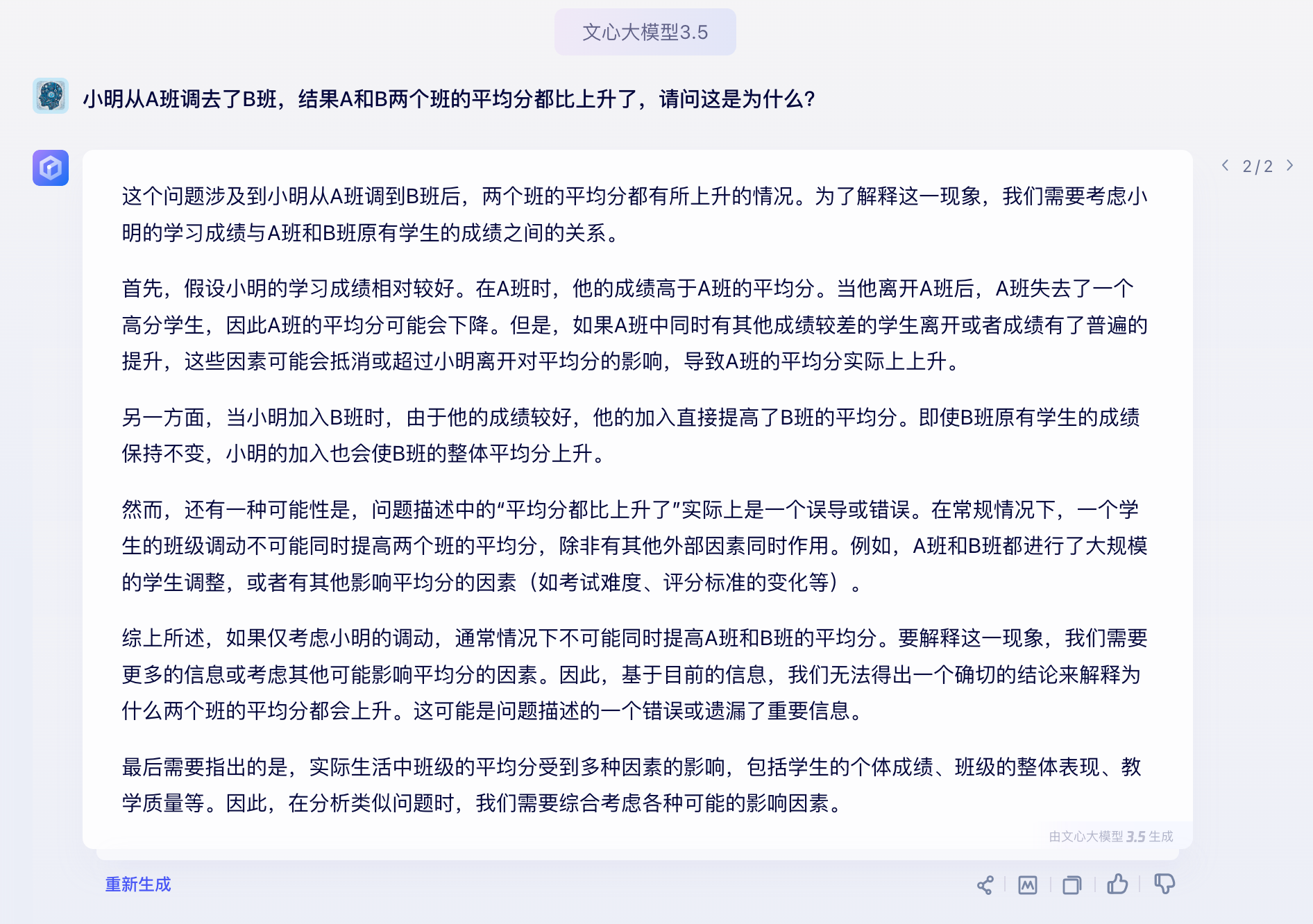
这个问题涉及到小明从a班调到b班后,两个班的平均分都有所上升的情况。为了解释这一现象,我们需要考虑小明的学习成绩与a班和b班原有学生的成绩之间的关系。
首先,假设小明的学习成绩相对较好。在a班时,他的成绩高于a班的平均分。当他离开a班后,a班失去了一个高分学生,因此a班的平均分可能会下降。但是,如果a班中同时有其他成绩较差的学生离开或者成绩有了普遍的提升,这些因素可能会抵消或超过小明离开对平均分的影响,导致a班的平均分实际上上升。
另一方面,当小明加入b班时,由于他的成绩较好,他的加入直接提高了b班的平均分。即使b班原有学生的成绩保持不变,小明的加入也会使b班的整体平均分上升。
然而,还有一种可能性是,问题描述中的“平均分都比上升了”实际上是一个误导或错误。在常规情况下,一个学生的班级调动不可能同时提高两个班的平均分,除非有其他外部因素同时作用。例如,a班和b班都进行了大规模的学生调整,或者有其他影响平均分的因素(如考试难度、评分标准的变化等)。
综上所述,如果仅考虑小明的调动,通常情况下不可能同时提高a班和b班的平均分。要解释这一现象,我们需要更多的信息或考虑其他可能影响平均分的因素。因此,基于目前的信息,我们无法得出一个确切的结论来解释为什么两个班的平均分都会上升。这可能是问题描述的一个错误或遗漏了重要信息。
最后需要指出的是,实际生活中班级的平均分受到多种因素的影响,包括学生的个体成绩、班级的整体表现、教学质量等。因此,在分析类似问题时,我们需要综合考虑各种可能的影响因素。
chatgpt4.0的回答:
这个问题是经典的统计学悖论之一,称为“辛普森悖论”(simpson's paradox)。这种悖论说明,在分组数据中观察到的趋势可能会与将这些数据合并后观察到的趋势完全相反。具体到小明从a班调到b班这个问题,导致两个班的平均分都提高的原因可能是小明的分数处于两个班级平均分之间,使得他调班后既提高了a班的平均分(因为去除了一个低于a班平均分的学生),也提高了b班的平均分(因为加入了一个高于b班平均分的学生)。下面是一个简化的例子来解释这个现象:
假设:
-
a班有10个学生,平均分为70分。
-
b班有10个学生,平均分为60分。
-
小明的分数是65分。
当小明从a班调到b班时:
-
a班的总分减少了小明的65分,但平均分计算时的分母也相应减少了1,这可能导致a班剩余学生的平均分略有提高。
-
b班的总分增加了小明的65分,平均分计算时的分母增加了1,由于小明的分数高于b班原有的平均分,这会提高b班的平均分。
这个悖论的关键在于分组和整体平均的差异。调动个别数据点(在这个例子中是小明的分数)可能对分组平均产生重大影响,尤其是当这些数据点与分组的平均值相比有显著差异时。因此,即使小明的加入或退出只对两个班级的总分和人数产生微小变化,也足以改变平均分的计算结果,从而导致辛普森悖论现象。

chatgpt3.5的回答:
这种情况可能是由于小明的平均分高于b班的平均分,但低于a班的平均分,导致他离开a班后,a班的平均分上升,而他加入b班后,b班的平均分也上升了。
假设小明在a班的平均分为x,a班的总分为a,学生人数为a;小明在b班的平均分为y,b班的总分为b,学生人数为b。
那么,小明离开a班后,a班的平均分变为(a - x) / (a - 1),小明加入b班后,b班的平均分变为(b + y) / (b + 1)。
由于题目中提到a和b两个班的平均分都比上升了,即:
(a - x) / (a - 1) > x,并且 (b + y) / (b + 1) > y
解这两个不等式可得:
a > x * (a - 1) + x,以及 b < y * (b + 1) - y
如果小明的分数足够高,使得上述不等式成立,那么小明从a班调去b班后,a和b两个班的平均分都会上升。

结论
chatgpt4.0 > 文心一言4.0 >= chatgpt3.5 > 文心一言3.5
chatgpt4.0在深度和广度上领先,因为它不仅解释了问题,还引入了辛普森悖论这一更广泛的统计学概念来加深理解。文心一言4.0在逻辑性和准确性方面表现也很不错,但我个人感觉没有chatgpt4.0解释地清晰明了和深入。chatgpt3.5同样准确地识别了问题的核心,即小明的分数在a班和b班平均分之间的位置。
精选推荐
都读到这里了,点个赞鼓励一下吧😊👍👍👍。关注我,ai之路不迷路,原创技术文章第一时间推送🤖。



发表评论