相关文章:
前言
本文是对于《手搓神经网络——bp反向传播》一文中高级的 bp 反向传播部分的详细论述
import numpy as np
import tensorflow as tf
输入,权重与偏置
输入,权重与偏置的属性
先来聊聊输入(x)、权重(w)、偏置(b)。无需再废话的是,这三者的类型都是数组numpy.ndarray
输入(x)
输入(x)的形状为(b, n),b表示 batch_size(批大小),n表示输入询量数据长度。下图表示 batch_size 为b的每个训练数据形状为(1, n)的训练集

输入矩阵中,x 上标表示此训练数据在一个批大小中的位置,x 下标表示第b个训练数据的第n个参数
权重(w)
权重(w)的形状为(n, m),n表示输入数据数量,m表示该层输出数据数量(即该层的神经元数量)
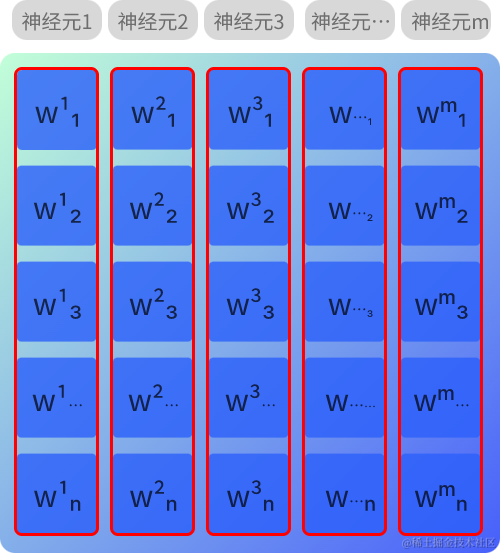
在全连接层中,每层的各个神经元相互交织连接。权重矩阵中,w 上标表示的是该层的第 m 个神经元,w 下标表示的是该层第 m 个神经元与第 n 个输入的联系
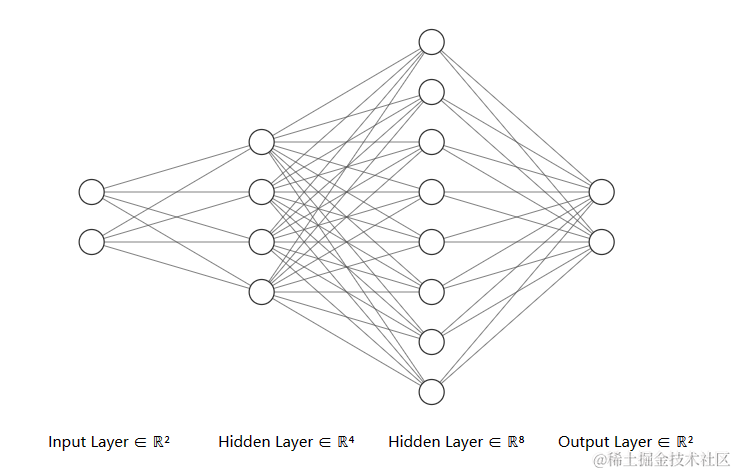
偏置(b)
偏置(b)的形状为(1, m),m表示该层输出数据数量(即该层的神经元数量),图中的 b1、b2、b3…分别表示神经元1、神经元2、神经元3…的偏置

输入,权重与偏置的计算
关于计算不多赘述,就是
x
@
w
+
b
x@w+b
x@w+b ,在本文中@表示矩阵叉乘,用numpy表示即为x@w+b或者np.dot(x, w)+b,在将其计算结果带入激活函数,得到的即为神经网络层的输出,笔者认为前向运算的本质就是矩阵计算,反向传播的本质就是矩阵求导
矩阵求导
在输出层计算部分之前,单独论述下矩阵求导。主要论述x@w+b 对 w 求导与激活函数对 x@w+b 的求导
x@w+b 对 w 求导
下面有一个x@w+b表达式,嚯!看着挺复杂的,实则是笔者这里写的详细了些,与其说复杂倒不如是繁琐
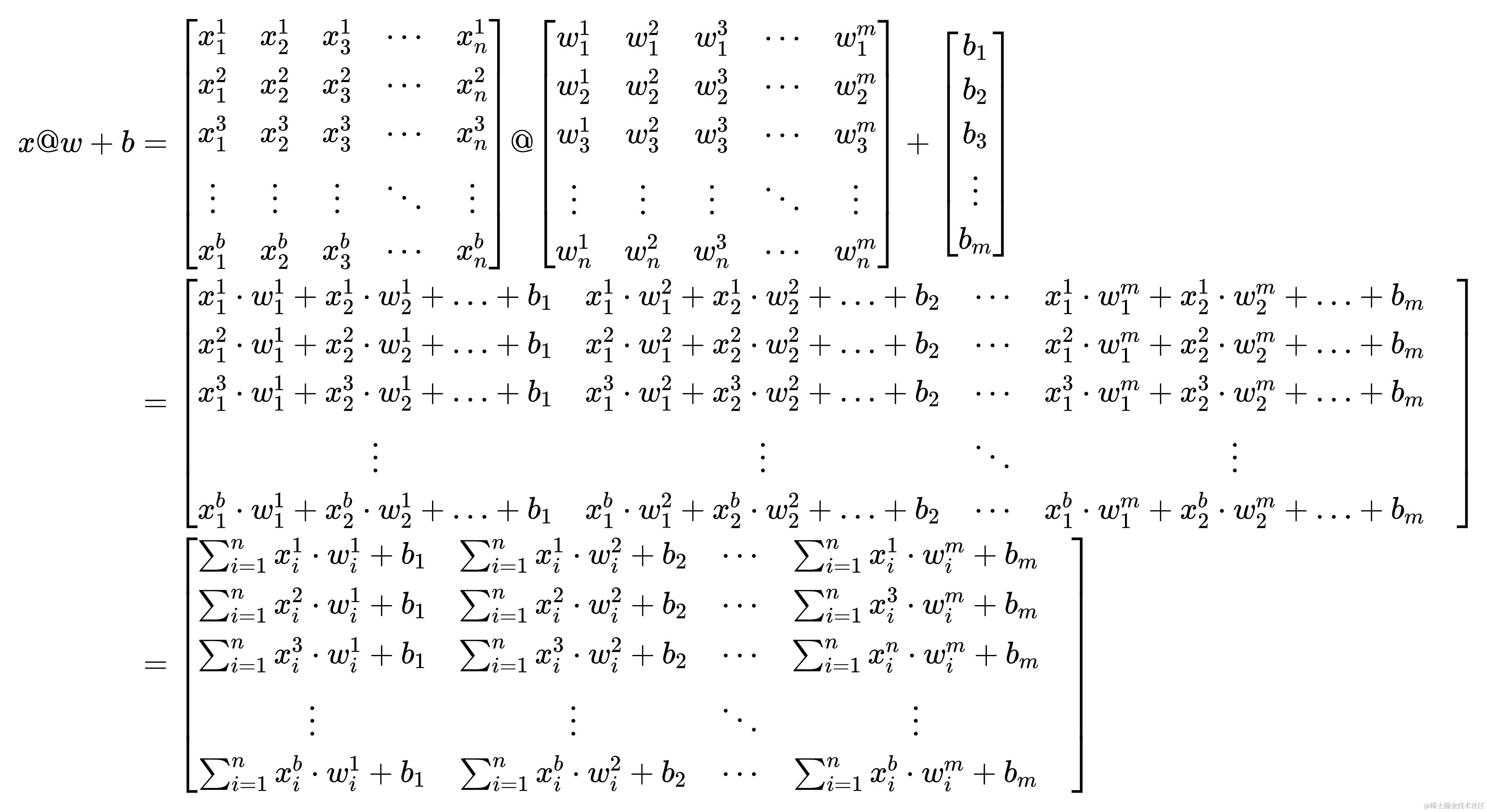
接下来,加一点魔法🪄,让x@w+b叉乘✖一个形状为(m, 1)的全一矩阵(矩阵里全是一①ⅰ壹),m与权重(w)中m的含义相同。将这个矩阵记作
α
1
\alpha_{1}
α1。哈哈,好像高中写数学题,要化简时经常要用到神奇的1
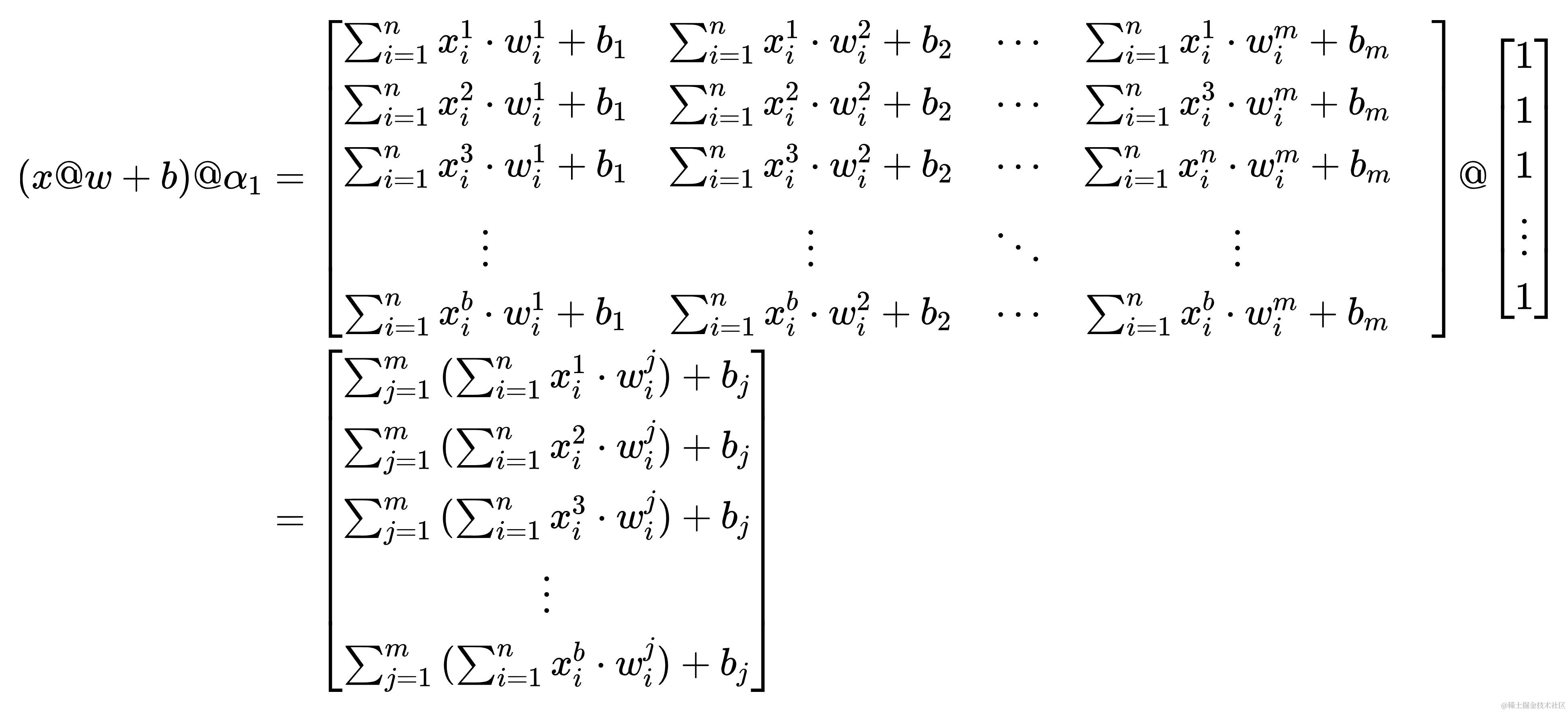
这样子,得出的结果看着就简洁多了。然后如法炮制,只不过是让一个形状为(1, b)的全一矩阵叉乘✖
(
x
@
w
+
b
)
@
α
1
(x@w+b)@\alpha_{1}
(x@w+b)@α1,将这个矩阵记作
α
2
\alpha_{2}
α2。哈哈哈,汗流浃背了吧,兄弟😅,你八成是看傻了,我两成是写傻了

经过一坨又一坨的变换,最终以一个标量的表达式来表示最初的x@w+b(
α
1
\alpha_{1}
α1 与
α
2
\alpha_{2}
α2 是为了化简成上方的形式而存在的,之所以要化简成上方形式是为了使表达式更简洁,也是为了便于对w求导)
计算 ∑ k = 1 b ∑ j = 1 m ∑ i = 1 n x i k ⋅ w i j + b j \sum_{k=1}^{b}{\sum_{j=1}^{m}{\sum_{i=1}^{n}{x_{i}^{k} \cdot w_{i}^{j}} + b_{j}}} ∑k=1b∑j=1m∑i=1nxik⋅wij+bj 对 w i j w_{i}^{j} wij 的导数
d y d w i j = d d w i j ∑ k = 1 b ∑ j = 1 m ∑ i = 1 n x i k ⋅ w i j + b j = ∑ k = 1 b x i k \frac{\mathrm{dy}}{\mathrm{d}w_{i}^{j}} = \frac{\mathrm{d}}{\mathrm{d}w_{i}^{j}} \sum_{k=1}^{b}{\sum_{j=1}^{m}{\sum_{i=1}^{n}{x_{i}^{k} \cdot w_{i}^{j}} + b_{j}}} = \sum_{k=1}^{b}{x_{i}^{k}} dwijdy=dwijdk=1∑bj=1∑mi=1∑nxik⋅wij+bj=k=1∑bxik
自此长篇大论得出的结论,x@w+b对w的导数表示成矩阵形式为
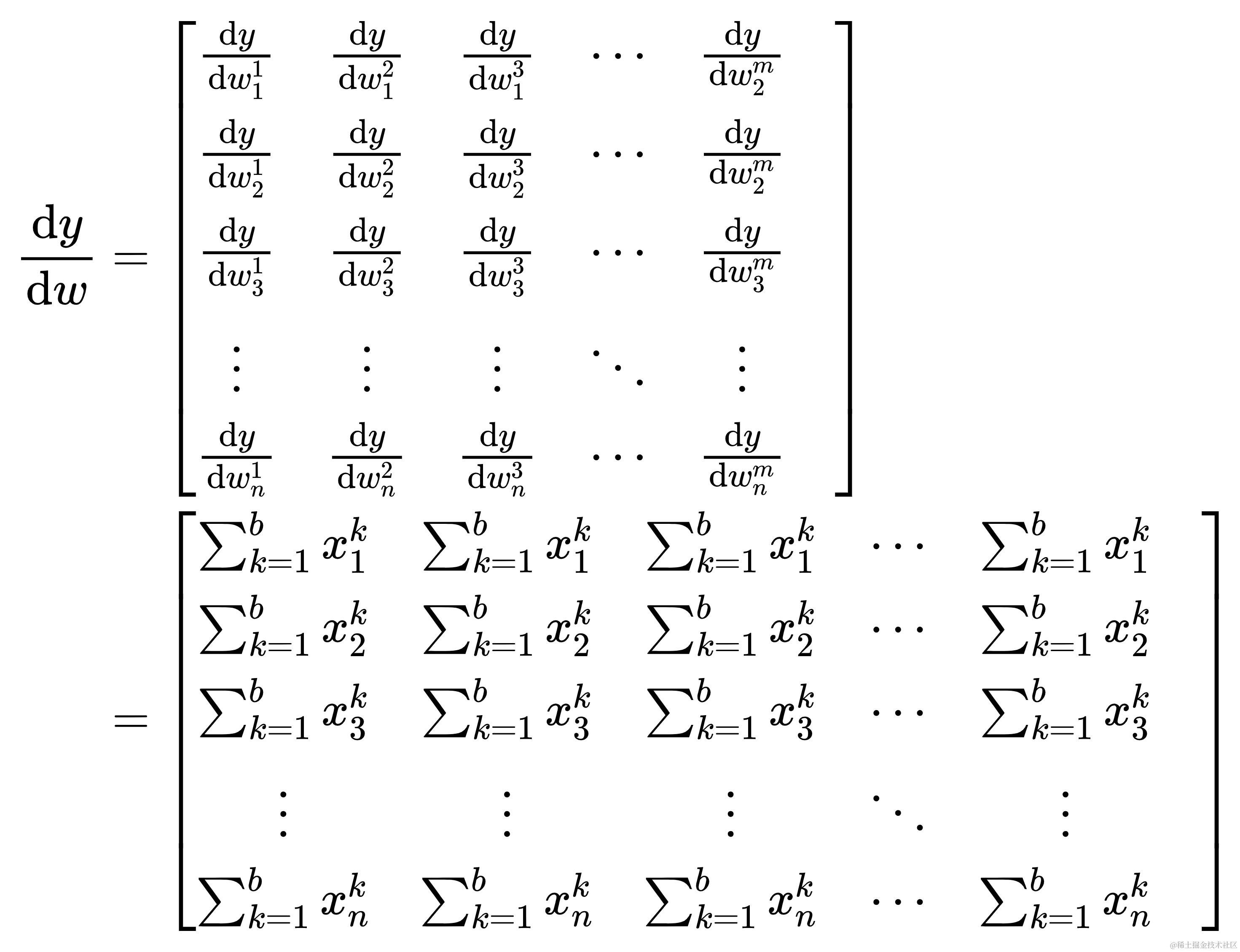
可以看得出x@w+b 对 w 的导数为 x 矩阵转置的行之和,且重复扩展成原形状(不是哥,你要问我怎么看出来是转置的?熟读并抄写10遍上文,还不晓得?熟读全文并背诵)
上面的话似乎有些难以理解,来点魔法。将形状为(b, m)全一矩阵记作
α
3
\alpha_{3}
α3,用数学的语言表达如下
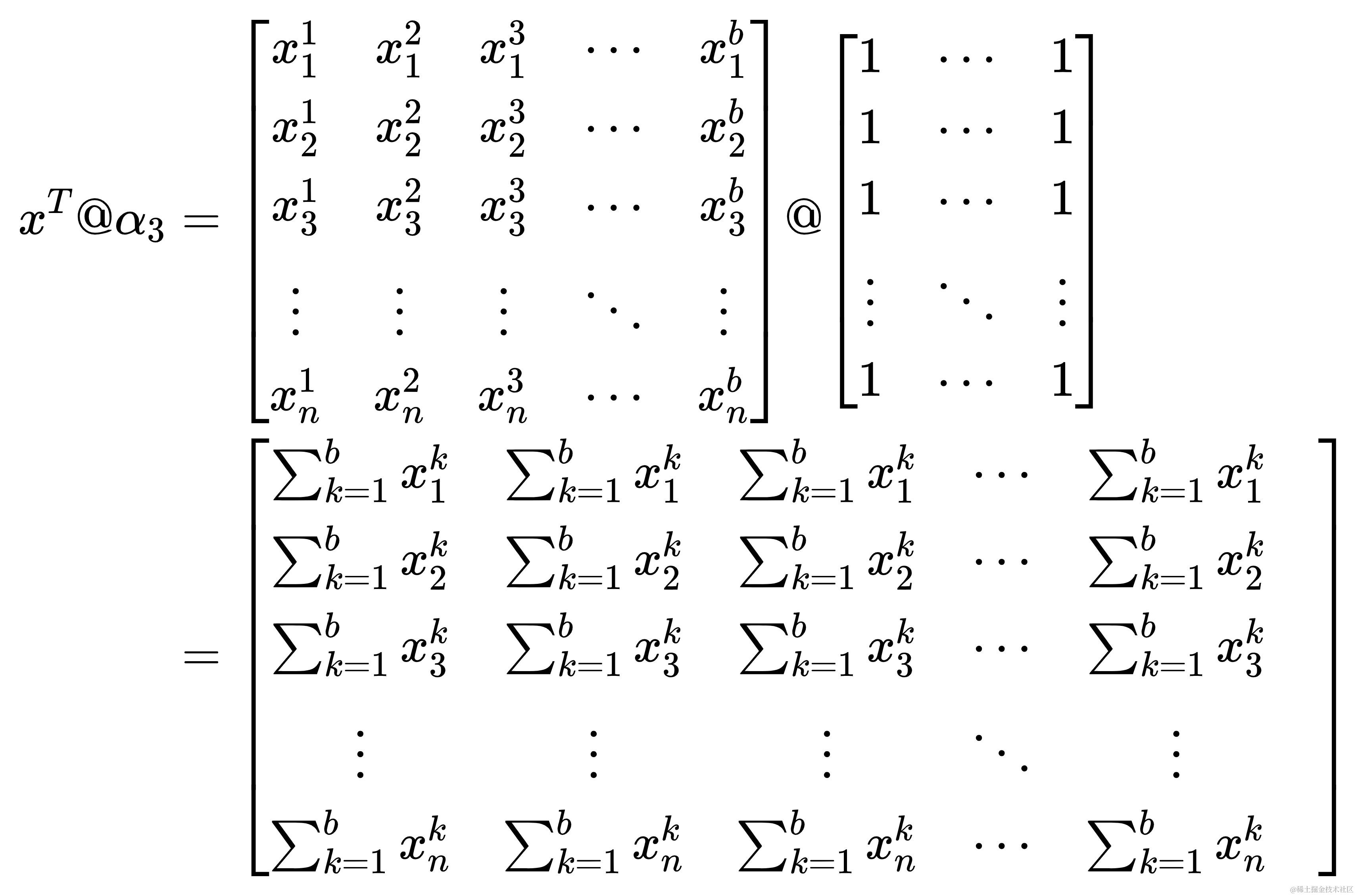
α 3 \alpha_{3} α3 的应用实现了两个功能,即上文所述的求行之和与重复扩展
- 求行之和:在矩阵叉乘中,可视为
x
t
x^{t}
xt 的行与
α
3
\alpha_{3}
α3 的列的点乘求和
- 具体来说, x t @ α 3 x^{t}@\alpha_{3} xt@α3 的结果是一个列向量,其第 i 个元素是 x t x^{t} xt 的每一行的元素与 α 3 \alpha_{3} α3 的第 i 列的元素相乘并求和的结果。由于 α 3 \alpha_{3} α3 的每一列全是1,这意味着每一行的所有元素都会被加起来。因此, x t @ α 3 x^{t}@α3 xt@α3 的结果实际上是 x t x^{t} xt 的每一行的元素之和
- 重复扩展:在矩阵叉乘中,可视为
x
t
x^{t}
xt 的行与
α
3
\alpha_{3}
α3 的列运算
- 由于
x
t
x^{t}
xt 的形状是
(n, b), α 3 \alpha_{3} α3 的形状是(b, m),这意味着在两个矩阵运算后,得到的的结果为一个形状为(n, m)的矩阵,这与 w w w 的形状一致
- 由于
x
t
x^{t}
xt 的形状是
最后一句话收尾:
d x @ w + b d w = x t @ α , α 形状为 ( b , m ) \frac{\mathrm{d}\ x@w+b}{\mathrm{d} w} = x^{t} @ \alpha\ ,\alpha形状为(b, m) dwd x@w+b=xt@α ,α形状为(b,m)
激活函数对 w 的求导
根据链式法则,将激活函数(以sigmoid为例)对 w 进行求导。但在这里可以用
s
i
g
m
o
i
d
′
sigmoid\ '
sigmoid ′ 代替
α
3
\alpha_{3}
α3,因为
s
i
g
m
o
i
d
sigmoid
sigmoid 的形状与
α
3
\alpha_{3}
α3 一致,所以所起的功能也一样
x
→
x
@
w
+
b
→
s
i
g
m
o
i
d
(
x
@
w
+
b
)
x
t
@
s
i
g
m
o
i
d
′
\begin{align*} x →\ &x@w+b &&→ &&sigmoid(x@w+b) \\ &x^{t} &&@ &&sigmoid\ ' \end{align*}
x→ x@w+bxt→@sigmoid(x@w+b)sigmoid ′
可得结论:
d
a
c
t
i
v
a
t
i
o
n
(
x
@
w
+
b
)
d
w
=
x
t
@
a
c
t
i
v
a
t
i
o
n
′
\frac{\mathrm{d}\ activation(x@w+b)}{\mathrm{d} w} = x^{t} @ activation\ '
dwd activation(x@w+b)=xt@activation ′
x@w+b 对 x 求导
loss对w、b求导是为了更新权重(w)、偏置(b),可why这里还要来对x求导。都说bp反向传播,哎,是吧?对x求导就是为了实现“传播”,具体的到误差传播部分在和你逼逼赖赖
回到正题,这个怎么弄,具体的就不多言了。与上面的方法大差不差,不过是照本宣科罢了。写的一坨一坨的都,是吧?反正也没人看。那就直接下结论了
d x @ w + b d x = α @ w t , α 形状为 ( b , m ) \frac{\mathrm{d}\ x@w+b}{\mathrm{d} x} = \alpha @ w^{t}\ ,\alpha形状为(b, m) dxd x@w+b=α@wt ,α形状为(b,m)
激活函数 对 x 求导
这儿也是,直接结论了
d a c t i v a t i o n ( x @ w + b ) d x = a c t i v a t i o n ′ @ w t \frac{\mathrm{d}\ activation(x@w+b)}{\mathrm{d} x} = activation\ ' @ w^{t} dxd activation(x@w+b)=activation ′@wt
再回首——高级的 bp 反向传播
既然是对《手搓神经网络——bp反向传播》一文中高级的 bp 反向传播部分的详细论述。那就再回到这一部分,来瞅瞅这里边的计算过程
这里构建的是一个极为简单的神经网络
- 输入层:1个神经元
- 隐藏层:3个神经元
- 输出层:1个神经元
模型图如下
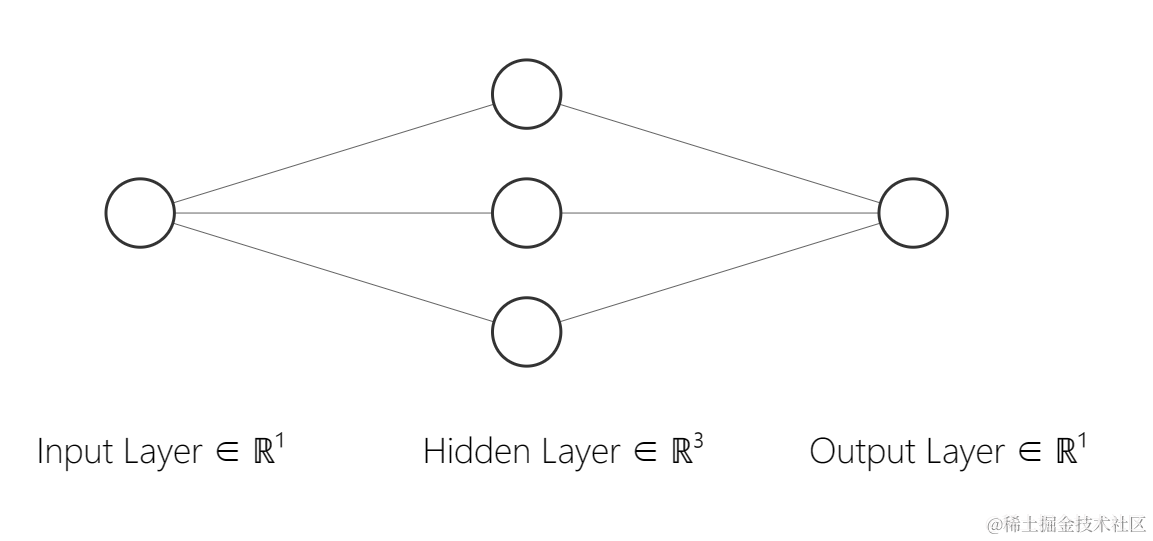
前向计算
👉关于前向计算,这里忽略了激活函数(因为作图时忘了激活函数,不想重作)。但实际上,激活函数还是存在的,在后面的反向求导部分中,仍然会考虑激活函数的计算👈
隐藏层计算
在这里输入(x)的 batch_size 为1,以下分别是隐藏层内的计算过程的可视化图与算式
这里的隐藏层输出的形状实际应为(1, 3),考虑美观这里故画作(3, 1)
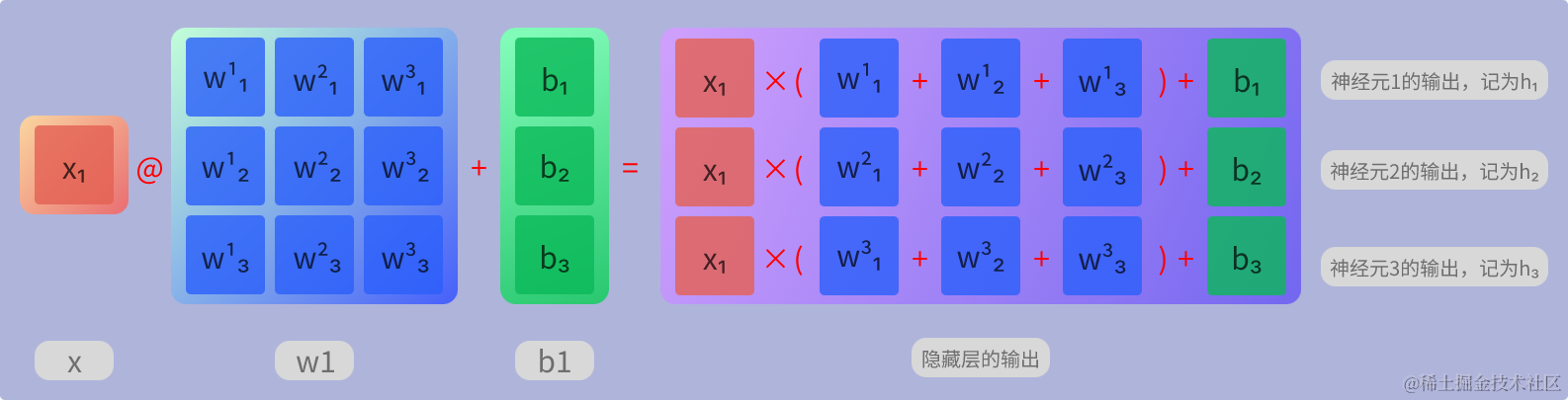
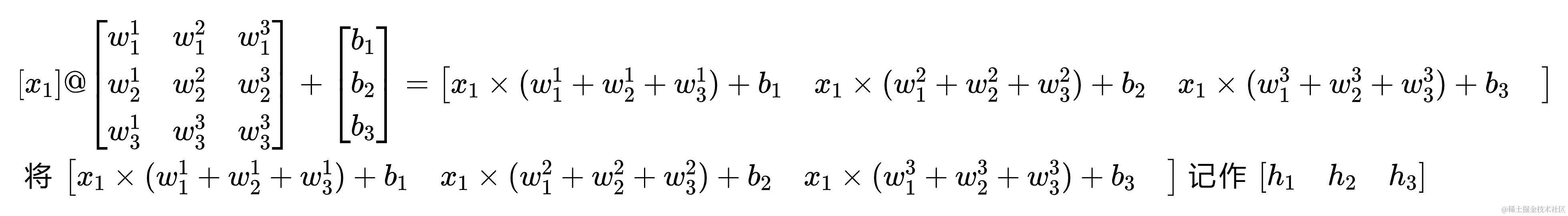
输出层计算
以下分别是输出层内的计算过程的可视化图与算式
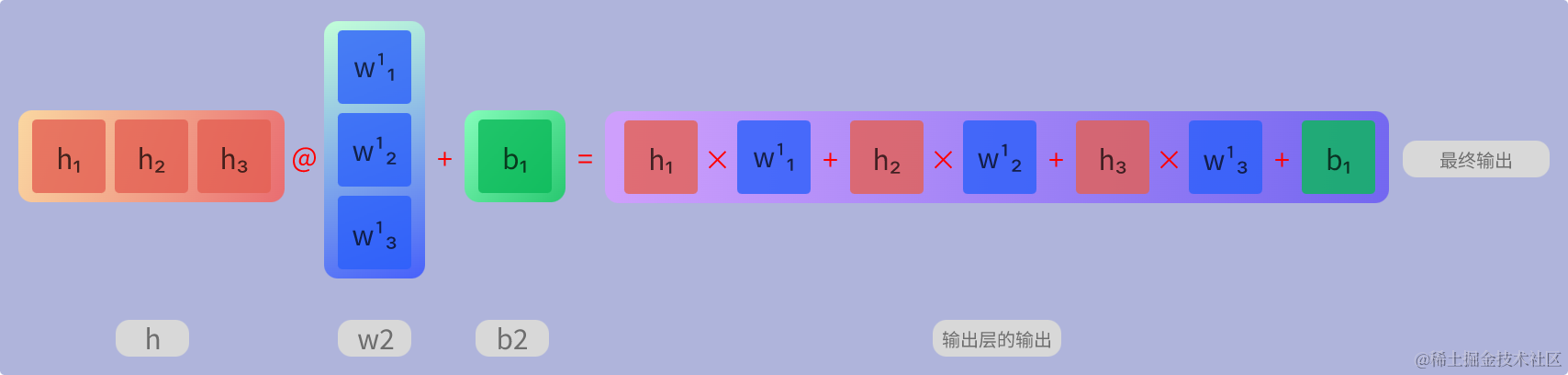
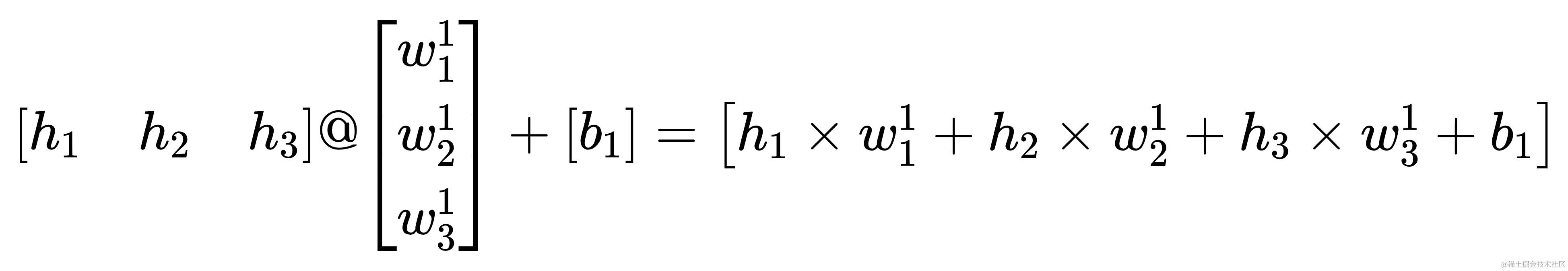
反向求导
关于反向求导,这里说白了就是计算损失loss对其权重(w)、偏置(b)的导数。但在前文矩阵求导中已经细细讲解过,现在是实际应用的时候了
为了简化后面的式子,这里先提前作规定。
h
h
h 与
s
i
g
m
o
i
d
1
sigmoid_{1}
sigmoid1 的含义相同,只是别名罢了,这样是为了使后期式子的表达更简洁
$$
\begin{align*}
h &= sigmoid_{1} \
sigmoid_{1} &= sigmoid(x@w_{1}+b_{1}) \
sigmoid_{2} &= sigmoid(h@w_{2}+b_{2}) \
mse &= mse(true, sigmoid_{2}) \
h\ ’ &= sigmoid_{1}\ ’ \
sigmoid_{1}\ ’ &= sigmoid_{1}\cdot(1-sigmoid_{1}) \
sigmoid_{2}\ ’ &= sigmoid_{2}\cdot(1-sigmoid_{2}) \
mse\ ’ &= \frac{2}{n}\cdot(sigmoid_{2}-true) \
\end{align*}
$$
输出层求导
d l o s s d w 2 \frac{\mathrm{d}\ loss}{\mathrm{d} w_{2}} dw2d loss
至此,上面瞎逼乱讲的扯了这么多,再回到最初,来看看 m s e mse mse 怎么对 w 2 w_{2} w2 求导。先来瞧瞧输出层中的计算过程
上面是输出层中的计算过程,下面是各个计算过程的导数。其实就是运用链式法则啦
h
→
h
@
w
2
+
b
2
→
s
i
g
m
o
i
d
2
→
m
s
e
h
t
@
s
i
g
m
o
i
d
2
′
⋅
m
s
e
′
\begin{align*} h → &h@w_{2}+b_{2} &→& &&sigmoid_{2} &→& &&mse \\ &h^{t} &@& &&sigmoid_{2}\ ' &\cdot& &&mse\ ' \end{align*}
h→h@w2+b2ht→@sigmoid2sigmoid2 ′→⋅msemse ′
将下面的各个求导结果相乘 h t @ s i g m o i d 2 ′ ⋅ m s e ′ h^{t} @ sigmoid_{2}\ ' \cdot mse\ ' ht@sigmoid2 ′⋅mse ′ 就是 m s e mse mse 对 w 2 w_{2} w2 的导数
-
two 个为什么
- 为什么
h
t
h^{t}
ht 与
s
i
g
m
o
i
d
2
′
sigmoid_{2}\ '
sigmoid2 ′ 之间是叉乘
@
@
@?
- 因为 d a c t i v a t i o n ( x @ w + b ) d w = x t @ a c t i v a t i o n ′ \frac{\mathrm{d}\ activation(x@w+b)}{\mathrm{d} w} = x^{t} @ activation\ ' dwd activation(x@w+b)=xt@activation ′ 所以 h t @ s i g m o i d ′ h^{t} @ sigmoid\ ' ht@sigmoid ′
- 为什么
s
i
g
m
o
i
d
2
′
sigmoid_{2}\ '
sigmoid2 ′ 与
m
s
e
′
mse\ '
mse ′ 之间是点乘
⋅
\cdot
⋅?
- 因为在
s
i
g
m
o
i
d
2
′
sigmoid_{2}\ '
sigmoid2 ′ 与
m
s
e
′
mse\ '
mse ′ 的计算过程中,不涉及矩阵的叉乘。通俗点说。就是不涉及
@运算符,所以在用链式法则,可当作标量处理
- 因为在
s
i
g
m
o
i
d
2
′
sigmoid_{2}\ '
sigmoid2 ′ 与
m
s
e
′
mse\ '
mse ′ 的计算过程中,不涉及矩阵的叉乘。通俗点说。就是不涉及
损失 l o s s loss loss 对 w 2 w_{2} w2 求导的数学表达式如下
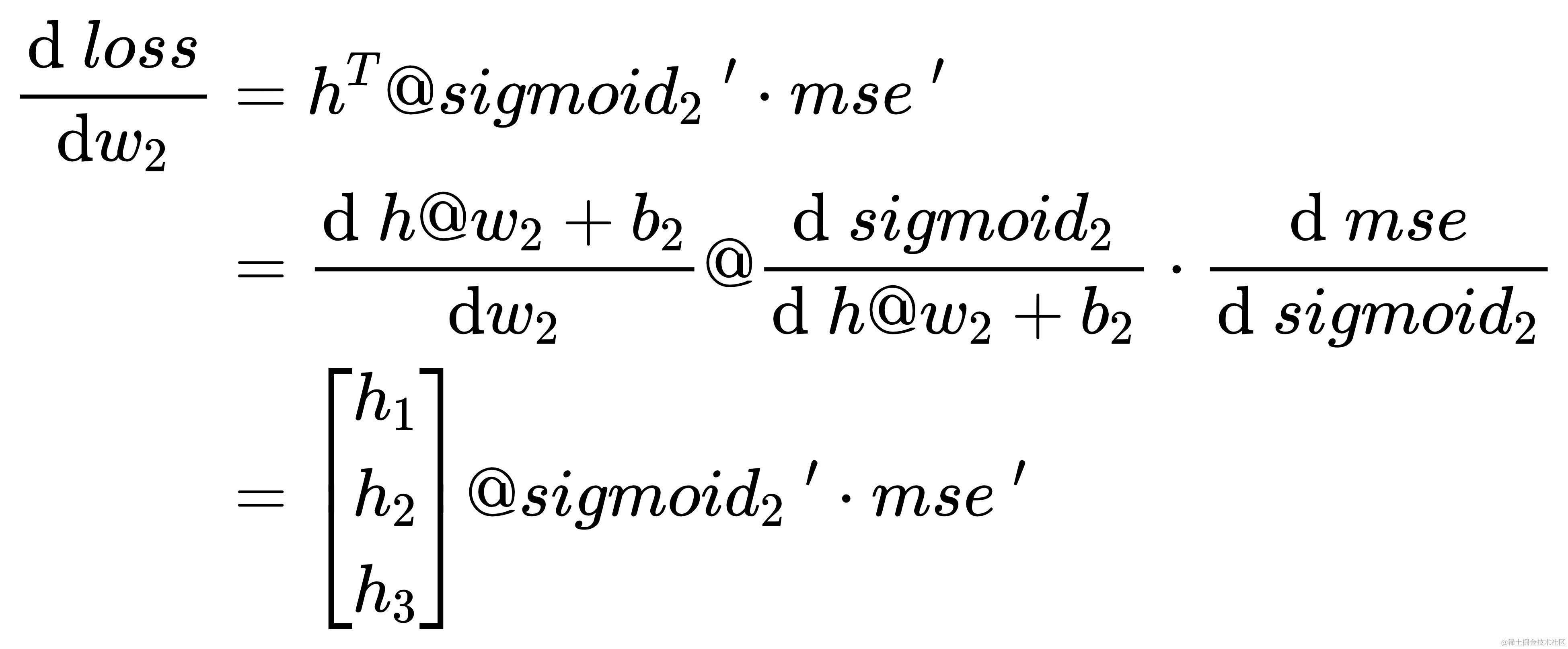
d l o s s d b \frac{\mathrm{d}\ loss}{\mathrm{d} b} dbd loss
哈哈哈,不是吧阿sir,这个还需要再讲吗?嗯哼???😛😛😛只要上面看得懂,这里确实没啥好说的了,就是求导的对象不同而已啦(此对象非彼对象😡💢💢)
根据导数的加法计算法则,有 d l o s s d b 2 = 1 \frac{\mathrm{d}\ loss}{\mathrm{d} b_{2}} = 1 db2d loss=1,所以 l o s s loss loss 对 b 2 b_{2} b2 的导数为1
更新参数
回到《手搓神经网络——bp反向传播》的结论
得到
w
2
w_{2}
w2 的更新计算方式
w
2
n
e
w
−
=
l
r
⋅
h
t
@
s
i
g
m
o
i
d
2
′
⋅
m
s
e
′
w_{2}^{new} -= lr \cdot h^{t}\ @\ sigmoid_{2}\ ' \cdot mse\ '
w2new−=lr⋅ht @ sigmoid2 ′⋅mse ′
得到
b
2
b_{2}
b2 的更新计算方式
b
2
n
e
w
−
=
l
r
⋅
s
i
g
m
o
i
d
2
′
⋅
m
s
e
′
b_{2}^{new} -= lr \cdot sigmoid_{2}\ ' \cdot mse\ '
b2new−=lr⋅sigmoid2 ′⋅mse ′
在《手搓神经网络——bp反向传播》- 高级的 bp 反向传播中,故
w2更新方式:w2 -= lr * h.t @ sigmoid.diff(pred) * mse.diff(true, pred)b2更新方式:b2 -= lr * sigmoid.diff(pred) * mse.diff(true, pred)
误差传播
既然是误差反向传播,这里仅仅是更新了输出层的参数。而误差还需要继续向前传播,传至隐藏层,以实现隐藏层的参数更新。上文通篇在讲如何对权重(w)求导,而这里所谓的“传播”其实质是对要求导数的参数的某个计算部分中存在关联的参数求导,利用这一计算结果,可以对神经网络前部分的参数继续求导,以实现参数的更新。诶,😞这么说着都好拗口,只恨肚里没墨水,文笔不行呐!😥
下图是完整的神经网络模型的计算过程,链式法则的精髓是对y求导时,y对x导数为x形成y的各个计算部分的导数的乘积(但在矩阵求导中,“乘积”二字变得不太适用,上文内容已经体现出了)
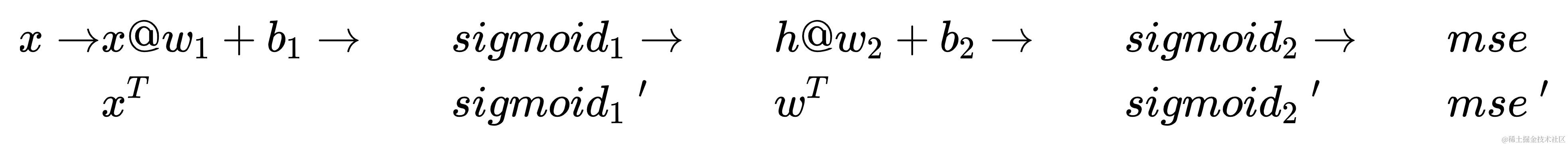
为了对
w
1
w_{1}
w1 求导,根据链式法则,需要先对
s
i
g
m
o
i
d
1
sigmoid_{1}
sigmoid1、
h
@
w
2
+
b
2
h@w_{2}+b_{2}
h@w2+b2、
s
i
g
m
o
i
d
2
sigmoid_{2}
sigmoid2、
m
s
e
mse
mse 这些计算部分求导。其中,
h
@
w
2
+
b
2
h@w_{2}+b_{2}
h@w2+b2 很特殊啊,因为里头的
h
(
即
s
i
g
m
o
i
d
1
)
h\ (即sigmoid_{1})
h (即sigmoid1) 与
w
1
w_{1}
w1 存在关联,也就是说
h
h
h 是
w
1
w_{1}
w1 进行一定运算后的一个计算部分。前面不是有提到“y对x导数为x形成y的各个计算部分的导数”嘛,也正是因此,要对
w
1
w_{1}
w1 求导就必须先对
h
h
h 求导
再来理解理解“对要求导数的参数的某个计算部分中存在关联的参数求导”
- 要求导数的参数就是 w 1 w_{1} w1
- 某个计算部分就是 h @ w 2 + b 2 h@w_{2}+b_{2} h@w2+b2
- 存在关联的参数就是 h h h
这句话其实就是对应了“y对x导数为x形成y的各个计算部分的导数”。好比在上图中,求各个计算部分的导数,就是为了便于求某一参数的导数
隐藏层求导
d l o s s d w 1 \frac{\mathrm{d}\ loss}{\mathrm{d} w_{1}} dw1d loss
对 w 1 w_{1} w1 的求导明显变得复杂了,甚至多了括号。why?因为这可是在矩阵求导,不是标量求导
反正公式在这里了 d a c t i v a t i o n ( x @ w + b ) d x = a c t i v a t i o n ′ @ w t \frac{\mathrm{d}\ activation(x@w+b)}{\mathrm{d} x} = activation\ ' @ w^{t} dxd activation(x@w+b)=activation ′@wt,所以下面的式子中, w 2 t w_{2}^{t} w2t 会出现在最后面,这都与矩阵叉乘的计算方式有关

d l o s s d b 1 \frac{\mathrm{d}\ loss}{\mathrm{d} b_{1}} db1d loss
这个更没必要多说了吧

更新参数
w 1 w_{1} w1 的更新计算方式
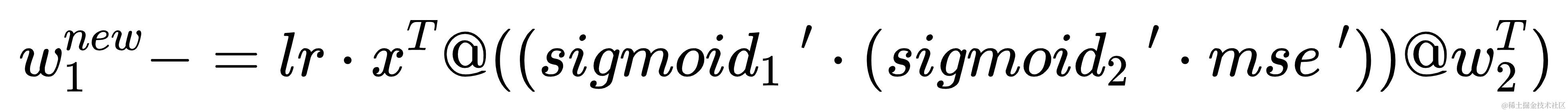
b 1 b_{1} b1 的更新计算方式
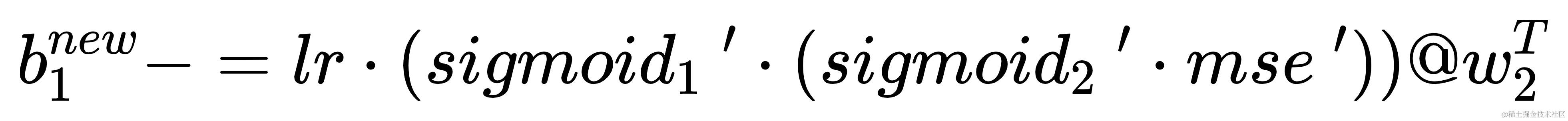
在《手搓神经网络——bp反向传播》- 高级的 bp 反向传播中,故
w1更新方式:w1 -= lr * x.t @ (sigmoid.diff(h) * ((sigmoid.diff(pred) * mse.diff(true, pred)) @ w2.t))b1更新方式:b1 -= lr * (sigmoid.diff(h) * ((sigmoid.diff(pred) * mse.diff(true, pred)) @ w2.t))
in the end
写的又长又臭的,欸哟喂,我的天呐!!!



发表评论