opencv旋转矩形系列(一)
前言
opencv的rotaterect旋转矩形的角度和其构造有关系,构造方法有角度构造、点构造、minarearect()返回旋转矩形,同样的旋转矩形会因为其构造方式不同而有所不同。本文将对三种构建方式进行讲解和测试。
一、rotaterect类
class cv_exports rotatedrect
{
public:
//构造函数
rotatedrect();
rotatedrect(const point2f& center, const size2f& size, float angle);
rotatedrect(const cvbox2d& box);
void points(point2f pts[]) const;//!返回矩形的4个顶点
rect boundingrect() const; //返回包含旋转矩形的最小矩形
operator cvbox2d() const; //!转换到旧式的cvbox2d结构
point2f center; //矩形的质心
size2f size; //矩形的边长
float angle; //旋转角度,当角度为0、90、180、270等时,矩形就成了一个直立的矩形
};
二、按传入角度构造旋转矩形
1.构造函数
rotatedrect(const point2f& center, const size2f& size, float angle);
其中center为传入的旋转矩形中心点坐标,size为旋转矩形宽和高,这里旋转矩形的宽和高并无严格的大小关系,宽度可以大于高度,也可以小于高度,angle为旋转角度,取值范围0到360度,通过其他两种方式获得的旋转矩形,角度的范围与此不同。
2.测试代码
代码如下(示例):
#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;
int main()
{
mat test_image(200, 200, cv_8uc3, scalar(0));
vector<scalar> colors = { scalar(0,0,255),scalar(255,0,255) ,scalar(255,0,0) ,scalar(0,255,0) };
for (int angle = 0; angle < 360; angle += 30)
{
rotatedrect rrect = rotatedrect(point2f(100, 100), size2f(50, 100), angle);
point2f vertices[4];
rrect.points(vertices);
mat temp = test_image.clone();
for (int i = 0; i < 4; i++)
{
line(temp, vertices[i], vertices[(i + 1) % 4], colors[i], 2);
}
string text = "angle: " + to_string(angle);
puttext(temp, text, point(0, 30), font_hershey_simplex, 1.0, scalar(255, 255, 255), 1, 8);
imwrite("./datas/rectangles/" + to_string(angle) + "_rotatedrect.png", temp);
}
return 0;
}
3.测试结果展示
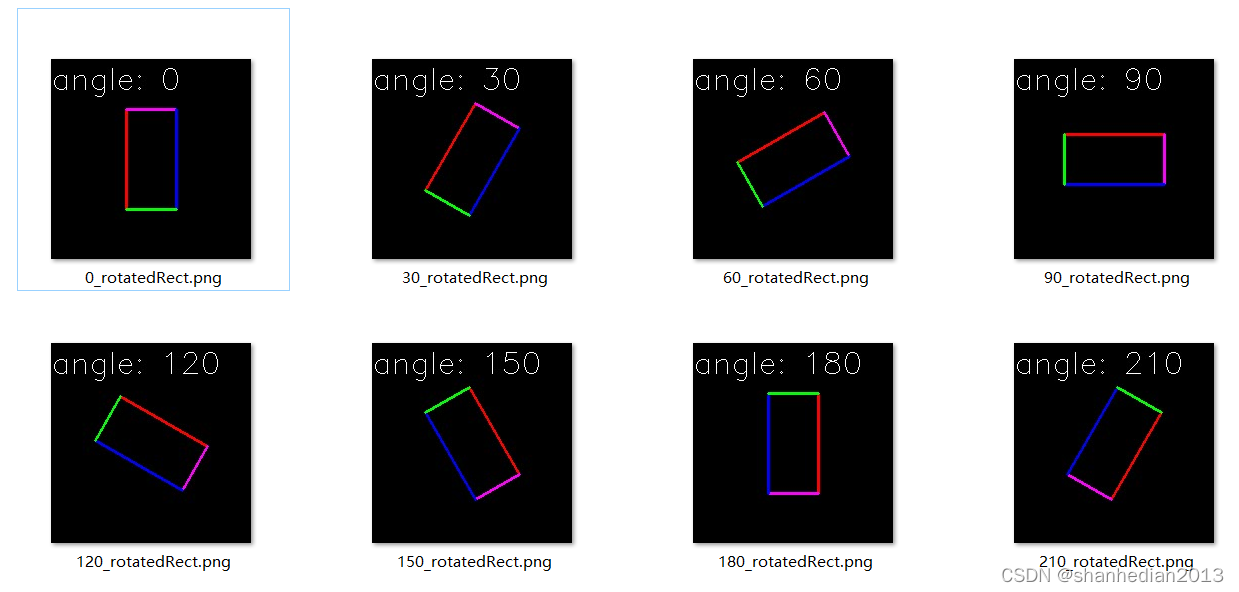
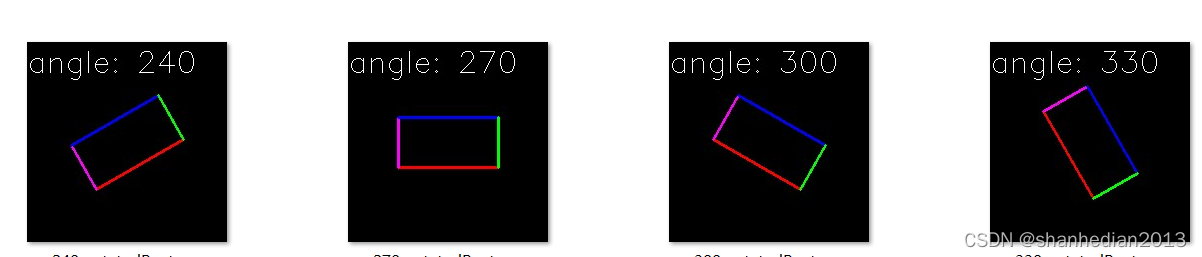
总结
指定旋转中心,旋转角度和宽高创建的旋转矩形,通过上述测试可知,旋转角度指的是宽边和水平向右方向的夹角,且顺时针旋转时角度为正值。## 标题


发表评论