24. 两两交换链表中的节点
定义递归函数swappairs将head之后的节点全部两两交换节点,并且返回交换之后的头结点。
递归出口,如果head==nullptr,此时不需要交换节点,直接返回head。
如果head->next==nullptr,此时只有一个节点,也不需要交换节点,直接返回head。
维护递归函数定义内部逻辑,
listnode* node1 = head->next; listnode* node2 = swappairs(node1->next);
首先记录这两个需要修改链节的结点。 node1->next = head; head->next = node2;
交换节点过程。
return node1;
返回交换之后的头结点。
/**
* definition for singly-linked list.
* struct listnode {
* int val;
* listnode *next;
* listnode() : val(0), next(nullptr) {}
* listnode(int x) : val(x), next(nullptr) {}
* listnode(int x, listnode *next) : val(x), next(next) {}
* };
*/
class solution {
public:
listnode* swappairs(listnode* head) {
if (head == nullptr || head->next == nullptr)
return head;
listnode* node1 = head->next;
listnode* node2 = swappairs(node1->next);
node1->next = head;
head->next = node2;
return node1;
}
};时间复杂度分析:
t(n)=t(n-1)+o(1)=.....=t(1)+n*o(1)=o(n)
在每一次调用swappairs函数时,都会进行一次交换操作,这需要常数级时间复杂度。
对于长度为n的链表,每次调用swappairs都会递归调用swappairs函数处理链表剩余部分,直到到达链表末尾或只剩下一个节点。因此,总体上每个节点都会被访问一次,时间复杂度为o(n)。
空间复杂度分析:
递归调用swappairs函数会使用系统栈空间,其空间复杂度为o(n)。这是因为在递归的过程中,系统需要为每一层递归调用保存当前的状态信息(如局部变量、返回地址等),直到递归到链表末尾才会释放这些信息。
此外,由于递归调用时并没有使用额外的数据结构来存储节点信息,而是直接在原链表上进行操作,因此除了系统栈空间外,并不会额外消耗其他空间。
因此,该函数的时间复杂度为o(n),空间复杂度为o(n)。
50. pow(x, n)
定义递归函数mypow计算x的n次方。
递归函数的内部逻辑,计算x的n/2次方,如果n%2==0,说明mypow(x,n)==mypow(x,n/2)*mypow(x,n/2)。
如果n%2!=0,说明mypow(x,n)==mypow(x,n/2)*mypow(x,n/2)*x。
递归函数的内部逻辑,n==0时,返回1。当然,n==1时,返回x。
处理细节,如果n<0,转化计算,因为我们默认n是大于0的,小于0只需要转换一下即可。
class solution {
public:
double mypow(double x, long long n) {
// 定义递归函数mypow计算x的n次方
if (n == 1)
return x;
if (n == 0)
return 1;
if (n < 0)
return 1.0 / mypow(x, -n);
double tmp = mypow(x, n / 2);
return n % 2 == 0 ? tmp * tmp : tmp * tmp * x;
}
};时间复杂度分析:
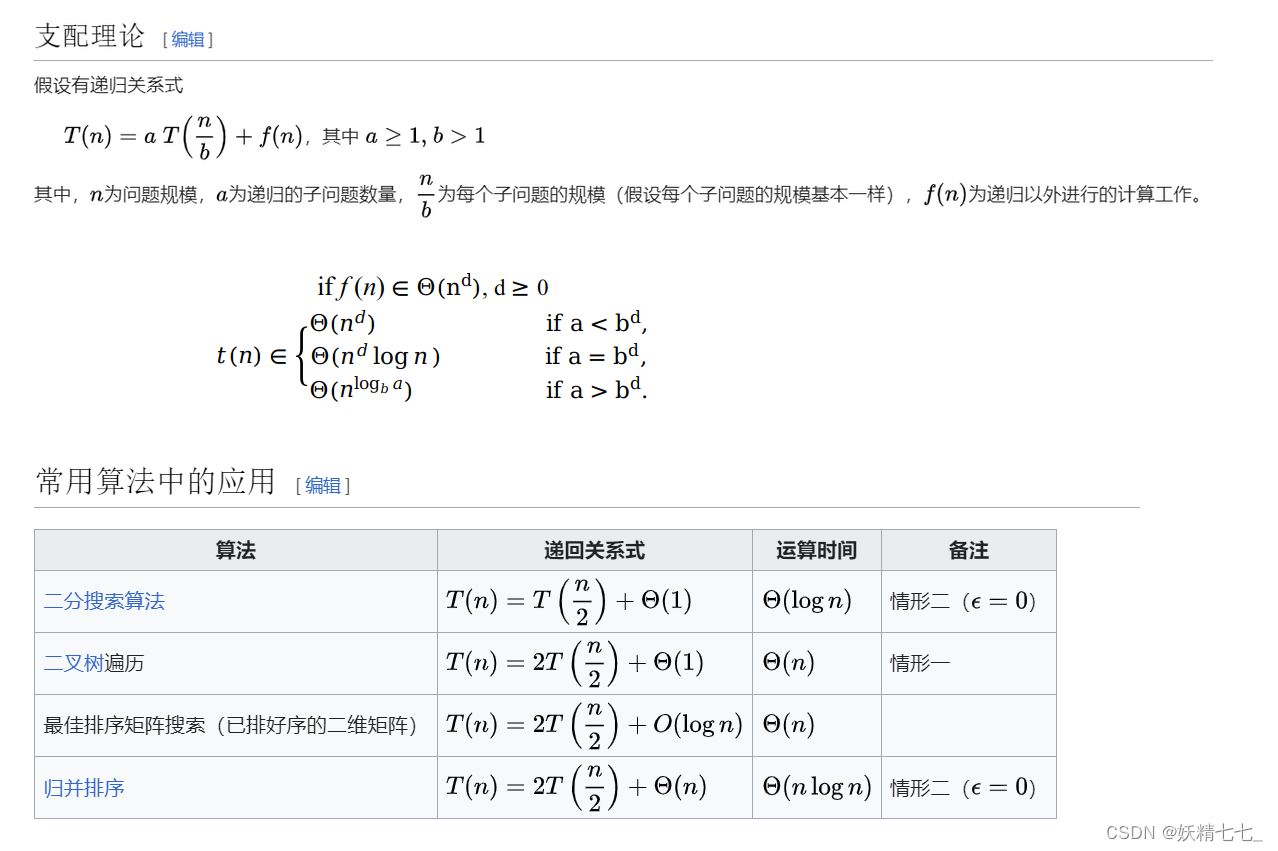
t(n)=t(n/2)+o(1)
a=1,b=2,d=0,k=0。
其中a=b^k。
发现d==k,说明t(n)=n^d*logn=logn。
由于在每次调用mypow时,都会将n减半,因此在递归的过程中,n的规模每次都会减半。因此,整个算法的时间复杂度可以表示为o(log n)。
在每次递归调用中,会进行一次除法运算(n/2)和一次取模运算(n%2),这些基本操作的时间复杂度为o(1)。
因此,整个算法的时间复杂度主要由递归的深度决定,为o(log n)。
空间复杂度分析:
递归函数mypow的递归调用会使用系统栈空间来存储每一层递归的状态信息,因此空间复杂度取决于递归的深度。
在本算法中,由于每次n都会减半,递归树的深度为o(log n),因此空间复杂度也为o(log n)。
此外,除了系统栈空间外,并没有使用额外的数据结构存储节点信息,因此除了系统栈空间外,并不会额外消耗其他空间。
因此,该函数的时间复杂度为o(log n),空间复杂度为o(log n)。
结尾
最后,感谢您阅读我的文章,希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点,请随时在评论区留言。
同时,不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中,我将继续探讨这个话题的不同方面,为您呈现更多深度和见解。
谢谢您的支持,期待与您在下一篇文章中再次相遇!



发表评论