【自然语言处理】【大模型】DeepSeek-V2论文解析

论文地址：https://arxiv.org/pdf/2405.04434

一、简介

• deepseek-v2是一个总参数为236b的moe模型，每个token仅激活21b的参数，并支持128k的上下文长度。
• 提出了multi-head latent attention(mla)，通过压缩kv cache至隐向量，从而保证高效推理。
• 相比于deepseek 67b，deepseek-v2实现了更好的表现，节约了42.5%的训练成本，降低了93.3%的kv cache，提升最大吞吐5.76倍。
• 预训练语料包含了8.1t tokens并进一步进行sft和rl。

二、模型结构

1. mla(multi-head latent attention)

​ 传统transformer采用mha(multi-head attention)，但是kv cache会成为推理瓶颈。mqa(multi-query attention)和gqa(grouped-query attention)可以一定程度减少kv cache，但效果上不如mha。deepseek-v2设计了一种称为mla(multi-head latent attention)的注意力机制。mla通过低秩key-value联合压缩，实现了比mha更好的效果并且需要的kv cache要小很多。

1.1 标准mha

​ 令$d$为embedding维度，$n_h$是注意力头的数量，$d_h$是每个头的维度，${\text{h}}_t\in {\mathbb{r}}^d$是注意力层中第$t$个token的输入。标准mha通过三个矩阵$w^q,w^k,w^v\in {\mathbb{r}}^{d_h{n}_h\times d}$来产生${\text{q}}_t,{\text{k}}_t,{\text{v}}_t\in {\mathbb{r}}^{d_h{n}_h}$。
$$\begin{array}{rl}{\text{q}}_t& =w^q{\text{h}}_t\\ {\text{k}}_t& =w^k{\text{h}}_t\\ {\text{v}}_t& =w^v{\text{h}}_t\end{array}\text{\hspace{1em}(1)(2)(3)}$$
在mha中${\text{q}}_t,{\text{k}}_t,{\text{v}}_t$会被划分为$n_h$个头：
$$\begin{array}{rl}& [{\text{q}}_{t,1};{\text{q}}_{t,2};\dots ,{\text{q}}_{t,n_h}]={\text{q}}_t\\ & [{\text{k}}_{t,1};{\text{k}}_{t,2};\dots ,{\text{k}}_{t,n_h}]={\text{k}}_t\\ & [{\text{v}}_{t,1};{\text{v}}_{t,2};\dots ,{\text{v}}_{t,n_h}]={\text{v}}_t\\ & {\text{o}}_{t,i}=\sum _{j=1}^t\text{softmax}(\frac{{\text{q}}_{t,i}^{\top }{\text{k}}_{j,i}}{\sqrt{d_h}}){\text{v}}_{j,i}\\ & {\text{u}}_t=w^o[{\text{o}}_{t,1};{\text{o}}_{t,2};\dots ,{\text{o}}_{t,n_h}]\end{array}\text{\hspace{1em}(4)(5)(6)(7)(8)}$$
其中${\text{q}}_{t,i},{\text{k}}_{t,i},{\text{v}}_{t,i}\in {\mathbb{r}}^{d_h}$是第$i$个注意力头的query、key和value，$w^o\in {\mathbb{r}}^{d\times d_h{n}_h}$是输出投影矩阵。在推理时，所有的key和value都会被缓存来加速推理。对于每个token，mha需要缓存$2n_h{d}_{h}l$个元素。

1.2 低秩key-value联合压缩

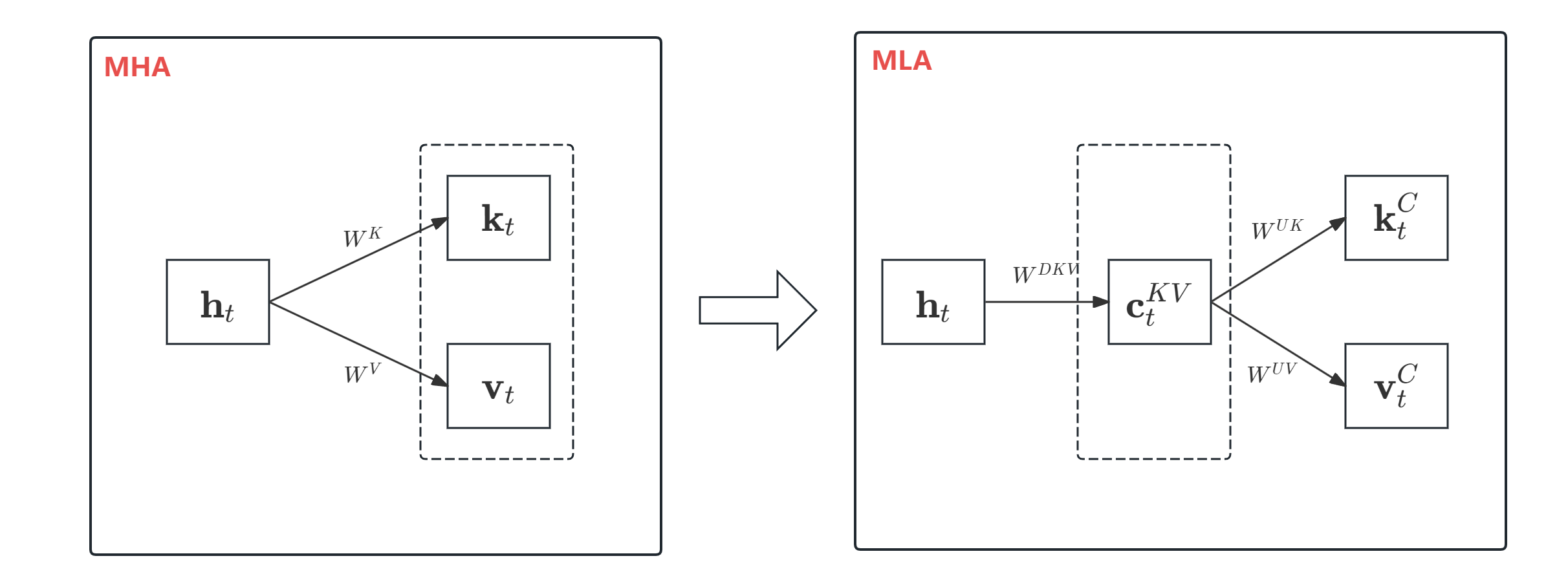
​ mla通过低秩联合压缩key和value来减少kv cache：
$$\begin{array}{rl}{\text{c}}_t^{kv}& =w^{dkv}{\text{h}}_t\\ {\text{k}}_t^c& =w^{uk}{\text{c}}_t^{kv}\\ {\text{v}}_t^c& =w^{uv}{\text{c}}_t^{kv}\end{array}\text{\hspace{1em}(9)(10)(11)}$$
其中${\text{c}}_t^{kv}\in {\mathbb{r}}^{d_c}$是用于压缩key和value的隐向量；$d_c(\ll d_h{n}_h)$表示kv压缩的维度；$w^{dkv}\in {\mathbb{r}}^{d_c\times d}$是下投影矩阵，$w^{uk},w^{uv}\in {\mathbb{r}}^{d_h{n}_h\times d_c}$表示上投影矩阵。在推理时，mla仅需要缓存${\text{c}}_t^{kv}$，因此kv cache仅需要缓存$d_{c}l$个元素。此外，在推理时可以把$w^{uk}$吸收到$w^q$，$w^{uv}$吸收到$w^o$中，这样甚至都不需要计算key和value。

​ 此外，为了在训练时降低激活的显存占用，对query也进行低秩压缩，即使其不能降低kv cache。具体来说，
$$\begin{array}{rl}{\text{c}}_t^q& =w^{dq}{\text{h}}_t\\ {\text{q}}_t^c& =w^{uq}{\text{c}}_t^q\end{array}\text{\hspace{1em}(12)(13)}$$
其中${\text{c}}_t^q\in {\mathbb{r}}^{d_c^{\prime }}$是query的压缩后隐向量；$d_c^{\prime }(\ll d_h{n}_h)$表示query的压缩维度；$w^{dq}\in {\mathbb{r}}^{d_c^{\prime }\times d},w^{uq}\in {\mathbb{r}}^{d_h{n}_h\times d_c^{\prime }}$是下投影矩阵和上投影矩阵。

1.3 解耦rope

​ rope与低秩kv压缩并不兼容。具体来说，rope对于query和key是位置敏感的。若将rope应用在${\text{k}}_t^c$上，等式10中的$w^{uk}$将与位置敏感rope矩阵耦合。但是在推理时，$w^{uk}$就无法被吸收到$w^q$中，因为对当前生成token相关的rope矩阵将位于$w^q$和$w^{uk}$之间，而矩阵乘法不满足交换律。因此，推理时必须重新计算前面token的key，这会显著影响推理效率。

​ 为了解决这个问题，提出使用额外的多头query ${\text{q}}_{t,i}^r\in {\mathbb{r}}^{d_h^r}$和共享key ${\text{k}}_t^r\in {\mathbb{r}}^{d_h^r}$来携带rope，其中$d_h^r$表示解耦query和key的每个头的维度。在mla中使用解耦rope策略的方式为：
$$\begin{array}{rl}{\text{q}}_t^r& =[{\text{q}}_{t,1}^r;{\text{q}}_{t,2}^r;\dots ;{\text{q}}_{t,n_h}^r]=\text{rope}(w^{qr}{\text{c}}_t^q)\\ {\text{k}}_t^r& =\text{rope}(w^{kr}{\text{h}}_t)\\ {\text{q}}_{t,i}& =[{\text{q}}_{t,i}^c;{\text{q}}_{t,i}^r]\\ {\text{k}}_{t,i}& =[{\text{k}}_{t,i}^c;{\text{k}}_t^r]\\ {\text{o}}_{t,i}& =\sum _{j=1}^t{\text{softmax}}_j(\frac{{\text{q}}_{t,i}^{\top }{\text{k}}_{j,i}}{\sqrt{d_h+d_h^r}}){\text{v}}_{j,i}^c\\ {\text{u}}_t& =w^o[{\text{o}}_{t,1};{\text{o}}_{t,2};\dots ;{\text{o}}_{t,n_h}]\end{array}\text{\hspace{1em}(14)(15)(16)(17)(18)(19)}$$
其中$w^{qr}\in {\mathbb{r}}^{d_h^r{n}_h\times d_c^{\prime }}$和$w^{kr}\in {\mathbb{r}}^{d_h^r\times d}$是用于产生解耦query和key的矩阵；$\text{rope}(\cdot )$表示应用rope的操作；$[\cdot ;\cdot ]$表示拼接操作。在推理时，解耦的key也需要被缓存。因此，deekseek-v2需要的总kv cache包含$(d_c+d_h^r)l$个元素。

1.4 结论

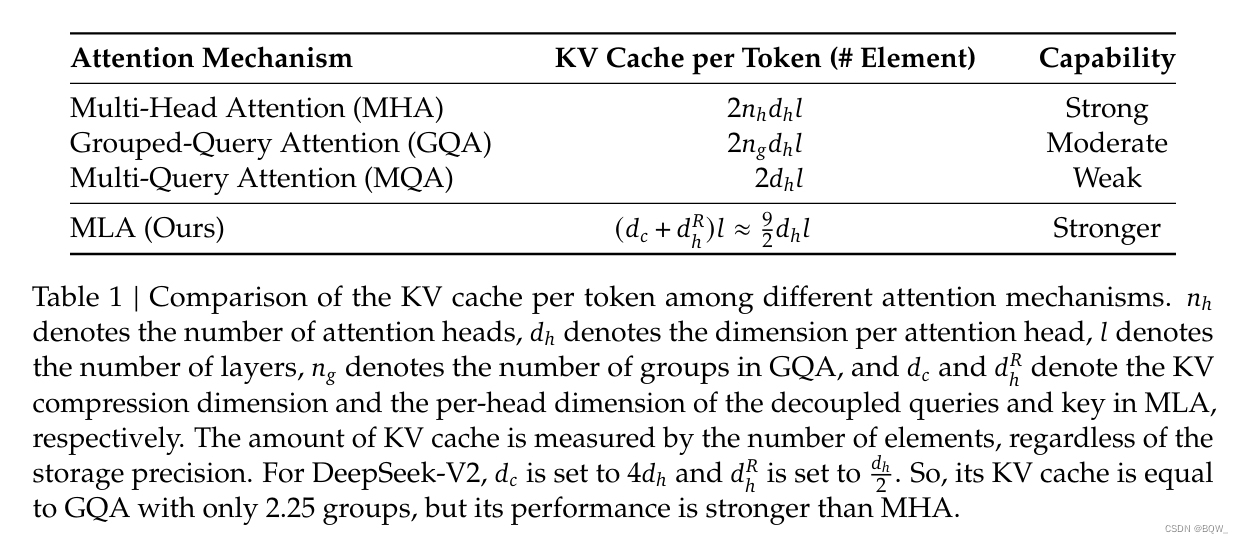
​ mla能够通过更少的kv cache实现比mha更好的效果。

2. 整体结构

2.1 基础结构

​ 对于ffn层，利用deepseekmoe架构，即将专家划分为更细粒度，从而获得更专业化的专家以及获取更准确的知识。在具有相同激活和总专家参数的情况下，deepseekmoe能够大幅度超越传统moe架构。

​ 令${\text{u}}_t$是第t个token对ffn的输入，那么计算ffn的输出${\text{h}}_t^{\prime }$为：
h t ′ = u t + ∑ i = 1 n s ffn i ( s ) ( u t ) + ∑ i = 1 n r g i , t ffn i ( r ) ( u t ) g i , t = { s i , t , s i , t ∈ topk ( { s j , t ∣ 1 ≤ j ≤ n r } , k r ) 0 , otherwise s i , t = softmax i ( u t ⊤ e i ) \begin{align} \textbf{h}_t'&=\textbf{u}_t+\sum_{i=1}^{n_s}\text{ffn}_i^{(s)}(\textbf{u}_t)+\sum_{i=1}^{n_r}g_{i,t}\text{ffn}_{i}^{(r)}(\textbf{u}_t) \tag{20}\\ g_{i,t}&=\begin{cases} s_{i,t},& s_{i,t}\in\text{topk}(\{s_{j,t}|1\leq j\leq n_r\},k_r)\\ 0,&\text{otherwise} \end{cases}\tag{21}\\ s_{i,t}&=\text{softmax}_i(\textbf{u}_t^\top \textbf{e}_i) \tag{22}\\ \end{align} \\ ht′​gi,t​si,t​​=ut​+i=1∑ns​​ffni(s)​(ut​)+i=1∑nr​​gi,t​ffni(r)​(ut​)={si,t​,0,​si,t​∈topk({sj,t​∣1≤j≤nr​},kr​)otherwise​=softmaxi​(ut⊤​ei​)​(20)(21)(22)​
其中$n_s$和$n_r$表示共享专家和路由专家的数量；${\text{ffn}}_i^{(s)}(\cdot )$和${\text{ffn}}_i^{(r)}(\cdot )$表示第i个共享专家和第i个路由专家；$k_r$表示激活路由专家的数量；$g_{i,t}$是第i个专家的门限值；${\text{e}}_i$是当前层第i个路由专家的中心。

2.2 设备受限路由

​ 设计了一种设备受限路由机制来控制moe相关的通信成本。当采用专家并行时，路由专家将分布在多个设备上。对于每个token，moe相关的通信频率与目标专家覆盖的设备数量成正比。由于在deepseekmoe中细粒度专家划分，激活专家的数量会很大，因此应用专家并行时，与moe相关的通信将更加昂贵。

​ 对于deepseek-v2，除了路由专家会选择top-k个以外，还会确保每个token的目标专家最多分布在m个设备上。具体来说，对于每个token，先选择包含最高分数专家的m个设备。然后在这m个设备上执行top-k选择。在实践中，当$m\ge 3$时，设备受限路由能够实现与不受限top-k路由大致一致的良好性能。

2.3 用于负载均衡的辅助loss

​ 不平衡的负载会增加路由坍缩的风险，使一些专家无法得到充分的训练和利用。此外，当使用专家并行时，不平衡的负载降低计算效率。在deepseek-v2训练时，设计了三种辅助损失函数用于控制专家级别负载均衡$({\mathcal{l}}_{\text{expbal}})$、设备级别负载均衡$({\mathcal{l}}_{\text{devbal}})$和通信均衡${\mathcal{l}}_{\text{commbal}}$。

​ 专家级均衡loss。专家级均衡loss用于缓解路由坍缩问题：
$$\begin{array}{rl}{\mathcal{l}}_{\text{expbal}}& ={\alpha }_1\sum _{i=1}^{n_r}{f}_i{p}_i,\\ f_i& =\frac{n_r}{k_{r}t}\sum _{t=1}^{t}1\text{(token t selects expert i)}\\ p_i& =\frac{1}{t}\sum _{t=1}^t{s}_{i,t}\end{array}\text{\hspace{1em}(23)(24)(25)}$$
其中${\alpha }_1$是称为专家级均衡因子的超参数；$1(\cdot )$是指示函数；$t$是序列中token的数量。

​ 设备级均衡loss。除了专家级均衡loss以外，也设计了设备级别均衡loss来确保跨设备均衡计算。在deepseek-v2训练过程中，将所有的专家划分至$d$组 { e 1 , e 2 , … , e d } \{\mathcal{e}_1,\mathcal{e}_2,\dots,\mathcal{e}_d\} {e1​,e2​,…,ed​}并在单个设备上部署每个组。设备级均衡loss计算如下：
$$\begin{array}{rl}{\mathcal{l}}_{\text{devbal}}& ={\alpha }_2\sum _{i=1}^d{f}_i^{\prime }{p}_i^{\prime }\\ f_i^{\prime }& =\frac{1}{{\mathcal{e}}_i}\sum _{j\in {\mathcal{e}}_i}{f}_j\\ p_i^{\prime }& =\sum _{j\in {\mathcal{e}}_i}{p}_j\end{array}\text{\hspace{1em}(26)(27)(28)}$$
其中${\alpha }_2$是称为设备级均衡因子的超参数。

​ 通信均衡loss。通信均衡loss能够确保每个设备通信的均衡。虽然设备限制路由机制能够确保每个设备发送信息有上限，但是当某个设备比其他设备接收更多的tokens，那么实际通信效率将会有影响。为了缓解这个问题，设计了一种通信均衡loss如下：
$$\begin{array}{rl}{\mathcal{l}}_{\text{commbal}}& ={\alpha }_3\sum _{t=1}^d{f}_i^{\prime \prime }{p}_i^{\prime \prime }\\ f_i^{\prime \prime }& =\frac{d}{mt}\sum _{t=1}^{t}1\text{(token t is sent to device i)}\\ p_i^{\prime \prime }& =\sum _{j\in {\mathcal{e}}_i}{p}_j\end{array}\text{\hspace{1em}(29)(30)(31)}$$
其中${\alpha }_3$是称为通信均衡因子的超参数。设备受限路由机制操作主要确保每个设备至多向其他设备传输mt个hidden states。同时，通信均衡loss用来鼓励每个设备从其他设备接受mt个hidden states。通信均衡loss确保设备间信息均衡交换，实现高效通信。

2.4 token-dropping策略

​ 虽然均衡loss的目标是确保均衡负载，但是其并不能严格确保负载均衡。为了进一步缓解由于不均衡导致的计算浪费，在训练时引入了设备级别的token-dropping策略。该方法会先计算每个设备的平均计算预算，这意味着每个设备的容量因子等于1.0。然而，在每个设备上drop具有最低affinity分数的token，直到达到计算预算。此外，确保大约10%的训练序列的token永远不会被drop。这样，可以根据效率要求灵活地决定是否在推理过程中drop token，并确保训练和推理的一致性。

三、预训练

1. 实验设置

1.1 数据构造

​ 数据处理过程同deepseek 67b，并进一步扩展数据量和质量。采用与deepseek 67b相同的tokenizer。预训练语料包含8.1t tokens，中文token比英文多12%。

1.2 超参数

​ 略

1.3 infrastructures

​ deepseek-v2训练基于hai-llm框架。利用16路0气泡流水并行、8路专家并行和zero-1数据并行。考虑到deepseek-v2具有相对较少的激活参数，并且对一部分操作进行重计算来节约激活显存，因此可以不使用张量并行，从而降低通信开销。此外，为了进一步提高训练效率，使用专家并行all-to-all通信来重叠共享专家的计算。使用定制化的cuda核来改善通信、路由算法和不同专家之间融合线性计算。此外，mla基于改善版本的flashattention-2进行优化。

1.4 长上下文扩展

​ 使用yarn将上下文窗口尺寸从4k扩展至128k。

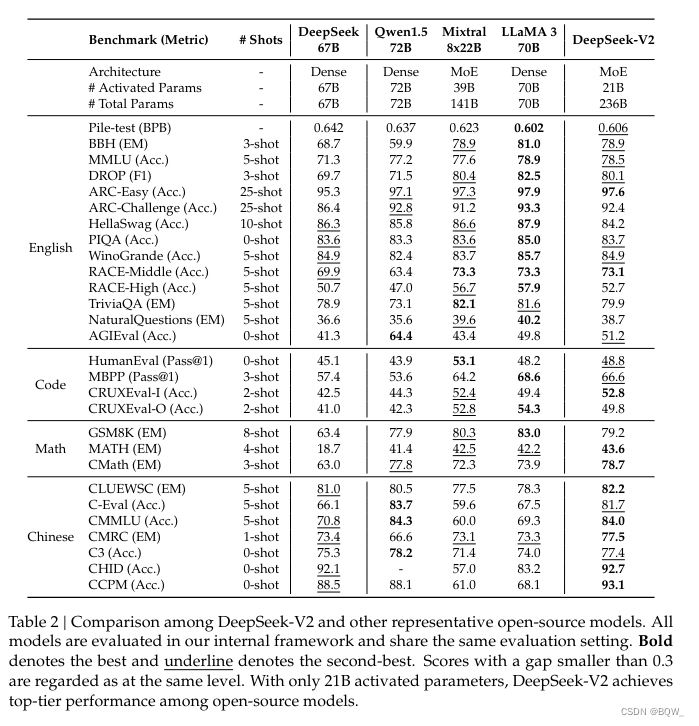
2. 评估

四、对齐

​ sft。 使用了150万样本的微调数据，其中120万是用于有用性，30万则用于安全性。

​ 强化学习。仍然采用grpo。

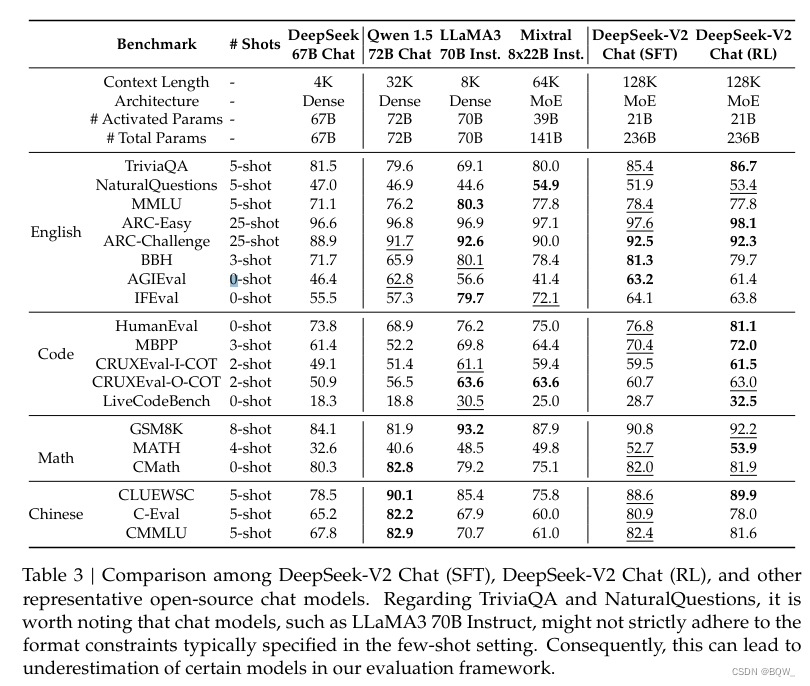
​ 结果。