DFS：二叉树的深搜与回溯

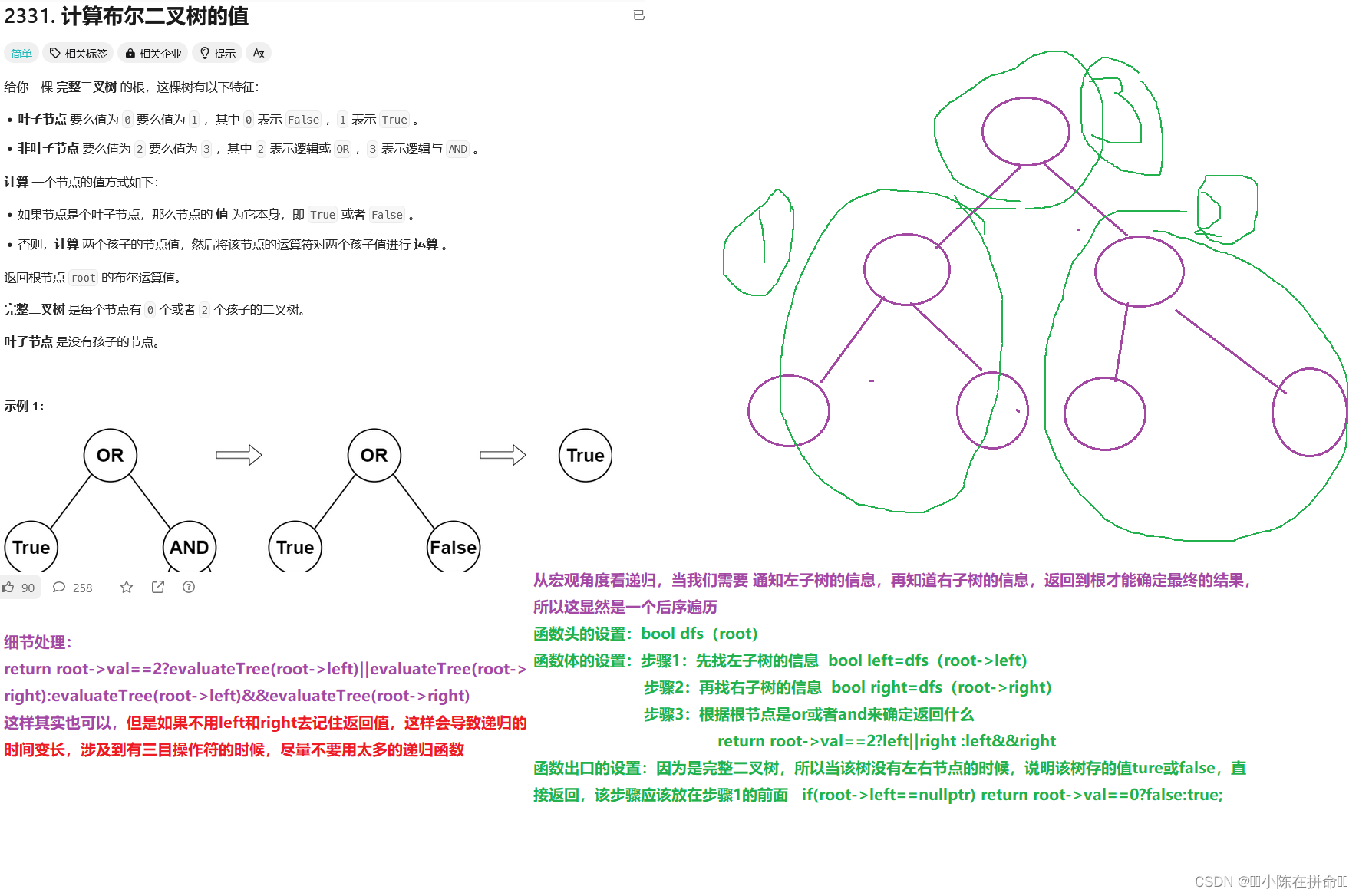
   一、计算布尔二叉树的值

. - 力扣（leetcode）

class solution {
public:
    bool evaluatetree(treenode* root) 
    {
      if(root->left==nullptr) return root->val==0?false:true; 
      bool left= evaluatetree(root->left);
      bool right=evaluatetree(root->right);
      return root->val==2?left||right:left&&right;
      //直接return root->val==2?evaluatetree(root->left)||evaluatetree(root->right):evaluatetree(root->left)&&evaluatetree(root->right)  会导致递归的时间变长，因为我们没有去记住返回值，所以一旦需要就得重新递归回去计算
    }
};

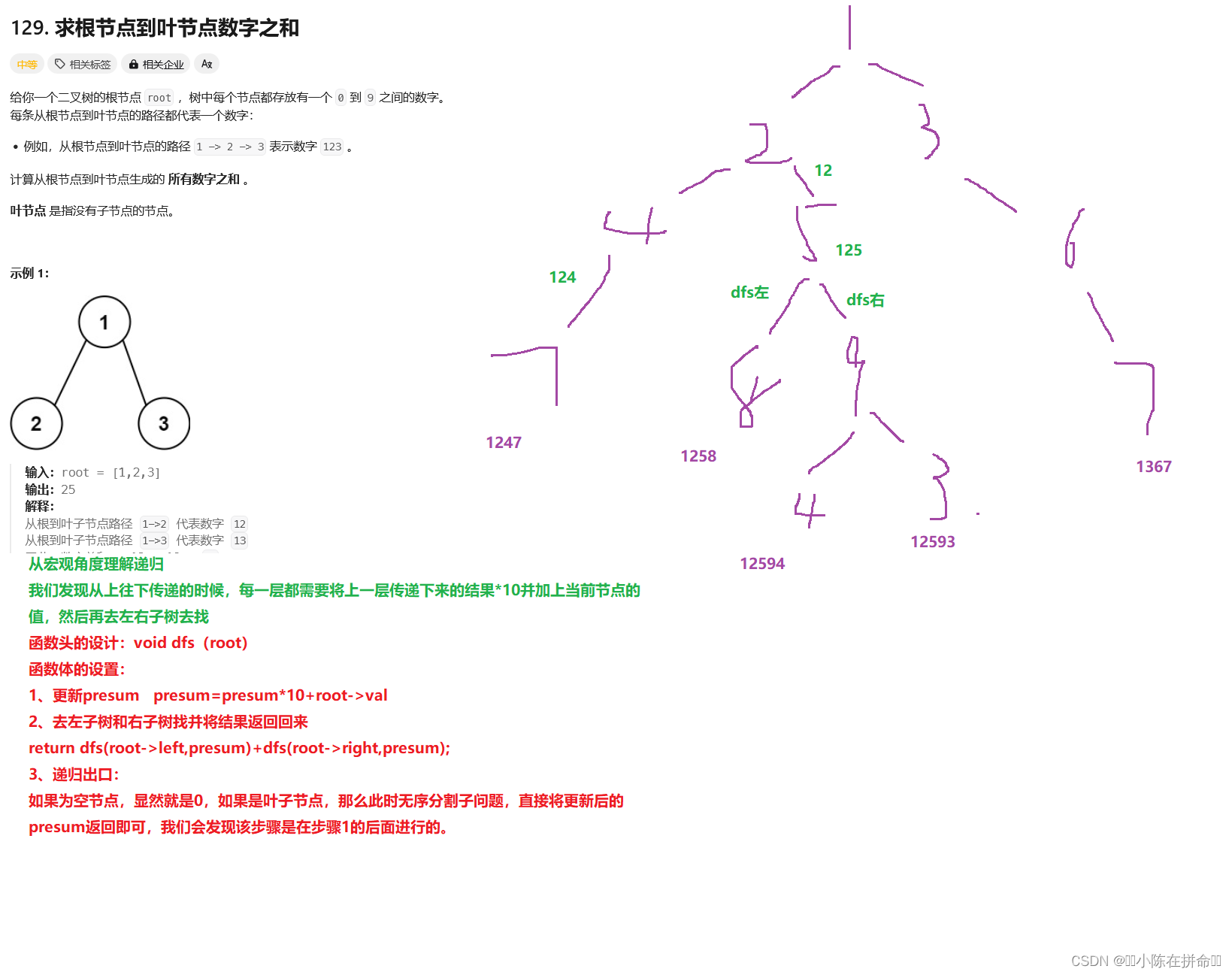
二、求根节点到叶节点的数字之和

. - 力扣（leetcode）

class solution {
public:
     int dfs(treenode* root,int presum)//presum也是为了回溯
     {
        if(root==nullptr) return 0;
        presum=10*presum+root->val;//因为不管怎么样都得加
        if(root->left==nullptr&&root->right==nullptr) return presum;
        //此时如果左右不为空，加上这个结果
         return dfs(root->left,presum)+dfs(root->right,presum);
     }
     int sumnumbers(treenode* root) 
    {  
        return dfs(root,0);
    }
};

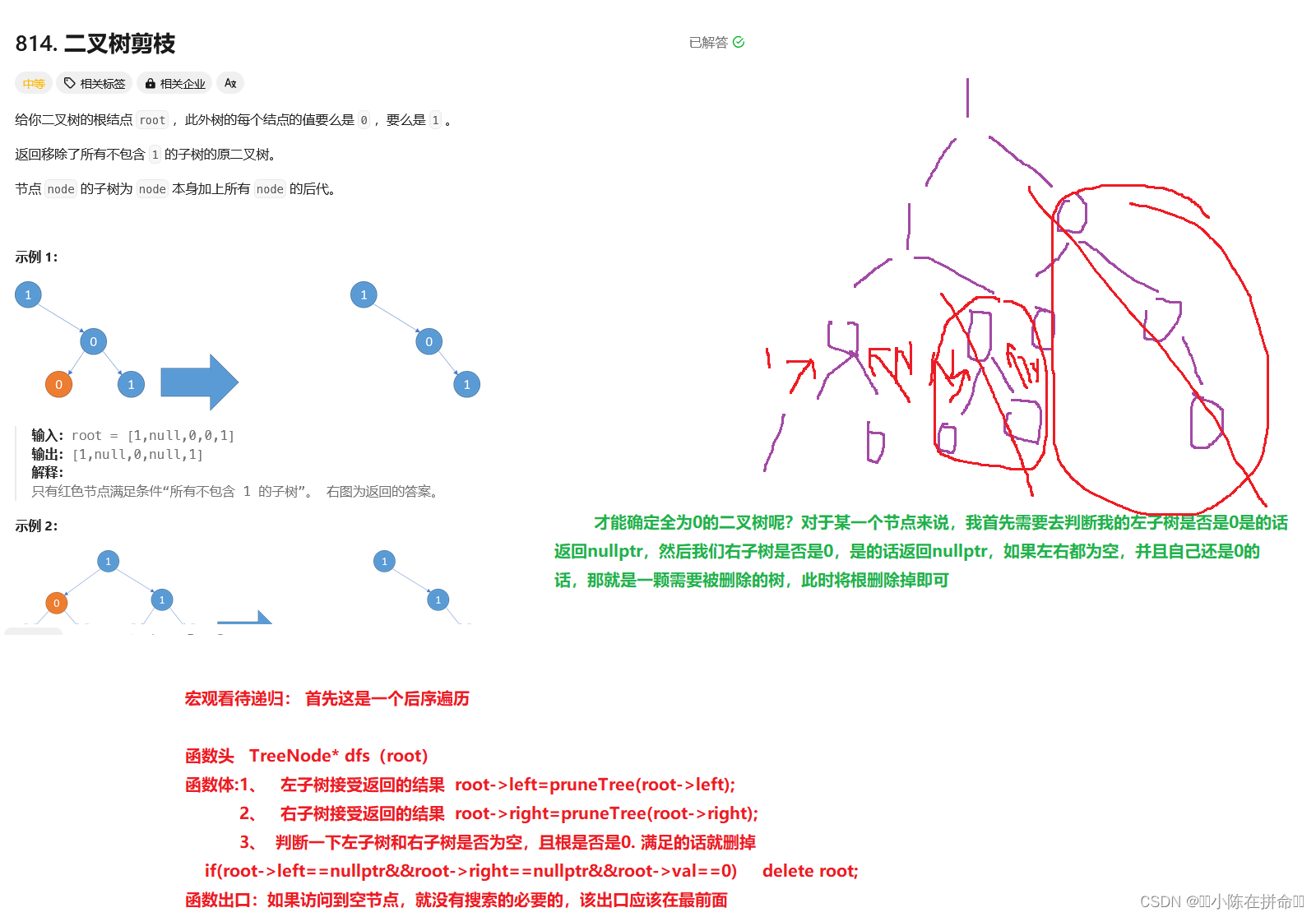
三、二叉树剪枝

. - 力扣（leetcode）

class solution {
public:
    treenode* prunetree(treenode* root) 
    {
        if(root==nullptr) return nullptr;
        root->left=prunetree(root->left);
        root->right=prunetree(root->right);
        if(root->left==nullptr&&root->right==nullptr&&root->val==0)     delete root;
        return root;
    }
};

四、 验证二叉搜索树

 . - 力扣（leetcode）

class solution {
public:
    long prev=long_min;//比负无穷还小
    bool isvalidbst(treenode* root) 
    {
       if(root==nullptr) return true;//为空的话是符合条件的
      //进行中序遍历
      bool l=isvalidbst(root->left);//先找左子树
      if(l==false) return false;//减枝（大多数的减枝就只是一个条件判断）
      bool temp=(prev<root->val);//判断当前是否大于前驱
      if(temp==false) return false;//减枝
      prev=root->val;//更新前驱
      bool r=isvalidbst(root->right);//再找右子树
      return r;
    }
};

五、二叉搜索树中第k小的节点

. - 力扣（leetcode）

class solution {
public:
    int count=0;
    int ret=0;
    int kthsmallest(treenode* root, int k) 
    {
      count=k;
      dfs(root);
      return ret;
    }
    void dfs(treenode* root)
    {
        if(root==nullptr) return;
        dfs(root->left);
        //中序遍历
        if(--count==0) {ret=root->val; return;}//if判断也是剪枝
        dfs(root->right);
    }
};

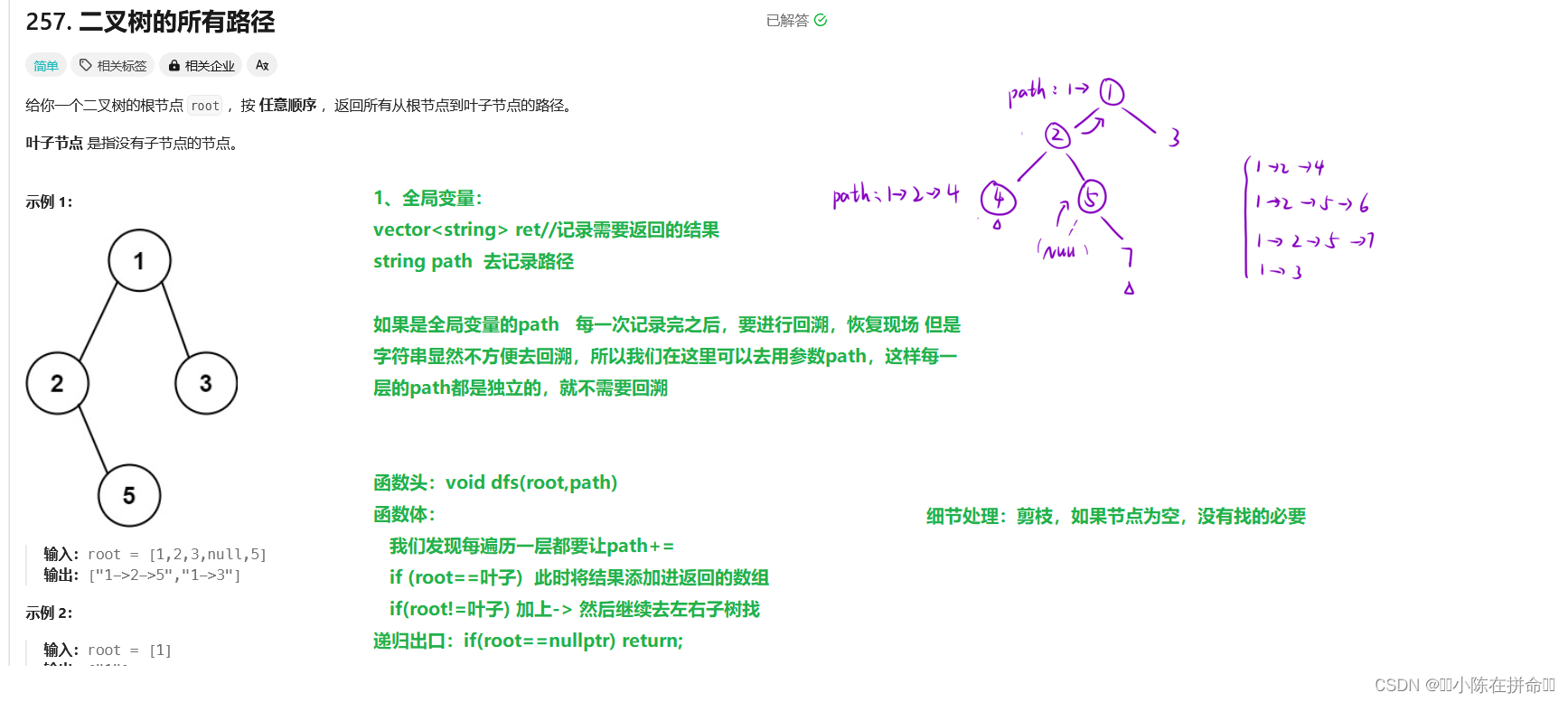
 六、二叉树的所有路径

class solution {
public:
    vector<string> ret;//利用全局变量来存储我们返回的结果
    void dfs(treenode* root,string path)
    {
      if(root==nullptr) return;//为空 啥也不干  
      path+=to_string(root->val);//不为空的话，把自己给加上
      if(root->left==nullptr&&root->right==nullptr) 
        ret.push_back(path); //如果是叶子节点，返回最终结果
      else //不是叶子节点的话，继续往后找
      {
        path+="->";
        //继续去左右子树去找
        dfs(root->left,path);
        dfs(root->right,path);
      }
    }
    vector<string> binarytreepaths(treenode* root) 
    {
        dfs(root,"");
        return ret;
    }
};

 七、路径总和2

. - 力扣（leetcode）

思路1：全局path+回溯 

class solution {
public:
    vector<vector<int>> ret;
    vector<int> path;
    vector<vector<int>> pathsum(treenode* root, int targetsum) 
    {
       dfs(root,targetsum);
       return ret;
    }
    void dfs(treenode* root,int targetsum)
    {
        if(root==nullptr) return;
        //if(targetsum<0) return;有负数，所以不能剪枝
        targetsum-=root->val;
        path.push_back(root->val);
        if(root->left==nullptr&&root->right==nullptr&&targetsum==0) {ret.push_back(path);return;}
        dfs(root->left,targetsum);
        if(root->left)  path.pop_back();
        dfs(root->right,targetsum);
        if(root->right)  path.pop_back();
    }
};

思路2：形参path记录路径结果

class solution {
public:
    vector<vector<int>> ret;
    vector<vector<int>> pathsum(treenode* root, int targetsum) 
    {
       dfs(root,targetsum,{});
       return ret;
    }
    void dfs(treenode* root,int targetsum,vector<int> path)
    {
        if(root==nullptr) return;
        targetsum-=root->val;
        path.push_back(root->val);
        if(root->left==nullptr&&root->right==nullptr&&targetsum==0) ret.push_back(path);
        dfs(root->left,targetsum,path);
        dfs(root->right,targetsum,path);
    }
};

八、从叶节点开始的最小字符串 

. - 力扣（leetcode）

思路1：全局path+回溯

class solution {
public:
    string minpath;
    string path;
    string smallestfromleaf(treenode* root) 
    {
        dfs(root);
       return minpath;
    }
    void dfs(treenode* root)
    {
        if(root==nullptr) return;
        //先加上对应的节点
        path=char(root->val+'a')+path;
        //如果是叶子节点，那么就和minpath进行比较，小的话更新
        if(root->left==nullptr&&root->right==nullptr)//是叶子，就要进行比较
        if(minpath.empty()||minpath>path) //为空的时候，也要更新
            minpath=path;//更新
        //没找到，就去左右子树找
        dfs(root->left);
        if(root->left) path.erase(path.begin());
        dfs(root->right);
        if(root->right) path.erase(path.begin());
    }
};

思路2：参数path记录路径结果 

class solution {
public:
    string minpath;
    string smallestfromleaf(treenode* root) 
    {
        dfs(root,"");
       return minpath;
    }
    void dfs(treenode* root,string path)
    {
        if(root==nullptr) return;
        //先加上对应的节点
        path=char(root->val+'a')+path;
        //如果是叶子节点，那么就和minpath进行比较，小的话更新
        if(root->left==nullptr&&root->right==nullptr)//是叶子，就要进行比较
        if(minpath.empty()||minpath>path) //为空的时候，也要更新
            minpath=path;//更新
        //没找到，就去左右子树找
        dfs(root->left,path);
        dfs(root->right,path);
    }
};