📚博客主页:zhui_yi_
🔍:上期回顾:
❤️感谢大家点赞👍🏻收藏⭐评论✍🏻,您的三连就是我持续更新的动力❤️
🎇追当今朝天骄,忆顾往昔豪杰。

文章目录
前言
本期我将带来图的应用,包括最小生成树、最短路径、拓扑排序、关键路径。
一、最小生成树
引入以及复习
在理解最小生成树的时候,我们先了解一下生成树。
那么什么是极小连通子图呢?
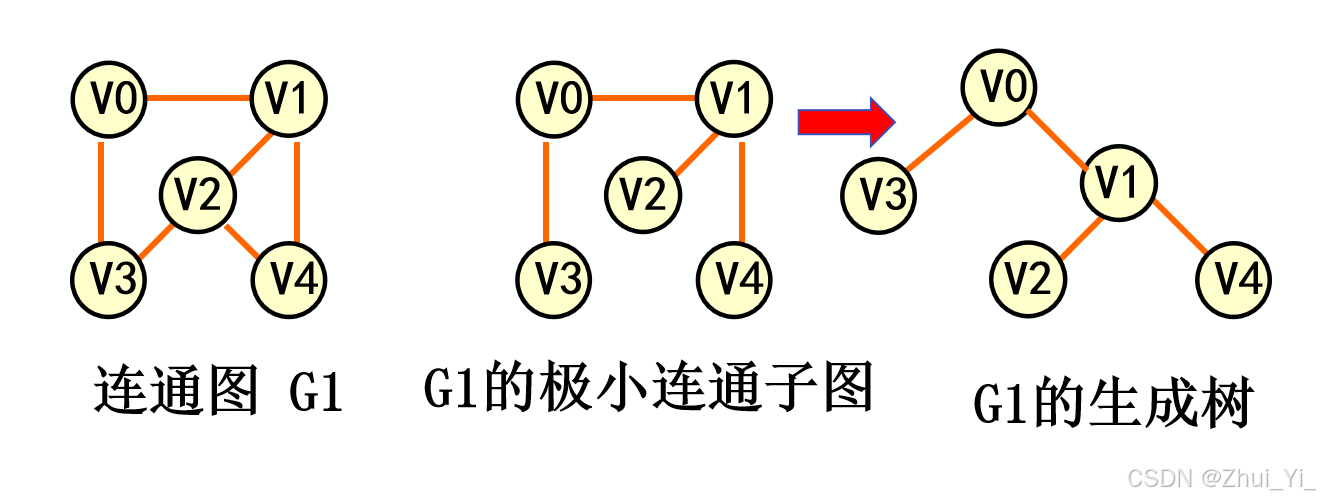
广度优先生成树和深度优先生成树
那么我们上篇文章提到了广度优先遍历和深度优先遍历:
在广度优先遍历和深度优先遍历过程中,可以得到一颗遍历树,我们称之为广度优先生成树和深度优先生成树。
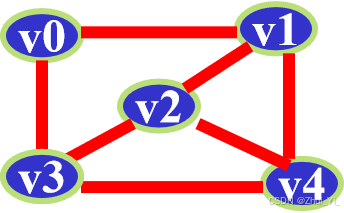
那么我们根据这个图,以v0作为起点,画出生成树。
我们先把邻接表给画出来:

那么画出来深度优先生成树如下:

广度优先生成树如下:

求最小生成树
我们首先明确一下:
那么我们该如何求最小生成树?
构造最小生成树的准则:
那么最小生成树有什么用途呢?

如何求最小生成树
在这里有两种求法:
他们的特点是:
prim算法
基本思想:归并顶点
应用构造最小生成树的过程

我们先把a结点放在u里面,再把其他节点放在v-u里面

然后再找与a相连权值最小的,ab,ac,ad,ae,谁权值最小?ab,再把b放在u里面

然后再找与u里面的结点相连权值最小的:ac,ad,ae,bc,谁权值最小?
bc,再把c放在u里面

然后再找最小的,ad,ae,cd,ce,谁最小?
ad,把d放在u里面
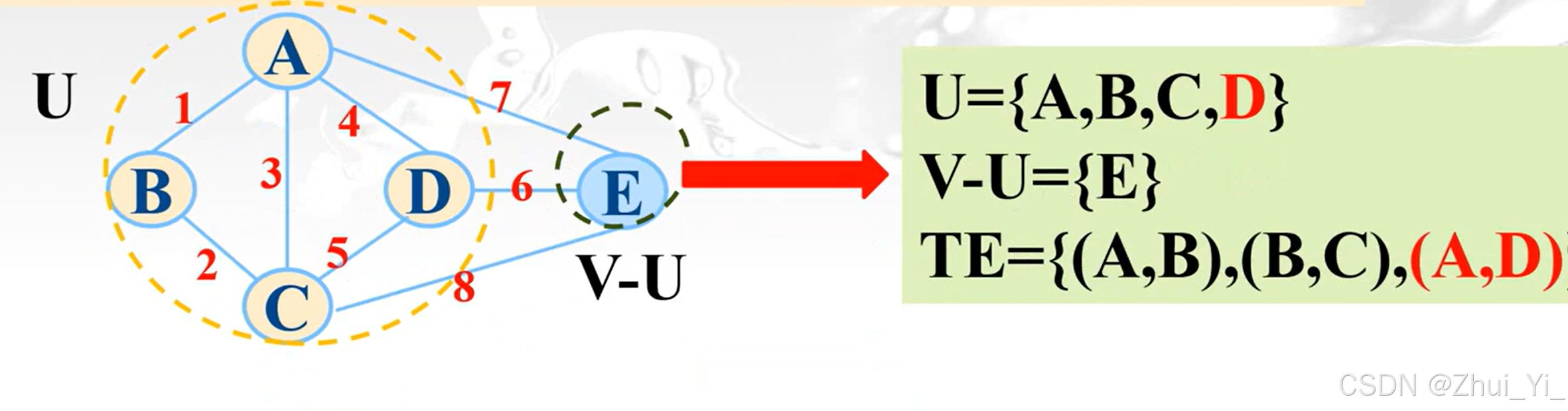
最后就是de

接下来我们考虑几个问题:
如果ae=de=6,我们该选择那条边呢?
都可以,那么从这里我们得到了什么?
最小生成树的形态不唯一。
那么什么是唯一的呢?
最小生成树的权值之和!!!
如何区分点在u还是在v-u集合?
标志变量!!!
这里我们试一下:

画出最小生成树:
先建立邻接矩阵

我们在建立一个一维数组

其中最开始的时候u中只有0,故:
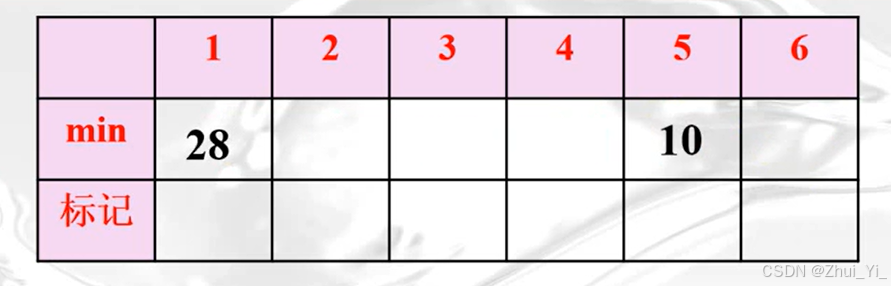
然后再比较谁最小,5,故:
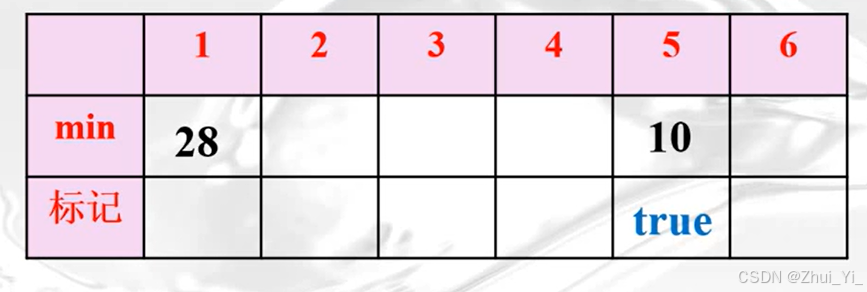
此时u中有0和5,故:

不断重复以上操作:
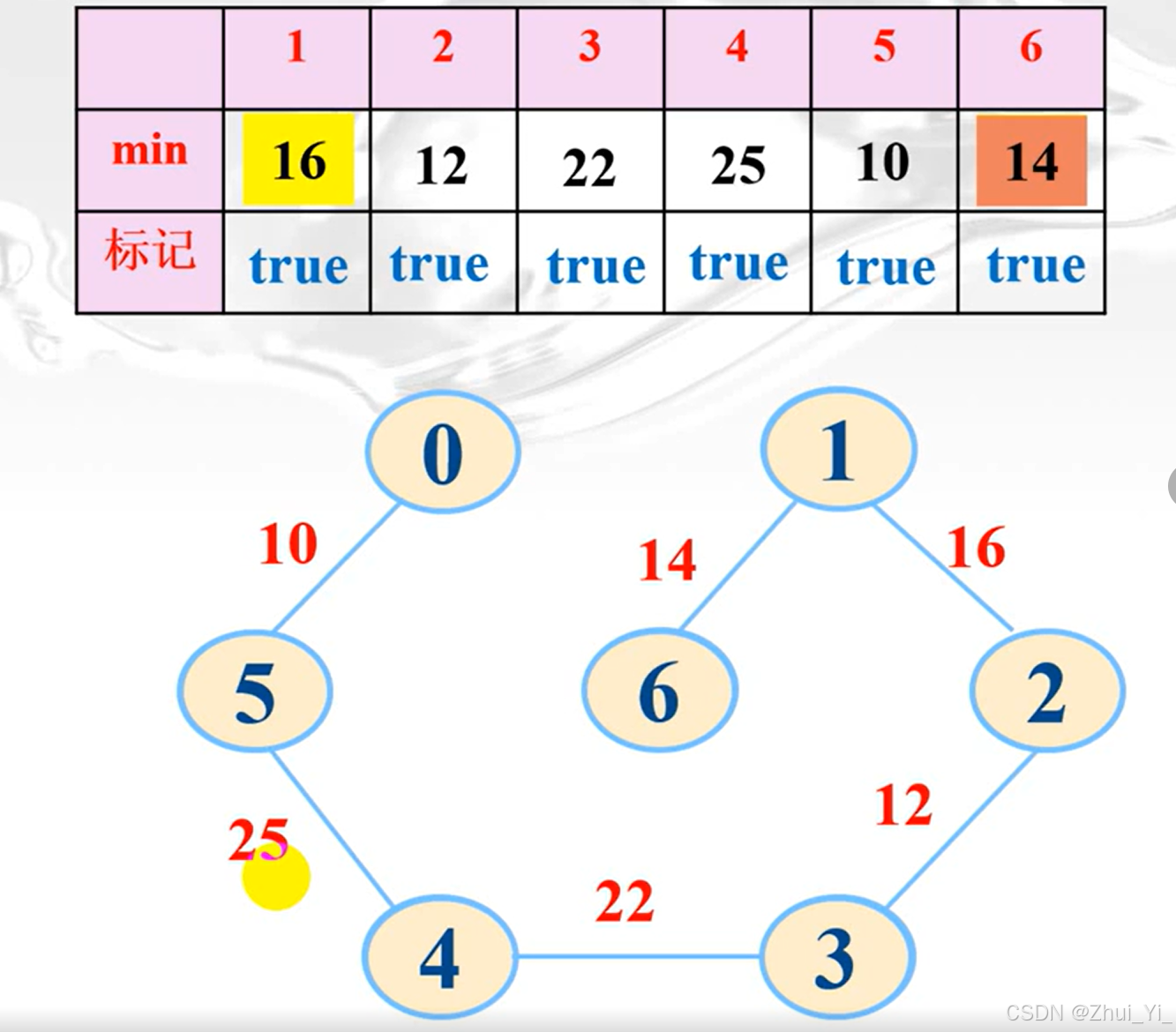
kruscal算法
克鲁斯卡尔算法的基本思想-归并边
- 构造一个只有 n 个顶点,没有边的非连通图 te= { v, }, 每个顶点自成一个连通分量
- 在 e 中选最小权值的边,若该边的两个顶点落在不同的连通分量上,则加入 te 中;否则舍去,重新选择
- 重复下去,直到所有顶点在同一连通分量上为止
实现该算法的关键为如何避免选取的边构成回路

构造上述的最小生成树:
首先按权值大小分:

然后再设置辅助元素的值:

首先选择权值最小的ab,a和b能连嘛?
a的值为0,b的值为1,不一样,可以选,同时使两个顶点的值相同:

然后在选取权值最小的,bc,能选吗?
值不相同,可以,再改变c的值使他们相等:

然后再看谁权值最小,ac,能选吗?
不能,a和c的值都为0。再往下看:
ad,能选吗?
值不相同,能选,再改值:

重复上述操作:

二、最短路径
特别注意,最短路径跟最小生成树是不一样的。最短路径上不一定包含n个顶点。
dijkstra算法
dijkstra算法的思想–按路径长度递增次序求解:

如图。

然后建立表格

存储结构(顶点个数为n)
初始化结果如图

算法思想
如图

这是我给出一个例子:

算法流程图如下:

代码实现如下:
void shortestpath_dij(amgraph g, int v0){
//用dijkstra算法求有向网g的v0顶点到其余顶点的最短路径
n=g.vexnum; //n为g中顶点的个数
for(v = 0; v<n; ++v){ //n个顶点依次初始化
s[v] = false; //s初始为空集
d[v] = g.arcs[v0][v]; //将v0到各个终点的最短路径长度初始化
if(d[v]< maxint) path [v]=v0; //v0和v之间有弧,将v的前驱置为v0
else path [v]=-1; //如果v0和v之间无弧,则将v的前驱置为-1
}//for
s[v0]=true; //将v0加入s
d[v0]=0; //源点到源点的距离为0
/*―开始主循环,每次求得v0到某个顶点v的最短路径,将v加到s集―*/
for(i=1;i<n; ++i){ //对其余n−1个顶点,依次进行计算
min= maxint;
for(w=0;w<n; ++w)
if(!s[w]&&d[w]<min)
{v=w; min=d[w];} //选择一条当前的最短路径,终点为v
s[v]=true; //将v加入s
for(w=0;w<n; ++w) //更新从v0出发到集合v−s上所有顶点的最短路径长度
if(!s[w]&&(d[v]+g.arcs[v][w]<d[w])){
d[w]=d[v]+g.arcs[v][w]; //更新d[w]
path [w]=v; //更改w的前驱为v
}//if
}//for
}//shortestpath_dij
时间复杂度为:o(n2)
三、拓扑排序
引入
比如教学计划的制定
哪些课程是必须先修的,哪些课程是可以并行学习的。
aov网

如图。
aoe网

如图。
aov网示例

如图
应该这样画。
算法思想(重复选择没有直接前驱的顶点)
总结
本篇文章有点粗造,抱歉各位,状态不是很好。
希望可以三哈!!!





发表评论