bfs 算法简介
bfs是广度优先搜索(breadth-first search)的缩写,是一种图遍历算法。它从给定的起始节点开始,逐层地向外扩展,先访问起始节点的相邻节点,然后再访问相邻节点的相邻节点,以此类推,直到遍历完所有可达节点。
具体的bfs算法流程如下:
- 创建一个队列,并将起始节点入队;
- 将起始节点标记为已访问;
- 当队列不为空时,循环执行以下操作: a. 出队一个节点; b. 访问该节点; c. 将该节点的所有未访问相邻节点入队,并标记为已访问;
- 遍历完成。
bfs算法的特点是按照层级进行遍历,先访问离起始节点最近的节点,再访问离起始节点稍远一层的节点,依次类推。由于bfs需要使用队列来辅助实现,因此可以保证每个节点被访问且仅被访问一次。
bfs算法广泛应用于图的遍历、最短路径、连通性检测等问题,也可以用于解决一些搜索问题,例如在迷宫中找到最短路径等。
经典 bfs 问题
n叉树的层序遍历
n 叉树的层序遍历

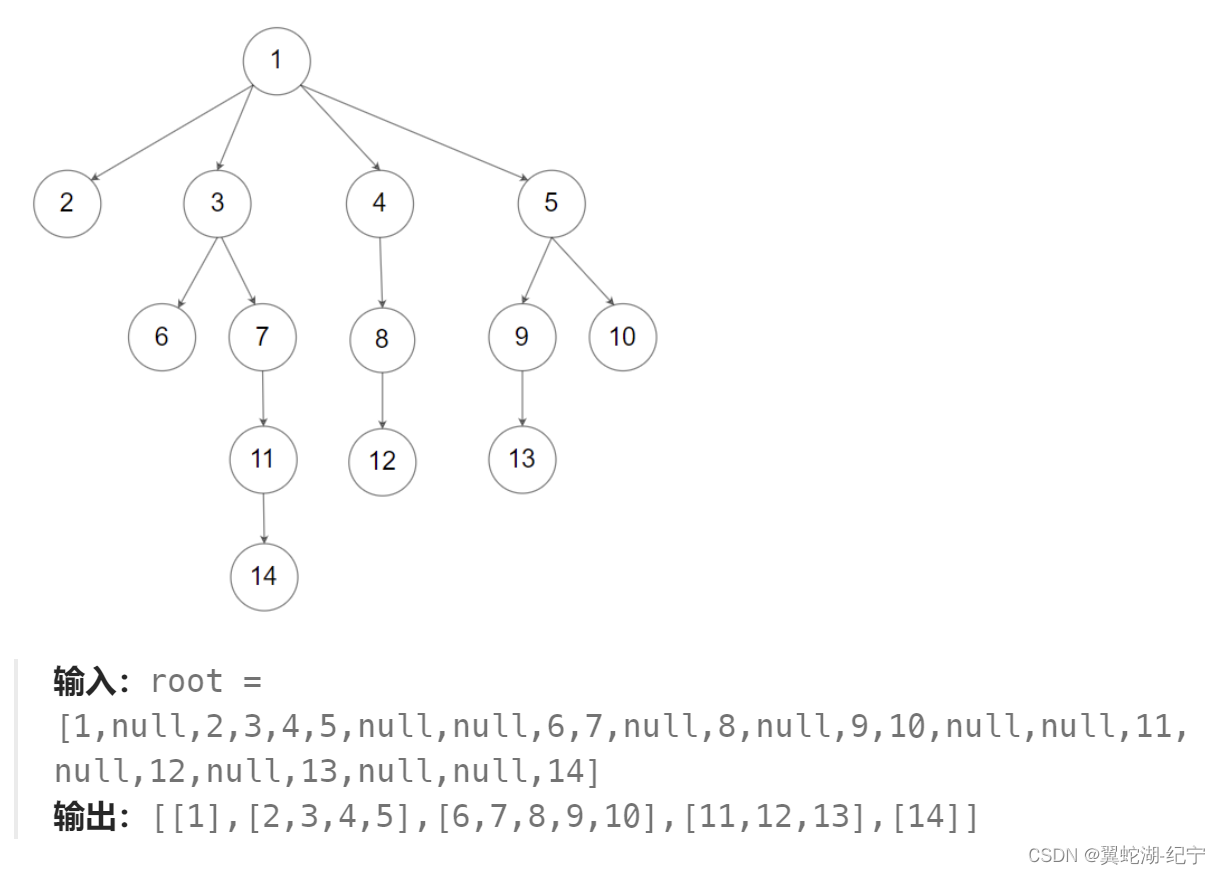
这就是一个典型的层序遍历问题,将一层的节点入队列后,记录这一层的个数 sz,每当有个节点出队列一次,就将他的所有孩子节点都入队列,如此往复…
力扣代码:
/*
// definition for a node.
class node {
public:
int val;
vector<node*> children;
node() {}
node(int _val) {
val = _val;
}
node(int _val, vector<node*> _children) {
val = _val;
children = _children;
}
};
*/
class solution {
public:
vector<vector<int>> levelorder(node* root) {
vector<vector<int>> ret;
queue<node*> q;
if(root == nullptr) return ret;
q.push(root);
while(!q.empty())
{
int sz = q.size();
vector<int> tmp;
for(int i = 0; i < sz; i++)
{
node* t = q.front();
tmp.push_back(t->val);
q.pop();
for(auto &e: t->children)
{
if(e!=nullptr) q.push(e);
}
}
ret.push_back(tmp);
}
return ret;
}
};
bfs 解决最短路问题
这里的最短路问题,指的是边权相同的最短路问题。

如图,从 a 开始,走到 i 的最短路径是多少?
步骤:从起点开始,每一步都可能会有多种选择,每走一步,将下一次的所有选择都 “同时” 入队列(保证他们向外扩展的速度相同),同时将每一步得的位置都存入哈希表中,当准备入队时,发现哈希表中已经存在当前位置了,就不入队(因为时同时向外扩展得,所以当此位置已经在哈希表中存在时,说明当前这条路一定不是最佳选择,则舍去),记录公同向外扩展的次数,就是最短的路径长度!
迷宫中离入口最近的出口

这道题是经典的最短路径问题,也就是我们说的模板题
class solution {
public:
int dx[4] = {0, 0, 1, -1};
int dy[4] = {1, -1, 0, 0};
int nearestexit(vector<vector<char>>& maze, vector<int>& entrance) {
int m = maze.size(), n = maze[0].size();
bool vis[m][n];
memset(vis, 0, sizeof vis);
queue<pair<int, int>> q;
q.push({entrance[0], entrance[1]});
vis[entrance[0]][entrance[1]] = true;
int step = 0; // 记录路径长度
while(q.size() > 0)
{
step ++;
int sz = q.size();
for(int i = 0; i < sz; i++)
{
auto [a, b] = q.front();
q.pop(); // 取出队头元素并出队
for(int j = 0; j < 4; j++)
{
// 找出队头元素的多种道路选择
int x = a + dx[j];
int y = b + dy[j];
if(x >= 0 && x < m && y >= 0 && y < n && maze[x][y] == '.' && !vis[x][y])
{
if(x == 0 || x == m - 1 || y == 0 || y == n - 1) return step;
q.push({x, y}); // 将这种道路选择入队
vis[x][y] = true;
}
}
}
}
return -1;
}
};
多源bfs最短路问题
多源bfs最短路问题是一个经典的图论问题,也被称为全源最短路径问题。给定一个带权有向图和图中的多个源点,要求计算出从每个源点到图中所有其他节点的最短路径。
如果将多个源点的 bfs 问题,转化为多个单源点的 bfs 问题,但是大概率会超时,时间复杂度过高。
那么怎么办呢?将多个节点看作一个超级源点,将他们同时入队即可,然后一层一层的往外扩展,在写代码上,只需要将单源最短路中的将起点入队,改为将题目中给出的所有节点入队即可!
01 矩阵
01 矩阵
给定一个由 0 和 1 组成的矩阵 mat ,请输出一个大小相同的矩阵,其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。
两个相邻元素间的距离为 1 。

这是一个经典的多源 bfs 问题
但如果将1当作起点,0 当作终点的话,很难判定它的距离,于是我们正难则反,将0当作起点(将所有的 0 入队),1 当作终点进行一个多源 bfs 即可!
class solution
{
int dx[4] = { 0, 0, 1, -1 };
int dy[4] = { 1, -1, 0, 0 };
public:
vector<vector<int>> updatematrix(vector<vector<int>>& mat)
{
int m = mat.size(), n = mat[0].size();
// dist[i][j] == -1 表⽰:没有搜索过
// dist[i][j] != -1 表⽰:最短距离
vector<vector<int>> dist(m, vector<int>(n, -1));
queue<pair<int, int>> q;
// 1. 把所有的源点加⼊到队列中
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
if (mat[i][j] == 0)
{
q.push({ i, j });
dist[i][j] = 0;
}
// 2. ⼀层⼀层的往外扩
while (q.size())
{
auto [a, b] = q.front(); q.pop();
for (int i = 0; i < 4; i++)
{
int x = a + dx[i], y = b + dy[i];
if (x >= 0 && x < m && y >= 0 && y < n && dist[x][y] == -1)
{
dist[x][y] = dist[a][b] + 1;
q.push({ x, y });
}
}
}
return dist;
}
};




发表评论