文章目录
1.题目
2.例子
number=4,capacity=8
| 物品编号(i) | w(体积) | v(价值) |
|---|---|---|
| 1 | 2 | 3 |
| 2 | 3 | 4 |
| 3 | 4 | 5 |
| 4 | 5 | 6 |
3.实现
1.动态规划
1.什么是动态规划
2.对题目分析
1.分析
2.状态转换方程
if(j>=w[i])
m[i][j]=max(m[i-1][j],m[i-1][j-weight[i]]+value[i]);
else
m[i][j]=m[i-1][j];
3.状态转换图
3.代码
#define n 100
#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
void knap(int value[], int weight[], int c, int n, int m[][n])
{
for (int i = 1; i <= n; i++)//物品i
{
for (int j = 1; j <= c; j++)//重量j
{
if (j >= weight[i])
{
m[i][j] = max(m[i - 1][j], m[i - 1][j - weight[i]] + value[i]);
}
else m[i][j] = m[i - 1][j];
}
}
//for (int i = 0; i <= n; i++)//物品i
//{
// for (int j = 0; j <= c; j++)//重量j
// {
// cout << m[i][j] << ' ';
// }
// cout << endl;
//}
}
void trace(int m[][n], int weight[], int c, int n, int x[])
{
int h = n, g = c;
while (h >= 1)
{
if (m[h][g] == m[h - 1][g])
x[h] = 0;
else
{
x[h] = 1;
g = g - weight[h];
}
h--;
}
}
int main()
{
int value[100];
int weight[100];
int m[n][n] = { 0 };
int x[n];
int c;
int n;
value[0] = 0;
weight[0] = 0;
cout << "请输入背包可以承受的重量:";
cin >> c;
cout << "请输入物体数量:";
cin >> n;
for (int i = 1; i <= n; i++)
{
printf("请输入第%d个物体的质量与价值:", i);
cin >> weight[i] >> value[i];
}
knap(value, weight, c, n, m);
trace(m, weight, c, n, x);
for (int i = 1; i <= n; i++)
cout << x[i] << " ";
cout << endl;
return 0;
}
4.结果

2.贪心算法
1.什么是贪心算法
2.对题目分析
1.分析
2.缺点
3.代码
#include <iostream>
#include<algorithm>
using namespace std;
struct node
{
double v;//价值
double w;//重量
} wu[100];
bool cmp1(node a, node b)//重量
{
if (a.w == b.w)
return a.v > b.v;
return a.w < b.w;
}
bool cmp2(node a, node b)//价值
{
if (a.v == b.v)
return a.w < b.w;
return a.v > b.v;
}
bool cmp3(node a, node b)// 单位价值
{
if ((a.v / a.w) == (b.v / b.w))
return a.w < b.w;
return (a.v / a.w) > (b.v / b.w);
}
int fun1(int n, int c)
{
sort(wu, wu + n, cmp1);
int value = 0;
for (int i = 0; i < n; i++)
{
if (c >= wu[i].w)
{
c -= wu[i].w;
value += wu[i].v;
}
}
return value;
}
int fun2(int n, int c)
{
sort(wu, wu + n, cmp2);
int value = 0;
for (int i = 0; i < n; i++)
{
if (c >= wu[i].w)
{
c -= wu[i].w;
value += wu[i].v;
}
}
return value;
}
int fun3(int n, int c)
{
sort(wu, wu + n, cmp3);
int value = 0;
for (int i = 0; i < n; i++)
{
if (c >= wu[i].w)
{
c -= wu[i].w;
value += wu[i].v;
}
}
return value;
}
int random(int n, int c)
{
int ans = -1, m = 1000;
int flag, b[110];
while (m--)
{
int flag2 = 0, value = 0;
for (int i = 0; i < n; i++)
{
b[i] = 1;
}
while (1)
{
flag = rand() % n;
if (b[flag] != 0)
{
if (flag2 + wu[flag].w <= c)
{
flag2 += wu[flag].w;
b[flag] = 0;
value += wu[flag].v;
}
}
else
{
break;
}
}
if (value > ans)
{
ans = value;
}
}
return ans;
}
int main()
{
int n, c;//n个物品,c的容量
cin >> n >> c;
for (int i = 0; i < n; i++)
cin >> wu[i].w;
for (int j = 0; j < n; j++)
cin >> wu[j].v;
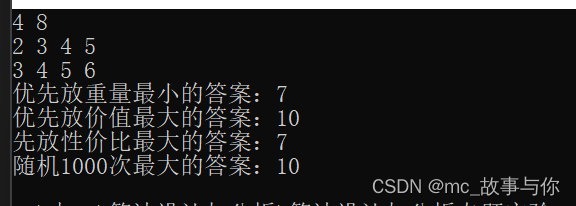
cout << "优先放重量最小的答案:";
cout << fun1(n, c) << endl;
cout << "优先放价值最大的答案:";
cout << fun2(n, c) << endl;
cout << "先放性价比最大的答案:";
cout << fun3(n, c) << endl;
cout << "随机1000次最大的答案:";
cout << random(n, c) << endl;
return 0;
}
4.结果
3.回溯法
1.什么是回溯法
2.对题目分析
1.分析
2.设计
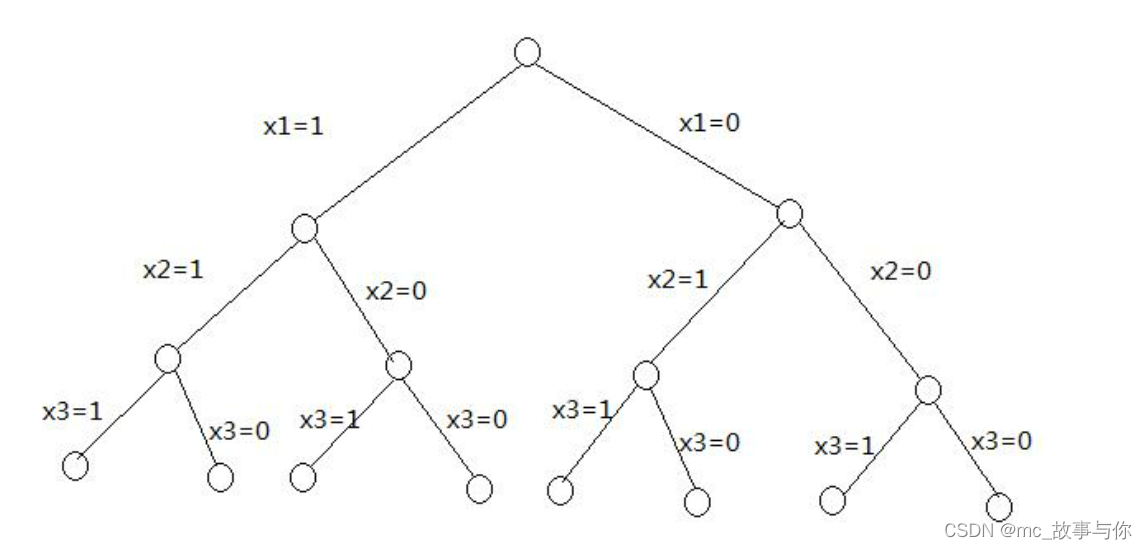
3.解空间树图
4.时间复杂度与空间复杂度
3.代码
#include <iostream>
#include <stdio.h>
//#include <conio.h>
using namespace std;
int n;//物品数量
double c;//背包容量
double v[100];//各个物品的价值
double w[100];//各个物品的重量
double cw = 0.0;//当前背包重量
double cp = 0.0;//当前背包中物品总价值
double bestp = 0.0;//当前最优价值
double perp[100];//单位物品价值(排序后)
int order[100];//物品编号
//按单位价值排序
void knapsack()
{
int i, j;
int temporder = 0;
double temp = 0.0;
for (i = 1; i <= n; i++)
perp[i] = v[i] / w[i]; //计算单位价值(单位重量的物品价值)
for (i = 1; i <= n - 1; i++)
{
for (j = i + 1; j <= n; j++)
if (perp[i] < perp[j])//冒泡排序perp[],order[],sortv[],sortw[]
{
temp = perp[i]; //冒泡对perp[]排序
perp[i] = perp[j];//单位物品价值
perp[j] = temp;
temporder = order[i];//冒泡对order[]排序
order[i] = order[j];;//物品编号
order[j] = temporder;
temp = v[i];//冒泡对v[]排序
v[i] = v[j];//各个物品的价值
v[j] = temp;
temp = w[i];//冒泡对w[]排序
w[i] = w[j];//各个物品的重量
w[j] = temp;
}
}
}
//计算上界函数,功能为剪枝
double bound(int i)
{ //判断当前背包的总价值cp+剩余容量可容纳的最大价值<=当前最优价值
double leftw = c - cw;//剩余背包容量
double b = cp;//记录当前背包的总价值cp,最后求上界
//以物品单位重量价值递减次序装入物品
while (i <= n && w[i] <= leftw)
{
leftw -= w[i];
b += v[i];
i++;
}
//装满背包
if (i <= n)
b += v[i] / w[i] * leftw;
return b;//返回计算出的上界
}
//回溯函数
void backtrack(int i)
{ //i用来指示到达的层数(第几步,从0开始),同时也指示当前选择玩了几个物品
if (i > n) //递归结束的判定条件
{
bestp = cp;
return;
}
//如若左子节点可行,则直接搜索左子树;
//对于右子树,先计算上界函数,以判断是否将其减去
if (cw + w[i] <= c)//将物品i放入背包,搜索左子树
{
cw += w[i];//同步更新当前背包的重量
cp += v[i];//同步更新当前背包的总价值
backtrack(i + 1);//深度搜索进入下一层
cw -= w[i];//回溯复原
cp -= v[i];//回溯复原
}
if (bound(i + 1) > bestp)//如若符合条件则搜索右子树
{
backtrack(i + 1); //后续节点的价值上界大于当前最优价值,则可以进入右界面 否则最优的都小于或等于当前的 就没必要再进入右节点
//进入右节点 因为不加入到背包 故 当前的价值 重量 都不发生改变
}
}
int main()
{
int i;
printf("请输入物品的数量和背包的容量:");
scanf_s("%d %lf", &n, &c);
printf("请依次输入%d个物品的重量:\n", n);
for (i = 1; i <= n; i++)
{
scanf_s("%lf", &w[i]);
order[i] = i;
}
printf("请依次输入%d个物品的价值:\n", n);
for (i = 1; i <= n; i++)
{
scanf_s("%lf", &v[i]);
}
knapsack();
backtrack(1);
cout << endl;
printf("最优价值为:%.lf\n", bestp);
return 0;
}
4.结果

4.分支限界法
1.什么是分支限界法
2.对题目分析
1.分析
2.时间复杂度与空间复杂度
3.代码方法1
#include <iostream>
#include<cstdio>
#include<queue>
using namespace std;
const int n = 110;
struct stone {
int v, w;
stone() {
v = w = 0;
}
bool operator < (stone b) const {
return v / w > b.v / b.w;
}
}item[n];
struct node {
int level, cv, cw;
float bound;
bool operator< (const node& b) const {
return bound > b.bound;
}
};
int best, w, n;
inline void initialize(priority_queue<node>& q) {
while (q.size()) q.pop();
}
float bound(node& p) {
int left = w - p.cw;
float val = p.cv;
int i;
for (i = p.level; i <= n && item[i].w <= left; i++) {
left -= item[i].w;
val += item[i].v;
}
if (i <= n) val += item[i].v * 1.0 / item[i].w * left;
return val;
}
priority_queue<node> pq;
void knapsack() {
node u, v;
initialize(pq);
v = { 0,0,0,0 };
best = 0;
v.bound = bound(v);
pq.push(v);
while (pq.size()) {
v = pq.top();
pq.pop();
if (v.level == n) continue;
if (v.bound > best) {
u.level = v.level + 1;
u.cw = v.cw + item[u.level].w;
u.cv = v.cv + item[u.level].v;
//printf("%d %d\n", u.cw, u.cv);
if (u.cw <= w && u.cv > best)
best = u.cv;
u.bound = bound(u);
if (u.bound > best) pq.push(u);
u.cw = v.cw; u.cv = v.cv;
u.level = v.level + 1;
u.bound = bound(u);
if (u.bound > best) pq.push(u);
}
}
}
int main() {
printf("请输入物品的数量和背包的容量:");
scanf_s("%d %d", &n, &w);
printf("请依次输入%d个物品的重量:\n", n);
for (int i = 1; i <= n; i++)
{
scanf_s("%d", &item[i].w);
}
printf("请依次输入%d个物品的价值:\n", n);
for (int i = 1; i <= n; i++)
{
scanf_s("%d", &item[i].v);
}
sort(item + 1, item + 1 + n);
knapsack();
printf("%d\n", best);
return 0;
}
/*
4 7
3 5 2 1
9 10 7 4
20
*/
4.结果1

5.代码方法2
#include <iostream>
#include<cstdio>
#include<queue>
using namespace std;
//分支限界发求解01背包问题 基于的是贪心思想 在第1个物品放入 和没放入背包时 其实 都有一个理论上可能达到的最大价值
//我们选理论价值最大的那个可能性 如果该物品放入背包 可能的价值大 我们就走这条路 如果这个不放入 价值大 我们就走另外一条路
//总容量
int totalvolume;
//物品数量
int amount;
//递增系数
int id_add = 0;
//定义一个结构
struct element
{
//编号
int id;
//重量
int weight;
// 价值
int worth;
element()
{
id = id_add++;
weight = 0;
worth = 0;
}
};
//保存某个方案
struct plan
{
//每个方案都会保存一个数组 (每个物品 是否放入)
bool isin[11] = { 0 };
// 已经存入的物品的价值
double alreadyworth;
//可能最大利益
double mostworth;
//剩余容量
int leftvolume;
//第id个物品是否放入 这表示前id-1个物品 是否放入都已经确定了
int id;
plan()
{
}
//初始化 所有物品都没放入的初始状态
void init(element* array)
{
alreadyworth = 0;
mostworth = 0;
leftvolume = totalvolume;
id = 0;
calculate(array);
};
//后序所有的初始化都采用这个 都是在前面基础上 判断第n个物品是否放入 放入是1 不放入是0
void init(plan& a, int is_in, element* array)
{
std::copy(a.isin, a.isin + amount, isin);
//不放入
id = a.id;
leftvolume = a.leftvolume;
alreadyworth = a.alreadyworth;
//放入
if (is_in == 1 && leftvolume - array[id].weight >= 0)
{
leftvolume -= array[id].weight;
alreadyworth += array[id].worth;
isin[id] = 1;
}
id++;
calculate(array);
};
//计算某个方案的 mostworth
void calculate(element* array)
{
int id_used = id;
int leftvolume1 = leftvolume;
mostworth = alreadyworth;
while (id_used <= amount - 1 && leftvolume1 - array[id_used].weight >= 0)
{
leftvolume1 -= array[id_used].weight;
mostworth += array[id_used].worth;
id_used++;
}
if (leftvolume1 > 0 && id_used <= amount - 1)
{
mostworth += leftvolume1 * ((double)array[id_used].worth / (double)array[id_used].weight);
}
}
};
bool operator<(const plan& a, const plan& b)
{
return a.mostworth < b.mostworth;
}
bool operator>(const plan& a, const plan& b)
{
return a.mostworth > b.mostworth;
}
bool operator>=(const plan& a, const plan& b)
{
return a.mostworth >= b.mostworth;
}
ostream& operator<<(ostream& os, const plan& a)
{
for (int i = 0; i <= 10; i++)
{
if (a.isin[i] == 1)
{
os << i + 1 << " ";
}
}
os << "最优方案价值为" << a.alreadyworth << endl;
return os;
}
bool cmp_element(element& a, element& b)
{
return ((double)a.worth / a.weight) > ((double)b.worth / b.weight);
}
int main()
{
srand((unsigned)time(null));
//大根堆
priority_queue<plan>mheap;
cout << "请输入总的容量" << endl;
cin >> totalvolume;
cout << "输入物品数量" << endl;
cin >> amount;
element* item = new element[amount];
for (int i = 0; i < amount; i++)
{
cout << "输入第" << i + 1 << "组物品的重量和价值。以空格隔开" << endl;
cin >> item[i].weight >> item[i].worth;
}
//按性价比排序
std::sort(item, item + amount, cmp_element);
cout << " 排序之后:" << endl;
for (int i = 0; i < amount; i++)
{
cout << i + 1 << " " << item[i].weight << " " << item[i].worth << endl;
}
//临时方案
plan tempplan;
tempplan.init(item);
//临时方案
plan tempplan1;
while (tempplan.id != amount)
{
//第n个物品放入
tempplan1.init(tempplan, 0, item);
mheap.push(tempplan1);
//第n个物品不放入
tempplan1.init(tempplan, 1, item);
mheap.push(tempplan1);
tempplan = mheap.top();
mheap.pop();
}
//循环结束的方案 即为最优方案 因为到达叶子节点
cout << tempplan;
system("pause");
delete[]item;
return 0;
}
6.结果2





发表评论