什么是批次效应
批次效应(batch effect)是实验或研究中经常遇到的一种现象,它指的是在数据采集过程中由于各种因素导致的系统性变异,而且它与我们研究的变量没有半毛钱关系!
一般批次效应可能来自:
- 实验的不同部分在不同时间完成
- 实验的不同部分由不同的实验者完成
- 实验条件的变化,如实验仪器、试剂批次、试剂用量、测序批次等等
- 数据来源不同,如将自己的数据集与公共数据集整合分析
- ……
比如在生物学研究中,常常需要通过高通量技术同时测量多个生物学特征。这些数据通常大规模生成,会涉及多个实验批次和操作者,这就很容易产生批次效应。
批次效应的存在可能对数据分析和解释产生负面影响,因此我们在进行分析时,特别是在高通量实验中,及时鉴定和处理批次效应是非常重要的!
批次效应的影响
批次效应可能对实验结果产生多方面的影响,其中一些主要的影响包括:
- 引入系统性误差: 批次效应可能引入实验中的系统性误差,使得测量结果在不同批次之间产生偏差。这会导致对研究变量的准确性评估受到干扰。
- 降低实验的可重复性: 如果批次效应未得到妥善处理,不同实验批次之间的一致性可能降低,从而影响实验的可重复性和结果的稳定性。
- 混淆生物学差异: 批次效应可能掩盖或混淆真实的生物学差异,使得研究人员难以区分实验条件引起的变异和研究变量本身的差异。
- 影响数据解释: 未考虑批次效应可能导致对实验结果的错误解释。在解释数据时,研究人员可能错误地将批次效应归因于研究变量,从而得出误导性的结论。
- 影响实验设计的有效性: 批次效应的存在可能影响实验设计的有效性,尤其是在高通量实验中。合理设计实验以考虑和控制批次效应是确保实验结果可靠性的重要步骤。
为了应对批次效应,我们可以采取一系列措施,比如使用统计方法进行批次校正、随机化实验条件、控制实验条件的一致性等,以最大程度地减少批次效应对实验结果的影响,以提高结果的可靠性和可重复性。
今天我们主要介绍如何进行批次校正!
如何鉴定数据存在批次效应
那我们该如何判断整合后的数据是否存在批次效应呢?
鉴定数据中是否存在批次效应是确保实验结果可靠性的关键步骤之一。以下是一些常用的方法和技巧,用于检测和鉴定数据中的批次效应:
- 可视化分析: 我们可以将批次效应进行可视化,通过各种图表比如散点图、箱线图、聚类热图等,观察不同批次或实验条件下数据的分布情况。如果存在批次效应,不同批次的数据就可能会显示出明显的差异。
- 统计分析: 利用统计方法来检测批次效应。常用的方法包括方差分析(anova)、线性混合效应模型(mixed effects models)、主成分分析(pca)等。这些方法可以帮助确定批次效应是否显著,并提供量化的结果。
我们边实战边介绍!
数据准备
首先我们要了解自己的数据,比如判定它的数据类型、是否为标准化数据等。毕竟,知己知彼,才能百战百胜嘛!
今天我们使用的数据是在geo数据库下载的,我找了三个不同的数据集(gse58812、gse167213、gse120196),都是表达芯片数据,而且用的是同一个芯片!
我还要专门提一嘴,为什么我要找三个数据集(两个三阴性乳腺癌数据集和一个卵巢癌数据集)嘞!人家不一般都用两个数据集举例嘛!哎嘿!且听我细细道来!
这是因为呐,在去除批次效应的过程中,存在一定的风险,可能会误伤原本存在的样本差异。这是因为批次效应校正的方法通常是基于样本之间的共变异性,而这个共变异性中既包含了批次效应,也可能包含了其他来源的变异,包括样本类型之间的差异。比如我们的样本中有肿瘤和正常两种类型,二者本来就有差别,我们不能矫枉过正对不对!所以呀,我们在去除批次效应时,一定要谨慎选择校正方法,以确保不会将真实的生物学差异误判为批次效应。
################################# geo数据下载 ##################################
# 数据下载,这部分有点多,我就不详细介绍啦!
# 大家也可以跳过这部分!直接去github下载现成的数据进行批次处理的学习哟!
library(geoquery)
# gse58812数据集的下载与处理(dataset1-tnbc)
gse_number = "gse58812"
# 这一步啊,看运气!网络时好时坏,是个玄学!一次不行不要慌!咱多跑几次!总会成功的!
geo_data <- getgeo(gse_number, destdir = './batch_effect_data/', getgpl = f)
geo_data <- geo_data[[1]]
# 提取表达矩阵
exp <- exprs(geo_data)
dim(exp)
# [1] 54675 107
exp[1:4, 1:4]
# gsm1419942 gsm1419943 gsm1419944 gsm1419945
# 1007_s_at 3958.0740 7621.8810 2317.2720 2418.0670
# 1053_at 456.1156 417.4807 433.5571 718.3322
# 117_at 273.0780 236.7307 457.9662 488.8945
# 121_at 438.8252 283.6443 319.7552 332.9471
# 如果表达矩阵为空,大概率是转录组数据,不能用这个流程,咱们后面会讲的哈!
# 大家自行判断是否需要log
exp <- log2(exp + 1)
# gse167213数据集的下载与处理(dataset2-tnbc)
gse_number = "gse167213"
# 这一步啊,看运气!网络时好时坏,是个玄学!一次不行不要慌!咱多跑几次!总会成功的!
geo_data <- getgeo(gse_number, destdir = './batch_effect_data/', getgpl = f)
geo_data <- geo_data[[1]]
# 提取表达矩阵
exp2 <- exprs(geo_data)
dim(exp2)
# [1] 54675 124
exp2[1:4, 1:4]
# gsm5099604 gsm5099605 gsm5099606 gsm5099607
# 1007_s_at 9.836616 8.988008 9.277235 9.089174
# 1053_at 3.435473 4.067368 3.378283 3.620637
# 117_at 5.139052 6.093664 5.184964 5.679944
# 121_at 7.912213 7.586190 7.344398 7.532436
# 这个就不log啦!
# gse120196数据集的下载与处理(dataset3-ov)
gse_number = "gse120196"
# 这一步啊,看运气!网络时好时坏,是个玄学!一次不行不要慌!咱多跑几次!总会成功的!
geo_data <- getgeo(gse_number, destdir = './batch_effect_data/', getgpl = f)
geo_data <- geo_data[[1]]
# 提取表达矩阵
exp3 <- exprs(geo_data)
# exp3 <- exp3[, -c(1:4)]
dim(exp3)
# [1] 54675 14
exp3[1:4, 1:4]
# gsm3395860 gsm3395861 gsm3395862 gsm3395863
# 1007_s_at 8.395595 8.476796 8.120195 8.370790
# 1053_at 4.507920 4.501397 4.532270 4.601850
# 117_at 5.268016 5.420156 7.006041 6.100746
# 121_at 8.080111 8.540524 8.172471 8.570966
# 这个也不log啦!
# 接下来我们进行数据集合并
# 为了方便区分数据来源,我们先给它把列名改一下!
colnames(exp) <- paste0("dataset1-tnbc", 1:107)
colnames(exp2) <- paste0("dataset2-tnbc", 1:124)
colnames(exp3) <- paste0("dataset3-ov", 1:14)
# 合并数据集
# 现在样本量有点大,可能会运行比较慢,所以为了方便演示和提升大家复现的效率
# 我们每个数据集取十个样本好不好!
exp_all <- cbind(exp[, 1:10], exp2[, 1:10], exp3[, 1:10])
dim(exp_all)
# [1] 54675 30
exp_all[1:4, 1:4]
# dataset1-tnbc1 dataset1-tnbc2 dataset1-tnbc3 dataset1-tnbc4
# 1007_s_at 11.950947 12.896121 11.178834 11.240235
# 1053_at 8.836415 8.709017 8.763402 9.490514
# 117_at 8.098443 7.893184 8.842244 8.936327
# 121_at 8.780786 8.153016 8.325329 8.383476
# 现在我们的三个数据集就合并完毕啦!
# 保存一下
saverds(exp_all, file = "./batch_effect_data/exp_all.rds")
可视化批次效应
让我们用眼睛来看看这三个数据集有没有批次效应!
-
箱线图
最简单粗暴的方法,箱线图!
boxplot(exp_all, las = 2, cex.axis = 0.6)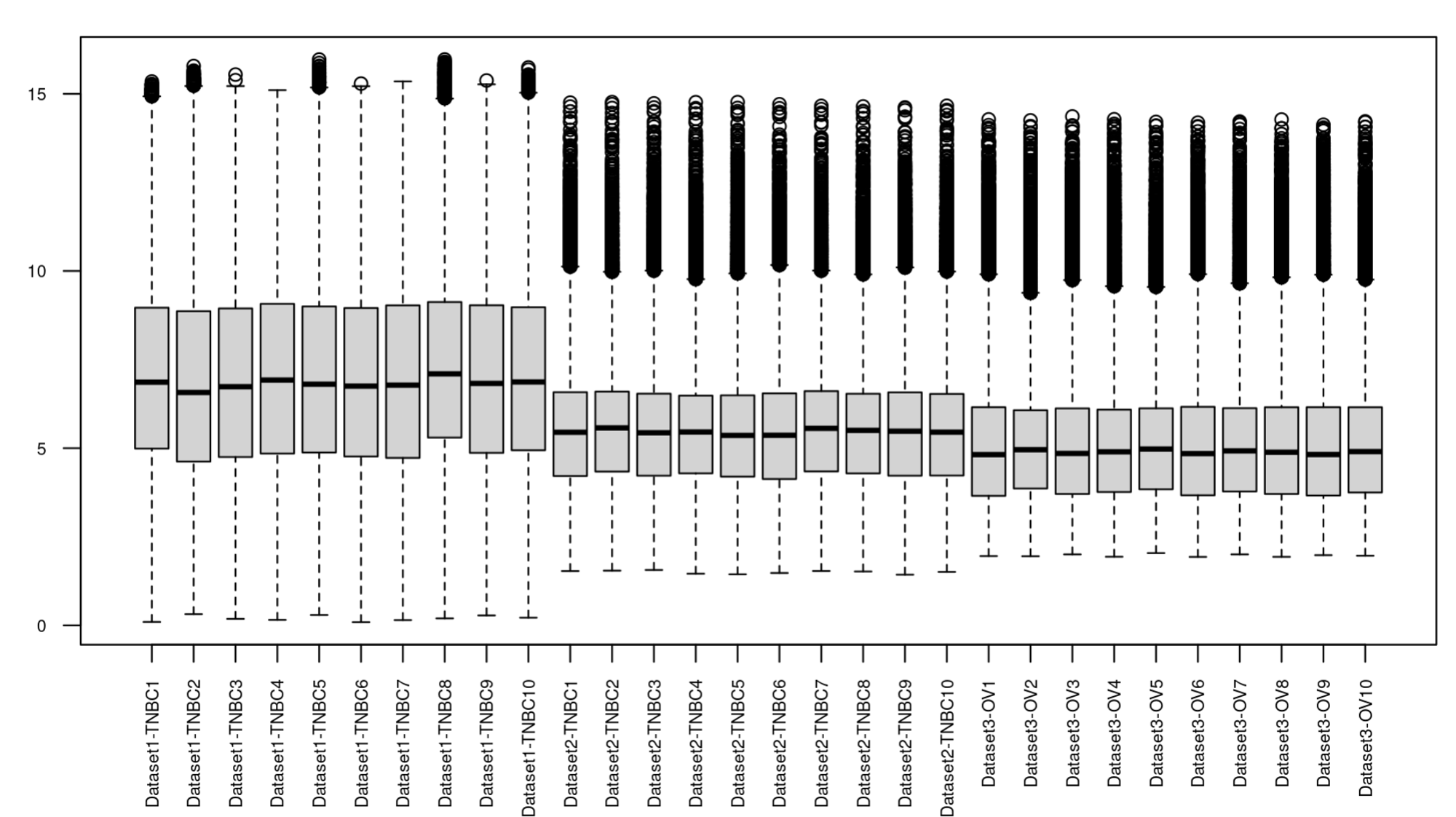
我们可以看到三个数据集存在显著的批次效应。其中,卵巢癌和乳腺癌有显著差异很正常,因为这两种癌症本身就有生物学差异。但我们可以观察到,尽管前两个数据集都是乳腺癌,但不同来源的数据集中的样本之间存在显著差异,这就是所谓的批次效应啦!这种差异就可能会对乳腺癌的生物学差异的解释产生影响,所以我们就需要对其进行批次效应的校正,以确保我们观察到的差异是真实的生物学差异,而非实验过程的影响。
我们可以看到dataset1-tnbc数据集比其他两个数据集的箱子更长哈哈哈哈哈哈,虽然这不是重点!其实一般在去除批次效应之前,我们最好再把合并后的数据先进行标准化处理,这种做法在多数情况下都是有益的!
# 对数据进行简单的标准化 exp_all <- scale(exp_all) # 箱线图2.0 boxplot(exp_all, las = 2, cex.axis = 0.6)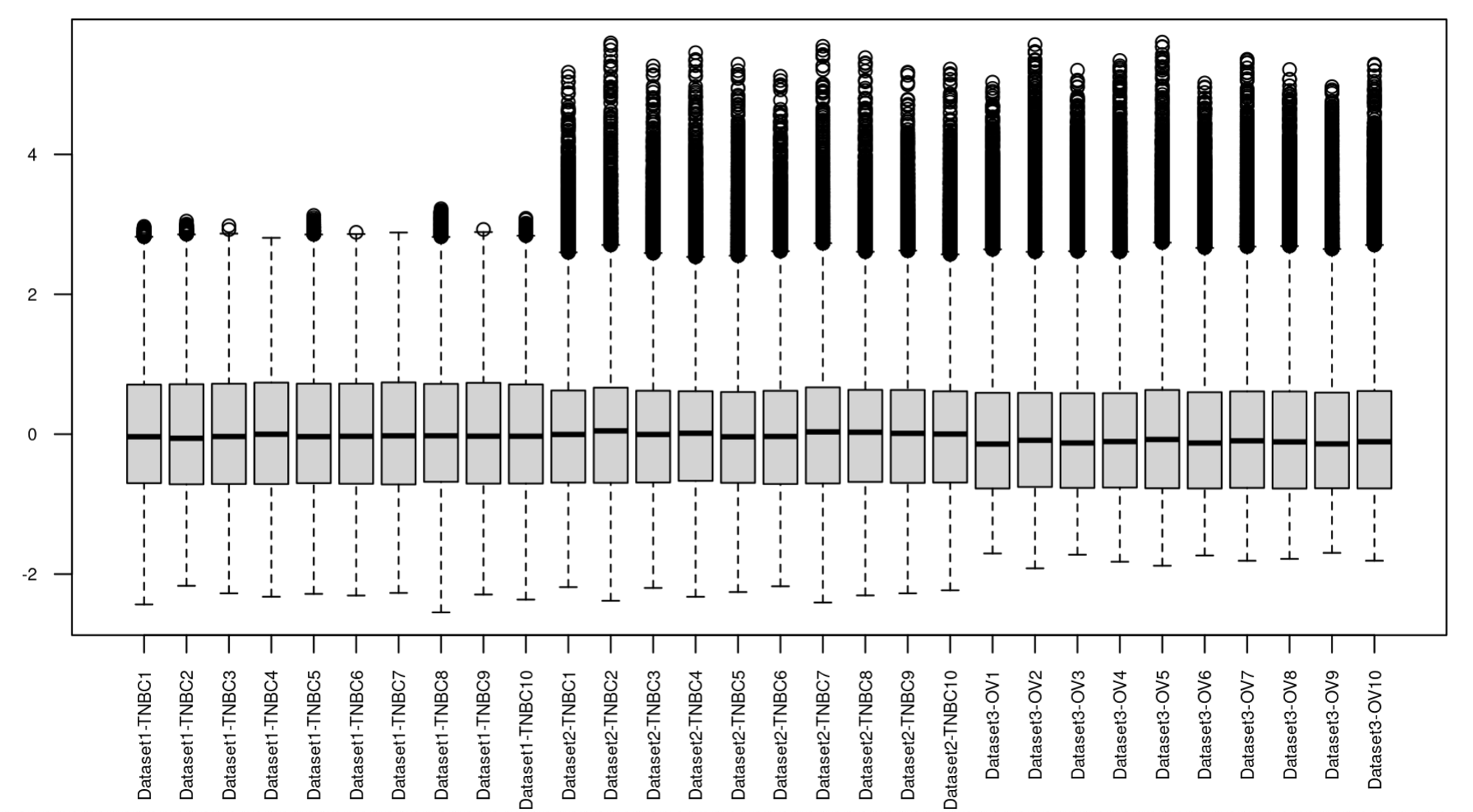
是不是看起来更整齐了!仔细看上去,不同数据集之间还是有显著差异的!
-
聚类
我们也可以将样本聚类查看其相似性,用聚类热图或者聚类树来展示都可以!
# 聚类,我们这里画个聚类树吧!而且因为数据量过大,我们截取一部分进行展示好不好!好! tmp_data <- dist(as.data.frame(t(exp_all[240:321, ]))) clustering <- hclust(tmp_data, method = "average") plot(clustering)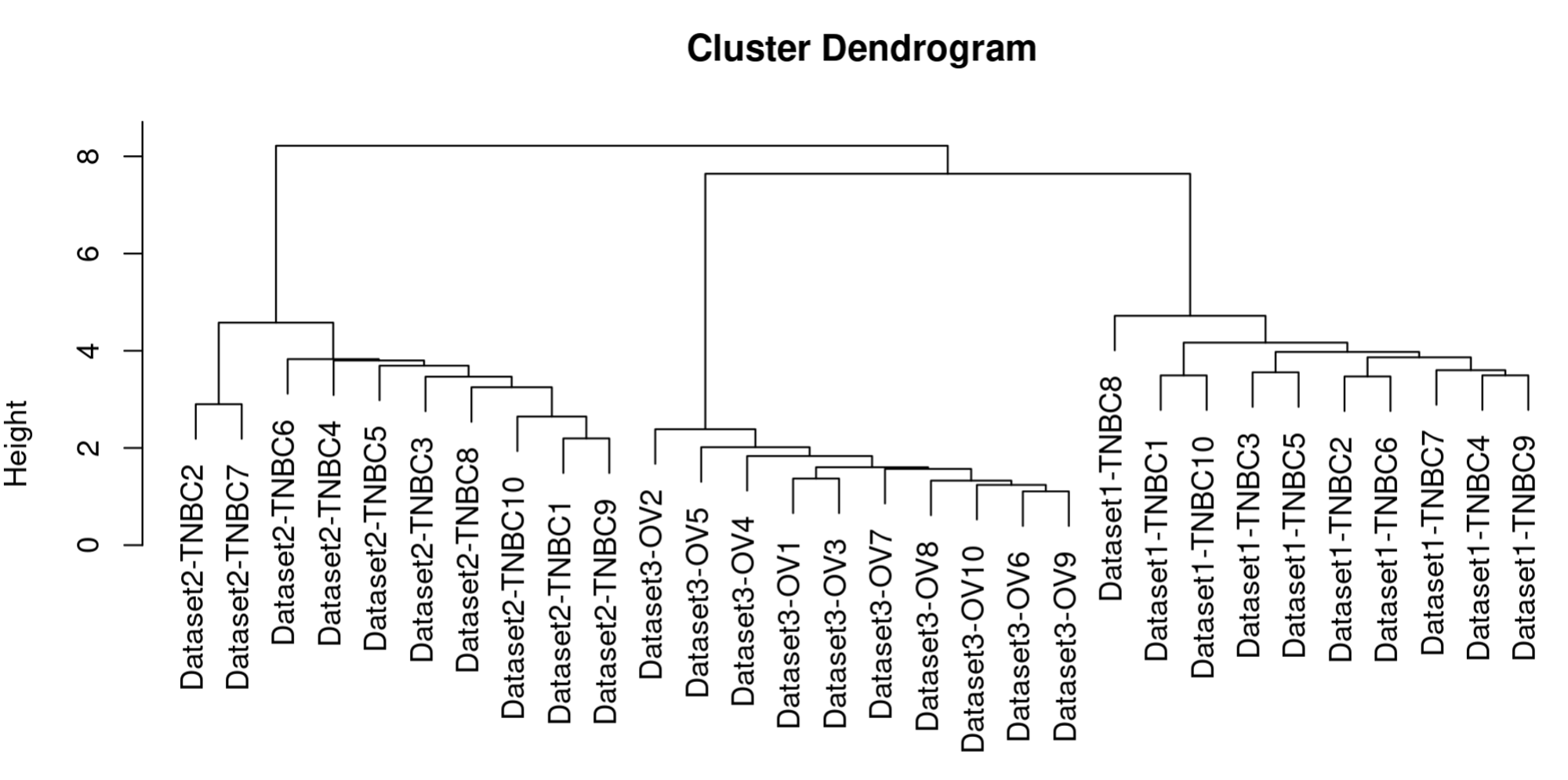
居然超级显著!三个数据集被聚成了三大类!
统计方法鉴定批次效应
接下来我们用统计方法来检测批次效应。常用的方法包括方差分析(anova)、线性混合效应模型(mixed effects models)、主成分分析(pca)等。这些方法可以帮助确定批次效应是否显著,并提供量化的结果。我们这里就展示一下pca可视化的结果吧!
# pca
# 这里我们先获取分组信息
group_list <- data.frame(
sample = colnames(exp_all), c(rep("dataset1-tnbc", 10), rep("dataset2-tnbc", 10), rep("dataset3-ov", 10)))
rownames(group_list) <- group_list$sample
colnames(group_list)[2] <- "dataset"
group <- factor(group_list$dataset)
# pca可视化
library(tinyarray)
draw_pca(exp = exp_all, group_list = group)
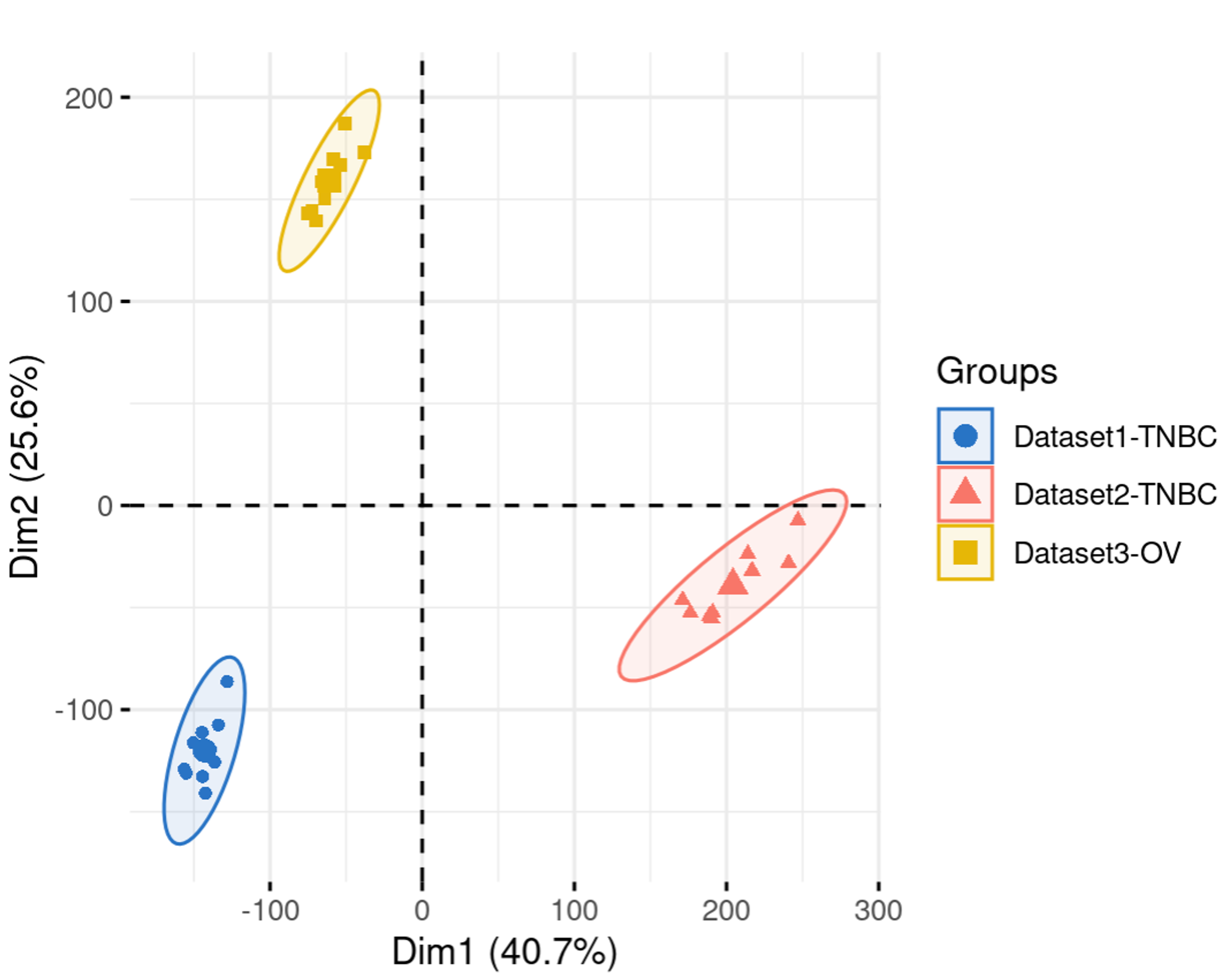
如何去除批次效应
接下来,我们就正式进入批次处理的核心部分啦!
sva包的combat函数
总的来说,combat是一种用于调整批次效应的方法,它采用参数或非参数经验贝叶斯模型。输入数据为标准化后的表达矩阵,通常用于处理芯片数据,有些教程认为它也适用于rna-seq的fpkm/tpm数据。combat_seq则是combat框架的改进版本,专门设计用于处理rna-seq的count数据。
############################### 去除批次效应 ################################
############################### sva的combat ################################
library(sva)
exp_all_combat <- combat(exp_all, batch = group_list$dataset) # batch为批次信息
我们来看看批次效应是否被去除了嘞!
# 查看去除批次效应的结果如何
# 箱线图2.0
boxplot(exp_all_combat, las = 2, cex.axis = 0.6)
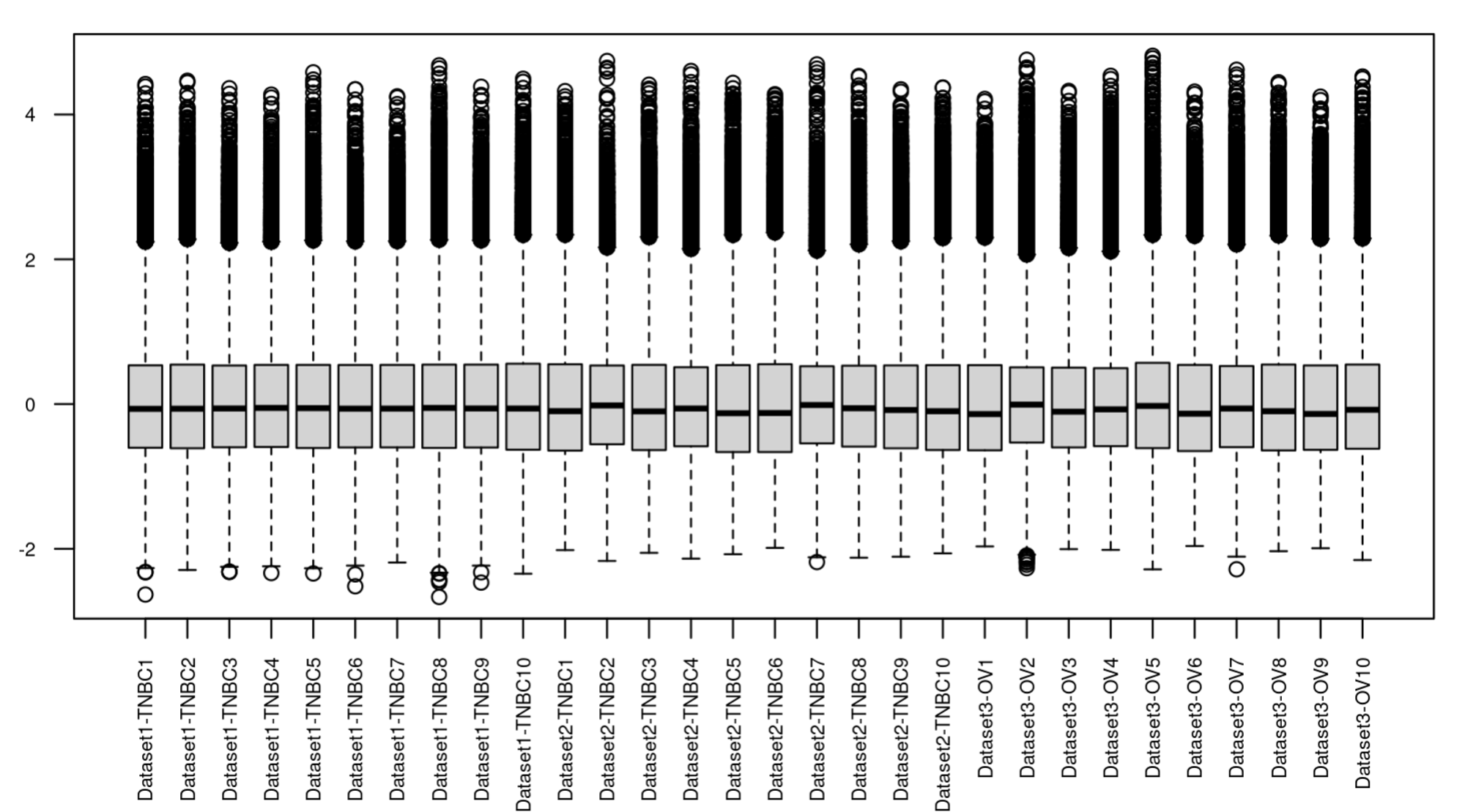
比之前更整齐了!
# 聚类树,还是截取部分展示
tmp_data <- dist(as.data.frame(t(exp_all_combat[240:321, ])))
clustering <- hclust(tmp_data, method = "average")
plot(clustering)
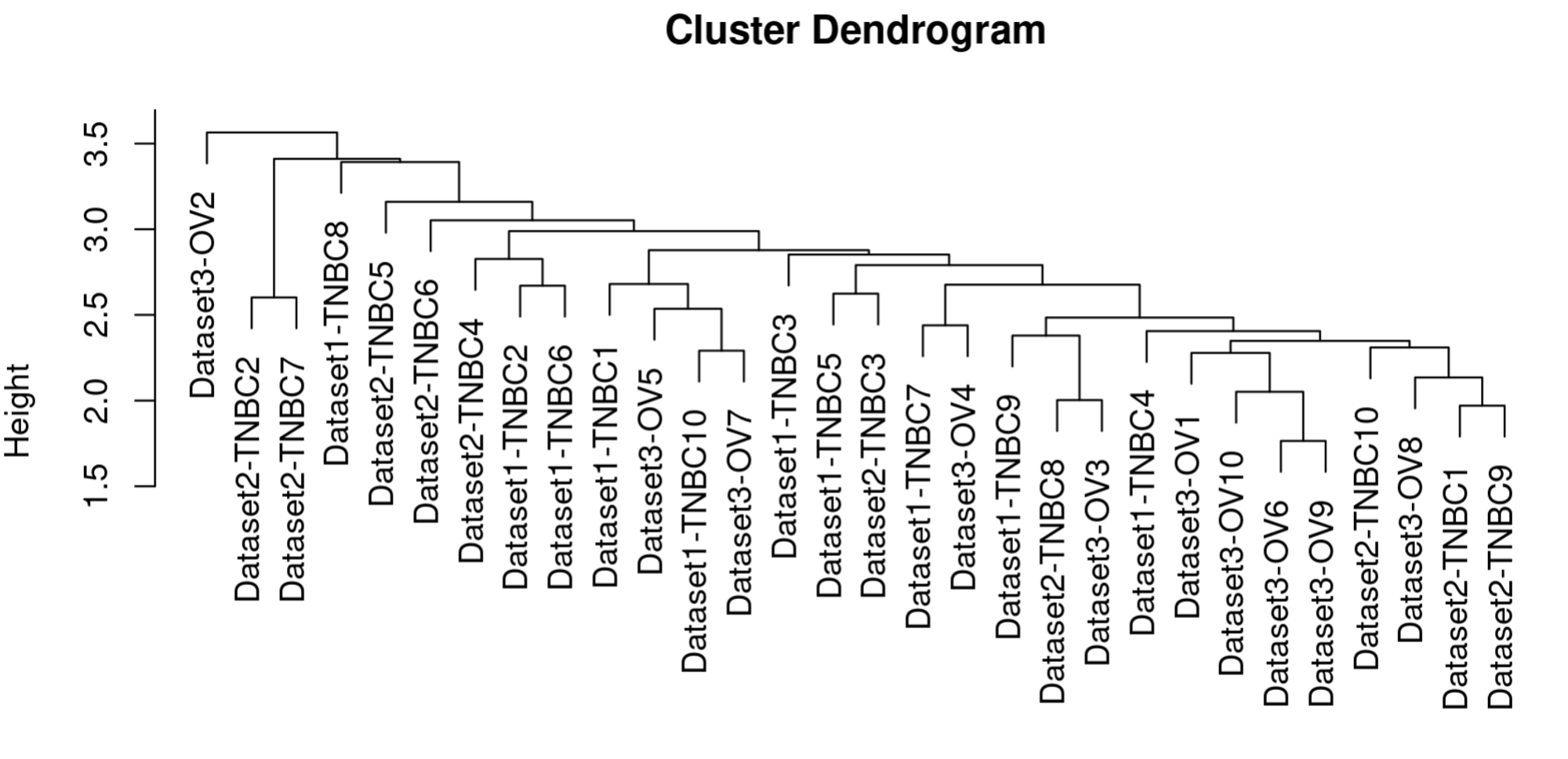
可以看到三个数据集的样本都在一个大群啦!
# pca可视化
library(tinyarray)
draw_pca(exp = exp_all_combat, group_list = group)
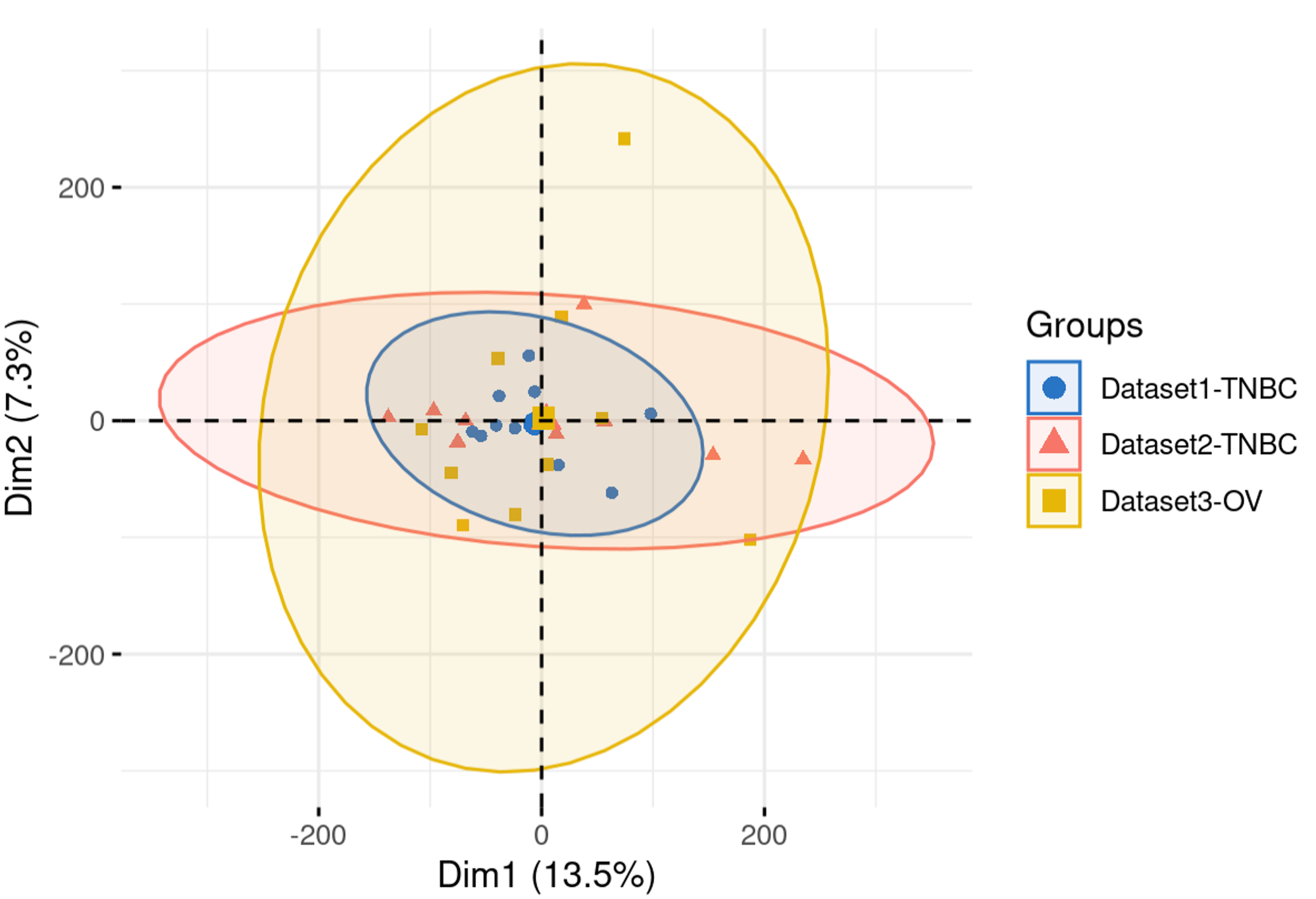
可以看到三个数据集的样本都混在一起啦!
说明咱们这波批次效应的处理非常成功呐!但是有个问题,乳腺癌和卵巢癌(也就是tnbc和ov),它们不该混在一起呀!它俩原本就是有生物学差异在的!这就说明我们现在矫枉过正啦!所以原本应该存在的分组也无法展现出来啦!
不过不要慌!combat里面有个mod选项,可以用来指定分组(比如肿瘤和正常、给药和对照等等,我们这里就是tnbc和ov),指定后,就可以告诉combat,样本中的有些分组,本身就是有差别的,你不要给我矫枉过正了哈!你得给我保留它们原本生物学上的差异哟!
来!咱们试试看!
**# 指定分组进行批次处理
# 指定分组信息
group_list_ori <- data.frame(
sample = colnames(exp_all), c(rep("tnbc", 19), rep("ov", 11)))
# 这里要跟大家解释一句,理论上应该是前20个是tnbc,后10个是ov
# 但我这里设成了前19个为tnbc,主要是因为我的数据集选择问题
# 正常来讲应该是不同的数据集中,都存在分组
# 比如在数据集a中存在肿瘤与正常两类样本,数据集b中也存在肿瘤与正常两类样本
# 而我找的是三个数据集,每个数据集中只包含一类样本
# 所以就导致函数会检测到批次和模型中的某个协变量之间存在混淆
# 也就是说这个协变量与批次效应存在相关性
# combat在调整批次效应时,要求协变量与批次独立,否则就可能引起混淆
# 所以这里我就擅自把tnbc数据集中的某个样本类型改为了ov以保证combat正常运行
# 我的锅!我在选择示例数据集的时候就该想到的!我的锅我的锅我的锅!我道歉!
# 其实我们一般是不会遇到这类问题的,所以按照自己的数据正常跑就可以!
# 大家尽管放心啦!!!
rownames(group_list_ori) <- group_list_ori$sample
colnames(group_list_ori)[2] <- "type"
group_ori <- as.factor(group_list_ori$type)
group_ori <- factor(group_list_ori$type, levels = c("tnbc", "ov"))
# 批次处理
exp_all_combat_ori <- combat(exp_all, batch = group_list$dataset, mod = group_ori)**
这里为了方便我就只展示pca结果了哈,有兴趣的小伙伴也可以自行跑一下箱线图、聚类结果等等!
# pca可视化
library(tinyarray)
draw_pca(exp = exp_all_combat_ori, group_list = group)
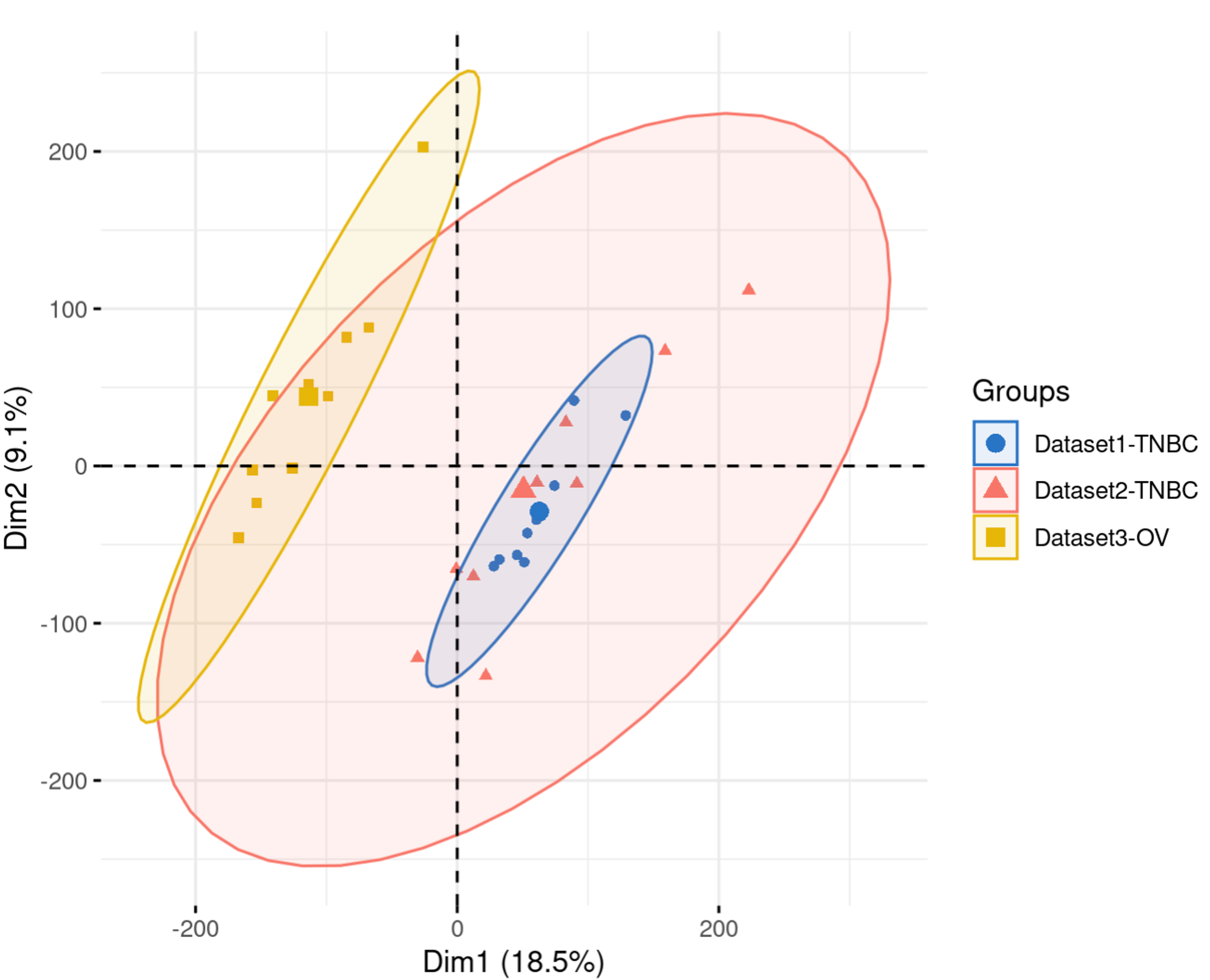
哇!这里我们可以观察到,来自不同数据集的tnbc样本都被分到了一起!而tnbc和ov两组样本则被很好的分开啦!这说明我们的批次效应去除成功!且没有过度矫正,保留了样本之间原本应该存在的生物学差异!
所以说呀,指定分组还是很必要滴!大家不要忘记哟!
limma包的removebatcheffect函数
除了sva的combat函数,limma包的removebatcheffect函数也可以用于去除批次效应。
########################### limma的removebatcheffect ############################
library(limma)
# 这里我们直接使用前面已经整理完毕的分组信息
mod <- model.matrix(~factor(group_list_ori$type))
exp_all_limma <- removebatcheffect(exp_all, batch = group_list$dataset, design = mod)
# pca可视化
library(tinyarray)
draw_pca(exp = exp_all_limma, group_list = group)
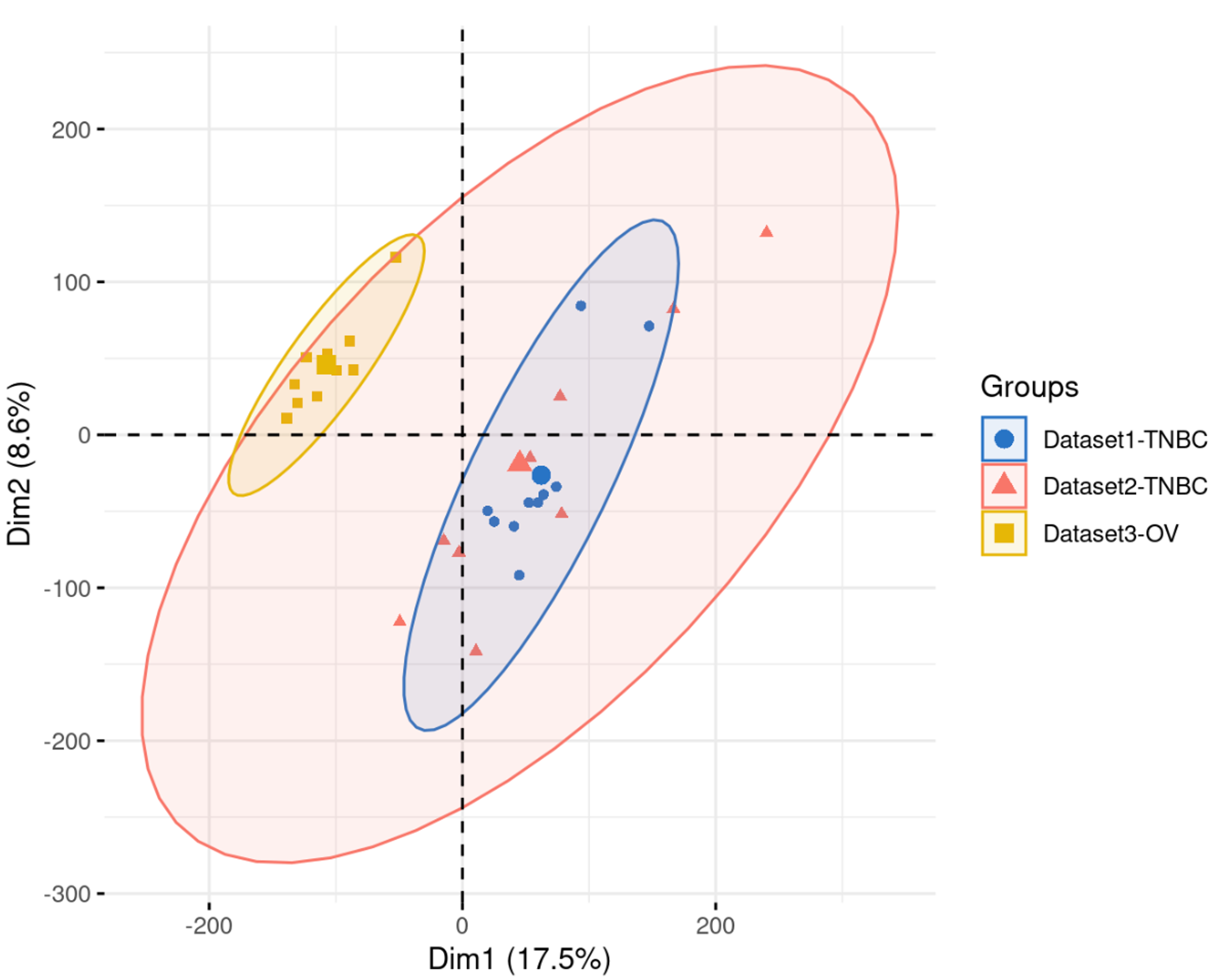
效果还阔以哈!
其实deseq2包也可以用来进行批次处理,不过它只能在做差异分析的时候顺便把批次效应去除,不能单独去除批次效应,而且效果嘛,就那样叭!
最后!咱们总结一下!
总结
在生物学研究中,面临实验或研究中常见的批次效应时,合理的数据处理方法至关重要。在r中,我们可以利用强大的工具包如sva、limma和deseq2等来处理批次效应,确保最终的分析结果更加可靠和可重复。
通过阅读全文,我们了解到批次效应可能对数据产生的系统性变异,干扰了对生物学差异的准确识别。我们学习了鉴定批次效应是否存在的方法,包括可视化分析和统计分析。针对批次效应的处理,我们介绍了不同包的方法。
sva包提供了combat和combat_seq函数,combat函数适用于芯片数据,其输入数据需要进行转换或者标准化;而combat_seq函数是专门针对rna-seq设计的,它的输入可以是 count数据,输出仍是一个counts矩阵。limma包的removebatcheffect函数适用于处理芯片设计的数据,因此不能直接使用count数据,需要对输入数据进行标准化处理。deseq2包是在进行差异分析的同时考虑批次效应。
最后,我们强调了在处理批次效应时需要谨慎选择方法,特别是要考虑到样本的生物学差异。适当的分组信息的指定,如在combat中使用的mod选项,有助于保留原始生物学差异,防止过度校正!
偷悄悄告诉你,俺更建议大家使用sva包进行批次处理哟!
参考资料
- https://www.plob.org/article/22574.html
- https://mp.weixin.qq.com/s/rcu84ycsmx4m0eqfsmmqdq
- https://blog.csdn.net/qazplm12_3/article/details/107925734
- https://www.jianshu.com/p/4c0734c3473c
- https://zhuanlan.zhihu.com/p/539507005
- https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0017238
那今天的分享就到这里啦!我们下期再见哟!
最后顺便给自己推荐一下嘿嘿嘿!
如果我的分享对你有用的话,欢迎关注点赞在看转发分享阿巴阿巴阿巴阿巴巴巴!这可是我的第一原动力!
蟹蟹你们的喜欢和支持!!!
啊对!如果小伙伴们有需求的话,也可以加入我们的交流群:一定要知道 | 我们的生信交流群终于来啦!
后续这个链接可能会更新,如果小伙伴点开它之后发现,咦,怎么失效啦!不要慌!咱们辛苦一下动动小手去公众号主页的作者精选那里,会有一篇同名的文章,点进去就是啦!

发表评论