文章目录
一、支持向量机概述
支持向量机(svm)是一种在机器学习领域广泛使用的算法,以其在较少计算资源下提供显著准确性的特点而受到青睐。svm 可用于分类和回归任务,但在分类问题中应用最为广泛。
什么是支持向量机?
支持向量机的目标是在 n n n 维空间( n n n 为特征数)中找到一个能够明确区分数据点的超平面。该超平面使得不同类别的数据点被分开,并且尽可能远离超平面,从而确保分类的稳健性。
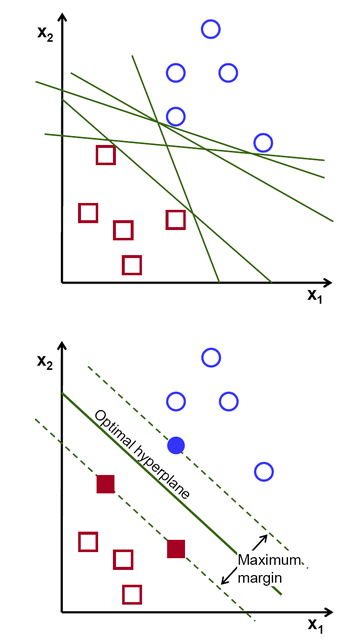
为了实现数据点的有效分离,可能存在多个超平面。我们的目标是选择一个具有最大边距的超平面,即两个类别之间的最大距离。最大化边距有助于提高分类的准确性。
超平面和支持向量

超平面是划分数据点的决策边界。位于超平面两侧的数据点可以被分为不同的类别。超平面的维度取决于特征的数量:如果输入特征为 2,则超平面是直线;如果特征为 3,则超平面是二维平面。当特征数量超过 3 时,超平面变得难以直观理解。
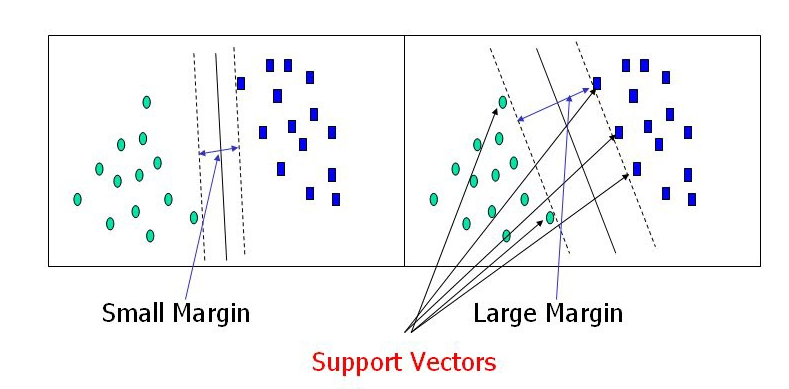
支持向量是指那些离超平面最近的点,这些点影响了超平面的位置和方向。通过这些支持向量,我们可以最大化分类器的边距。删除支持向量会改变超平面的位置,因此它们对构建 svm 至关重要。
大边距直觉
在逻辑回归中,我们使用 s 型函数将线性函数的输出值压缩到 [0,1] 范围内,并根据阈值(0.5)分配标签。而在 svm 中,我们使用线性函数的输出值来决定分类:如果输出大于 1,则属于一个类;如果输出为 -1,则属于另一个类。svm 通过将输出值的阈值设为 1 和 -1,形成了边际范围 [-1,1]。
二、数据预处理与可视化
使用支持向量机来预测癌症诊断的良恶性。
数据集的基本信息
- 特征数为30个,例如:
- 半径(从中心到周长点的距离平均值)
- 纹理(灰度值的标准偏差)
- 周长
- 面积
- 平滑度(半径长度的局部变化)
- 紧凑度(周长^2 / 面积 - 1.0)
- 凹度(轮廓凹陷部分的严重程度)
- 凹点(轮廓凹陷部分的数量)
- 对称性
- 分形维数(“海岸线近似” - 1)
- 数据集包含 569 个样本,类别分布为 212 个恶性样本和 357 个良性样本。
- 目标类别:
- 恶性
- 良性
导入必要的库
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.set_style('whitegrid')
加载数据集
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
# 创建 dataframe
col_names = list(cancer.feature_names)
col_names.append('target')
df = pd.dataframe(np.c_[cancer.data, cancer.target], columns=col_names)
df.head()
数据概况
df.info()print(cancer.target_names)
# ['malignant', 'benign']
# 数据描述:
df.describe()
# 统计摘要:
df.info()
数据可视化
特征对的散点图矩阵
sns.pairplot(df, hue='target', vars=[
'mean radius', 'mean texture', 'mean perimeter', 'mean area',
'mean smoothness', 'mean compactness', 'mean concavity',
'mean concave points', 'mean symmetry', 'mean fractal dimension'
])
类别分布条形图
sns.countplot(x=df['target'], label="count")
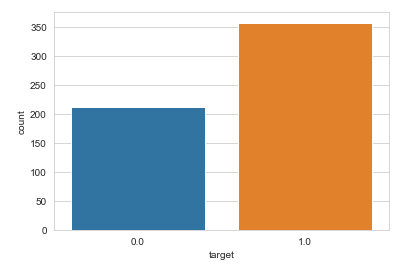
平均面积与平均光滑度的散点图
plt.figure(figsize=(10, 8))
sns.scatterplot(x='mean area', y='mean smoothness', hue='target', data=df)
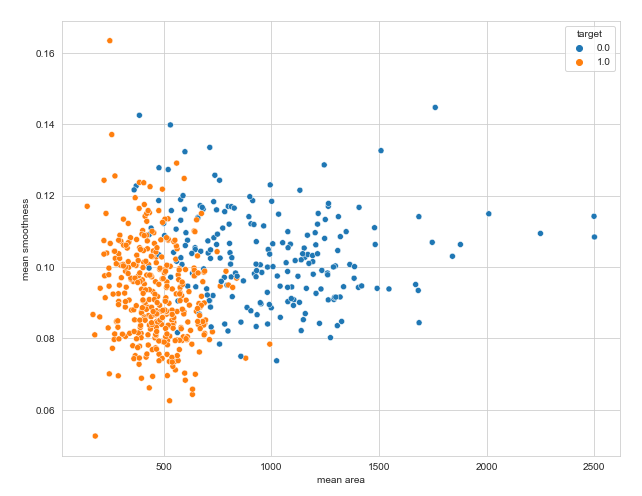
变量之间的相关性热图
plt.figure(figsize=(20,10))
sns.heatmap(df.corr(), annot=true)
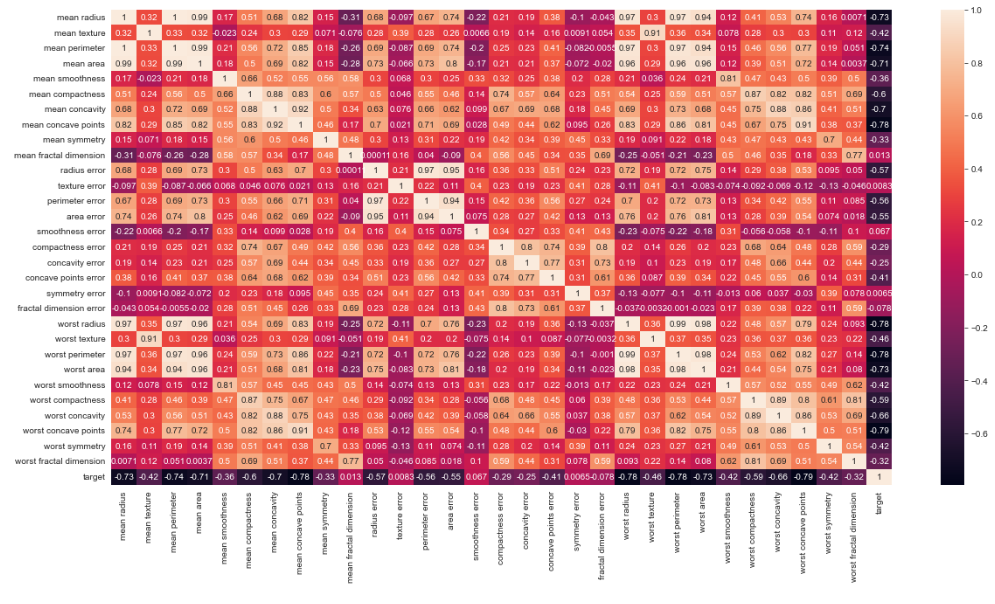
三、模型训练(问题解决)
在机器学习中,模型训练是寻找问题解决方案的关键步骤。下面我们将介绍如何使用 scikit-learn 进行模型训练,并展示支持向量机(svm)在不同内核下的性能表现。
数据准备与预处理
首先,我们需要准备和预处理数据。以下是数据预处理的代码示例:
from sklearn.model_selection import cross_val_score, train_test_split
from sklearn.pipeline import pipeline
from sklearn.preprocessing import standardscaler, minmaxscaler
x = df.drop('target', axis=1)
y = df.target
print(f"'x' shape: {x.shape}")
print(f"'y' shape: {y.shape}")
# 'x' shape: (569, 30)
# 'y' shape: (569,)
pipeline = pipeline([
('min_max_scaler', minmaxscaler()),
('std_scaler', standardscaler())
])
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=42)
在代码中,我们使用 minmaxscaler 和 standardscaler 对数据进行缩放。数据被分为训练集和测试集,其中 30% 的数据用于测试。
评估模型性能
为了评估模型的性能,我们定义了一个 print_score 函数,该函数可以输出训练和测试结果的准确率、分类报告和混淆矩阵:
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report
import pandas as pd
def print_score(clf, x_train, y_train, x_test, y_test, train=true):
if train:
pred = clf.predict(x_train)
clf_report = pd.dataframe(classification_report(y_train, pred, output_dict=true))
print("train result:\n================================================")
print(f"accuracy score: {accuracy_score(y_train, pred) * 100:.2f}%")
print("_______________________________________________")
print(f"classification report:\n{clf_report}")
print("_______________________________________________")
print(f"confusion matrix: \n {confusion_matrix(y_train, pred)}\n")
else:
pred = clf.predict(x_test)
clf_report = pd.dataframe(classification_report(y_test, pred, output_dict=true))
print("test result:\n================================================")
print(f"accuracy score: {accuracy_score(y_test, pred) * 100:.2f}%")
print("_______________________________________________")
print(f"classification report:\n{clf_report}")
print("_______________________________________________")
print(f"confusion matrix: \n {confusion_matrix(y_test, pred)}\n")
支持向量机(svm)
支持向量机(svm)是一种强大的分类算法,其性能受超参数的影响。下面将介绍 svm 的主要参数及其对模型性能的影响:
- c 参数:控制正确分类训练点和拥有平滑决策边界之间的权衡。较小的 c c c(宽松)使误分类成本(惩罚)较低(软边距),而较大的 c c c(严格)使误分类成本较高(硬边距),迫使模型更严格地解释输入数据。
- gamma 参数:控制单个训练集的影响范围。较大的 γ \gamma γ 使影响范围较近(较近的数据点具有较高的权重),较小的 γ \gamma γ 使影响范围较广(更广泛的解决方案)。
- degree 参数:多项式核函数(
'poly')的度,被其他内核忽略。可以通过网格搜索来找到最佳超参数值。
线性核 svm
线性核 svm 适用于大多数情况,特别是当数据集具有大量特征时。以下是使用线性核 svm 的代码示例:
from sklearn.svm import linearsvc
model = linearsvc(loss='hinge', dual=true)
model.fit(x_train, y_train)
print_score(model, x_train, y_train, x_test, y_test, train=true)
print_score(model, x_train, y_train, x_test, y_test, train=false)
训练和测试结果如下:
训练结果:
accuracy score: 86.18%
_______________________________________________
classification report:
0.0 1.0 accuracy macro avg weighted avg
precision 1.000000 0.819079 0.861809 0.909539 0.886811
recall 0.630872 1.000000 0.861809 0.815436 0.861809
f1-score 0.773663 0.900542 0.861809 0.837103 0.853042
support 149.000000 249.000000 0.861809 398.000000 398.000000
_______________________________________________
confusion matrix:
[[ 94 55]
[ 0 249]]
测试结果:
accuracy score: 89.47%
_______________________________________________
classification report:
0.0 1.0 accuracy macro avg weighted avg
precision 1.000000 0.857143 0.894737 0.928571 0.909774
recall 0.714286 1.000000 0.894737 0.857143 0.894737
f1-score 0.833333 0.923077 0.894737 0.878205 0.890013
support 63.000000 108.000000 0.894737 171.000000 171.000000
_______________________________________________
confusion matrix:
[[ 45 18]
[ 0 108]]
多项式核 svm
多项式核 svm 适用于非线性数据。以下是使用二阶多项式核的代码示例:
from sklearn.svm import svc
model = svc(kernel='poly', degree=2, gamma='auto', coef0=1, c=5)
model.fit(x_train, y_train)
print_score(model, x_train, y_train, x_test, y_test, train=true)
print_score(model, x_train, y_train, x_test, y_test, train=false)
训练和测试结果如下:
训练结果:
accuracy score: 96.98%
_______________________________________________
classification report:
0.0 1.0 accuracy macro avg weighted avg
precision 0.985816 0.961089 0.969849 0.973453 0.970346
recall 0.932886 0.991968 0.969849 0.962427 0.969849
f1-score 0.958621 0.976285 0.969849 0.967453 0.969672
support 149.000000 249.000000 0.969849 398.000000 398.000000
_______________________________________________
confusion matrix:
[[139 10]
[ 2 247]]
测试结果:
accuracy score: 97.08%
_______________________________________________
classification report:
0.0 1.0 accuracy macro avg weighted avg
precision 0.967742 0.972477 0.97076 0.970109 0.970733
recall 0.952381 0.981481 0.97076 0.966931 0.970760
f1-score 0.960000 0.976959 0.97076 0.968479 0.970711
support 63.000000 108.000000 0.97076 171.000000 171.000000
_______________________________________________
confusion matrix:
[[ 60 3]
[ 2 106]]
径向基函数(rbf)核 svm
径向基函数(rbf)核适用于处理非线性数据。以下是使用 rbf 核的代码示例:
model = svc(kernel='rbf', gamma=0.5, c=0.1)
model.fit(x_train, y_train)
print_score(model, x_train, y_train, x_test, y_test, train=true)
print_score(model, x_train, y_train, x_test, y_test, train=false)
训练和测试结果如下:
训练结果:
accuracy score: 62.56%
_______________________________________________
classification report:
0.0 1.0 accuracy macro avg weighted avg
precision 0.0 0.625628 0.625628 0.312814 0.392314
recall 0.0 1.000000 0.625628 0.500000 0.625628
f1-score 0.0 0.769231 0.625628 0.384615 0.615385
support 149.0 249.0 0.625628 398.0 398.0
_______________________________________________
confusion matrix:
[[ 0 149]
[ 0 249]]
测试结果:
accuracy score: 64.97%
_______________________________________________
classification report:
0.0 1.0 accuracy macro avg weighted avg
precision 0.0 0.655172 0.649661 0.327586 0.409551
recall 0.0 1.000000 0.649661 0.500000 0.649661
f1-score 0.0 0.792453 0.649661 0.396226 0.628252
support 63.0 108.0 0.649661 171.0 171.0
_______________________________________________
confusion matrix:
[[ 0 63]
[ 0 108]]
总结
通过以上模型训练和评估过程,我们可以观察到不同 svm 内核的性能差异。线性核 svm 在准确性和训练时间上表现良好,适用于数据维度较高的情况。多项式核 svm 和 rbf 核 svm 在非线性数据上具有更好的表现,但在某些参数设置下可能会导致过拟合。选择合适的内核和超参数对于模型性能的提升至关重要。
四、svm 数据准备
数字输入:svm 假设输入数据为数字。如果输入数据为分类变量,可能需要将其转换为二进制虚拟变量(每个类别一个变量)。
二元分类:基本的 svm 适用于二元分类问题。虽然 svm 主要用于二元分类,但也有扩展版本用于回归和多类分类。
x_train = pipeline.fit_transform(x_train)
x_test = pipeline.transform(x_test)
模型训练与评估
以下展示了不同 svm 内核的训练和测试结果:
线性核 svm
print("=======================linear kernel svm==========================")
model = svc(kernel='linear')
model.fit(x_train, y_train)
print_score(model, x_train, y_train, x_test, y_test, train=true)
print_score(model, x_train, y_train, x_test, y_test, train=false)
训练结果:
accuracy score: 98.99%
_______________________________________________
classification report:
0.0 1.0 accuracy macro avg weighted avg
precision 1.000000 0.984190 0.98995 0.992095 0.990109
recall 0.973154 1.000000 0.98995 0.986577 0.989950
f1-score 0.986395 0.992032 0.98995 0.989213 0.989921
support 149.000000 249.000000 0.98995 398.000000 398.000000
_______________________________________________
confusion matrix:
[[145 4]
[ 0 249]]
测试结果
accuracy score: 97.66%
_______________________________________________
classification report:
0.0 1.0 accuracy macro avg weighted avg
precision 0.968254 0.981481 0.976608 0.974868 0.976608
recall 0.968254 0.981481 0.976608 0.974868 0.976608
f1-score 0.968254 0.981481 0.976608 0.974868 0.976608
support 63.000000 108.000000 0.976608 171.000000 171.000000
_______________________________________________
confusion matrix:
[[ 61 2]
[ 2 106]]
多项式核 svm
print("=======================polynomial kernel svm==========================")
from sklearn.svm import svc
model = svc(kernel='poly', degree=2, gamma='auto')
model.fit(x_train, y_train)
print_score(model, x_train, y_train, x_test, y_test, train=true)
print_score(model, x_train, y_train, x_test, y_test, train=false)
训练结果:
accuracy score: 85.18%
_______________________________________________
classification report:
0.0 1.0 accuracy macro avg weighted avg
precision 0.978723 0.812500 0.851759 0.895612 0.874729
recall 0.617450 0.991968 0.851759 0.804709 0.851759
f1-score 0.757202 0.893309 0.851759 0.825255 0.842354
support 149.000000 249.000000 0.851759 398.000000 398.000000
_______________________________________________
confusion matrix:
[[ 92 57]
[ 2 247]]
测试结果:
accuracy score: 82.46%
_______________________________________________
classification report:
0.0 1.0 accuracy macro avg weighted avg
precision 0.923077 0.795455 0.824561 0.859266 0.842473
recall 0.571429 0.972222 0.824561 0.771825 0.824561
f1-score 0.705882 0.875000 0.824561 0.790441 0.812693
support 63.000000 108.000000 0.824561 171.000000 171.000000
_______________________________________________
confusion matrix:
[[ 36 27]
[ 3 105]]
径向基函数(radial basis function)核 svm
print("=======================radial kernel svm==========================")
from sklearn.svm import svc
model = svc(kernel='rbf', gamma=1)
model.fit(x_train, y_train)
print_score(model, x_train, y_train, x_test, y_test, train=true)
print_score(model, x_train, y_train, x_test, y_test, train=false)
训练结果:
accuracy score: 100.00%
_______________________________________________
classification report:
0.0 1.0 accuracy macro avg weighted avg
precision 1.0 1.0 1.0 1.0 1.0
recall 1.0 1.0 1.0 1.0 1.0
f1-score 1.0 1.0 1.0 1.0 1.0
support 149.0 249.0 1.0 398.0 398.0
_______________________________________________
confusion matrix:
[[149 0]
[ 0 249]]
测试结果:
accuracy score: 63.74%
_______________________________________________
classification report:
0.0 1.0 accuracy macro avg weighted avg
precision 1.000000 0.635294 0.637427 0.817647 0.769659
recall 0.015873 1.000000 0.637427 0.507937 0.637427
f1-score 0.031250 0.776978 0.637427 0.404114 0.502236
support 63.000000 108.000000 0.637427 171.000000 171.000000
_______________________________________________
confusion matrix:
[[ 1 62]
[ 0 108]]
支持向量机超参数调优
from sklearn.model_selection import gridsearchcv
param_grid = {'c': [0.01, 0.1, 0.5, 1, 10, 100],
'gamma': [1, 0.75, 0.5, 0.25, 0.1, 0.01, 0.001],
'kernel': ['rbf', 'poly', 'linear']}
grid = gridsearchcv(svc(), param_grid, refit=true, verbose=1, cv=5)
grid.fit(x_train, y_train)
best_params = grid.best_params_
print(f"best params: {best_params}")
svm_clf = svc(**best_params)
svm_clf.fit(x_train, y_train)
print_score(svm_clf, x_train, y_train, x_test, y_test, train=true)
print_score(svm_clf, x_train, y_train, x_test, y_test, train=false)
训练结果:
accuracy score: 98.24%
_______________________________________________
classification report:
0.0 1.0 accuracy macro avg weighted avg
precision 0.986301 0.980159 0.982412 0.983230 0.982458
recall 0.966443 0.991968 0.982412 0.979205 0.982412
f1-score 0.976271 0.986028 0.982412 0.981150 0.982375
support 149.000000 249.000000 0.982412 398.000000 398.000000
_______________________________________________
confusion matrix:
[[144 5]
[ 2 247]]
测试结果:
accuracy score: 98.25%
_______________________________________________
classification report:
0.0 1.0 accuracy macro avg weighted avg
precision 0.983871 0.981651 0.982456 0.982761 0.982469
recall 0.968254 0.990741 0.982456 0.979497 0.982456
f1-score 0.976000 0.986175 0.982456 0.981088 0.982426
support 63.000000 108.000000 0.982456 171.000000 171.000000
_______________________________________________
confusion matrix:
[[ 61 2]
[ 1 107]]
五、主成分分析
pca 简介
主成分分析(pca)是一种通过将数据投影到较低维空间来实现线性降维的技术,具体步骤如下:
- 使用奇异值分解:通过奇异值分解将数据投影到低维空间。
- 无监督学习:pca 不需要标记数据来进行降维。
- 特征转换:尝试找出哪些特征可以解释数据中的最大差异。
pca 可视化
由于高维数据难以直接可视化,我们可以使用 pca 找到前两个主成分,并在二维空间中可视化数据。为了实现这一点,需要先对数据进行标准化,使每个特征的方差为单位方差。
from sklearn.preprocessing import standardscaler
from sklearn.model_selection import train_test_split
from sklearn.decomposition import pca
import matplotlib.pyplot as plt
# 数据标准化
scaler = standardscaler()
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=42)
x_train = scaler.fit_transform(x_train)
x_test = scaler.transform(x_test)
# pca 降维
pca = pca(n_components=2)
x_train = pca.fit_transform(x_train)
x_test = pca.transform(x_test)
# 可视化前两个主成分
plt.figure(figsize=(8,6))
plt.scatter(x_train[:,0], x_train[:,1], c=y_train, cmap='plasma')
plt.xlabel('first principal component')
plt.ylabel('second principal component')
plt.show()
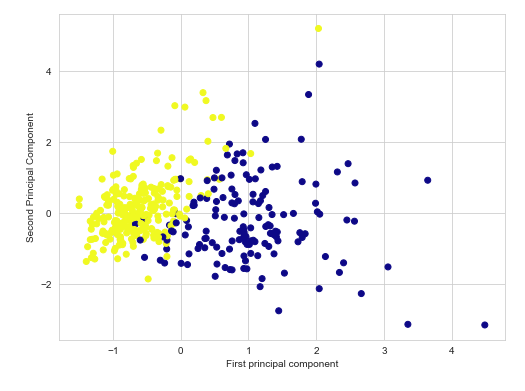
通过前两个主成分,我们可以在二维空间中轻松分离不同类别的数据点。
解释组件
降维虽然强大,但组件的含义较难直接理解。每个组件对应于原始特征的组合,这些组件可以通过拟合 pca 对象获得。
组件的相关属性包括:
- 成分得分:变换后的变量值。
- 载荷(权重):特征的组合权重。
- 数据压缩和信息保存:通过 pca 实现数据的压缩同时保留关键信息。
- 噪声过滤:降维过程中可以过滤掉噪声。
- 特征提取和工程:用于提取和构造新的特征。
支持向量机(svm)模型的参数调整
在使用支持向量机(svm)进行模型训练时,我们需要调整超参数以获得最佳模型。以下是使用网格搜索(gridsearchcv)调整 svm 参数的示例代码:
from sklearn.svm import svc
from sklearn.model_selection import gridsearchcv
# 定义参数网格
param_grid = {'c': [0.01, 0.1, 0.5, 1, 10, 100],
'gamma': [1, 0.75, 0.5, 0.25, 0.1, 0.01, 0.001],
'kernel': ['rbf', 'poly', 'linear']}
# 网格搜索
grid = gridsearchcv(svc(), param_grid, refit=true, verbose=1, cv=5)
grid.fit(x_train, y_train)
best_params = grid.best_params_
print(f"best params: {best_params}")
# 使用最佳参数训练模型
svm_clf = svc(**best_params)
svm_clf.fit(x_train, y_train)
训练结果:
accuracy score: 96.48%
_______________________________________________
classification report:
0.0 1.0 accuracy macro avg weighted avg
precision 0.978723 0.957198 0.964824 0.967961 0.965257
recall 0.926174 0.987952 0.964824 0.957063 0.964824
f1-score 0.951724 0.972332 0.964824 0.962028 0.964617
support 149.000000 249.000000 0.964824 398.000000 398.000000
_______________________________________________
confusion matrix:
[[138 11]
[ 3 246]]
测试结果:
accuracy score: 96.49%
_______________________________________________
classification report:
0.0 1.0 accuracy macro avg weighted avg
precision 0.967213 0.963636 0.964912 0.965425 0.964954
recall 0.936508 0.981481 0.964912 0.958995 0.964912
f1-score 0.951613 0.972477 0.964912 0.962045 0.964790
support 63.000000 108.000000 0.964912 171.000000 171.000000
_______________________________________________
confusion matrix:
[[ 59 4]
[ 2 106]]
六、总结
本文我们学习了以下内容:
- 支持向量机(svm):了解了 svm 的基本概念及其在 python 中的实现。
- svm 核函数:包括线性、径向基函数(rbf)和多项式核函数。
- 数据准备:如何为 svm 算法准备数据。
- 超参数调整:通过网格搜索调整 svm 的超参数。
- 主成分分析(pca):如何使用 pca 降低数据的复杂性,并在 scikit-learn 中进行重用。




发表评论