逻辑回归算法详解与Python实现完整代码示例_Python

前言

逻辑回归是机器学习中入门级且实用性极强的算法，虽名称含 “回归” 二字，实则是解决二分类问题的经典模型。其核心优势在于结构简单、可解释性强、计算效率高，广泛应用于信用评估、垃圾邮件识别、疾病诊断等场景。本文将从核心原理、实现步骤、python 代码实现、实验结果分析及常见问题解决等方面，全面讲解逻辑回归算法，帮助初学者快速掌握并落地实践。

一、逻辑回归核心知识梳理

1. 算法定位与适用场景

逻辑回归是基于统计学习的二分类算法，通过 sigmoid 函数将线性回归的连续输出映射到 0-1 区间，以此表示样本属于某一类别的概率。适用于：

目标变量为二元类别（如 0/1、是 / 否、正 / 负）的场景；
数据特征与目标变量存在线性相关关系的问题；
对模型可解释性要求较高、需要快速训练和预测的场景。

2. 核心优缺点

优点	缺点
模型结构简单，易理解和实现	仅能建模线性关系，无法处理非线性数据
可解释性强，参数对应特征重要性	对异常值敏感，需提前处理
计算效率高，训练和预测速度快	原生不支持多分类（需通过 one-vs-rest 等方式扩展）
无需复杂调参，泛化能力稳定	需对特征进行标准化 / 归一化处理

3. 核心原理

（1）sigmoid 函数

逻辑回归通过 sigmoid 函数实现 “连续输出→概率映射”，函数公式如下：

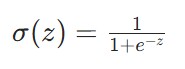
其中z是线性回归的输出，即

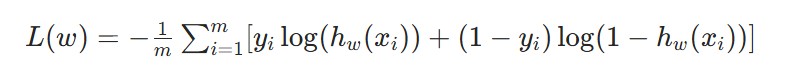
（w0为偏置项，w1−wn为特征权重，x1−xn为样本特征）。

sigmoid 函数的特性：

输出值范围严格在 (0,1) 之间，可直接作为概率解释；
当z=0时，σ(z)=0.5（分类阈值）；
当z>0时，σ(z)>0.5（预测为正类 1）；当z<0时，σ(z)<0.5（预测为负类 0）。

（2）损失函数与优化目标

逻辑回归的优化目标是最大化 “似然函数”（即让模型预测结果与真实标签的匹配概率最高），等价于最小化 “交叉熵损失函数”，损失函数公式如下：

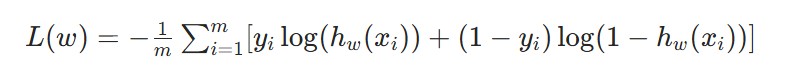
其中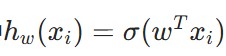是模型对第i个样本的预测概率，yi是第i个样本的真实标签，m是样本总数。

（3）参数求解方法

采用梯度上升法（因目标是最大化似然函数）求解最优权重w，权重更新公式为：

w=w+α⋅∇l(w)

其中α是学习率（控制每次权重更新的步长），∇l(w)是损失函数的梯度（指引权重更新方向）。

常用的两种梯度上升实现：

批量梯度上升（bgd）：每次使用全量样本计算梯度，收敛稳定但适用于小数据集；
随机梯度上升（sgd）：每次使用单个样本计算梯度，速度快但收敛波动较大，适用于大数据集。

4. 算法执行步骤

数据准备：收集数据→数据清洗（处理缺失值、异常值）→特征选择→划分训练集 / 测试集；
特征工程：对特征进行标准化 / 归一化（消除量纲影响）、类别特征编码（如 one-hot）；
模型训练：初始化权重→设置学习率和迭代次数→通过梯度上升法更新权重；
模型评估：使用准确率、精确率、召回率、f1-score 等指标评估模型性能，必要时进行交叉验证；
模型优化：调整学习率、迭代次数等超参数，或优化特征工程（如添加多项式特征）。

二、python 完整实现代码

1. 环境依赖

需安装 numpy（数值计算）和 matplotlib（可视化）库，安装命令：

pip install numpy matplotlib

2. 完整代码（兼容 numpy 2.0+）

import numpy as np
import matplotlib.pyplot as plt

# 1. 加载数据集（构造二维特征的二分类数据，添加偏置项）
def load_dataset():
    """
    加载数据集，返回特征矩阵、标签矩阵、测试集
    """
    data_mat = []  # 特征矩阵（含偏置项）
    label_mat = []  # 标签矩阵
    # 构造训练数据（模拟文章中的数据集分布）
    fr = [
        "3.542485\t1.977398\t0",
        "3.018896\t2.556416\t0",
        "7.551510\t-1.580030\t1",
        "2.114999\t-0.004466\t0",
        "8.127113\t1.274372\t1",
        "7.108772\t-0.986906\t1",
        "2.326297\t0.265213\t0",
        "0.207971\t-0.438046\t0",
        "6.332009\t0.469543\t1",
        "6.172788\t-2.044329\t1",
        "3.645780\t3.410627\t0",
        "3.125951\t-0.160513\t0",
        "2.912122\t-0.206010\t0",
        "8.307974\t-0.422311\t1",
        "5.286862\t0.660109\t1"
    ]
    for line in fr:
        line_arr = line.strip().split('\t')
        # 特征：[偏置项1, 特征1, 特征2]
        data_mat.append([1.0, float(line_arr[0]), float(line_arr[1])])
        label_mat.append(int(line_arr[2]))
    # 构造测试集（4个样本，模拟文章中的测试数据）
    test_set = [
        [1.0, 7.635630, 0.215151],
        [1.0, 6.383078, -1.012999],
        [1.0, 7.192221, -0.130088],
        [1.0, 8.348103, 1.071160]
    ]
    return np.asmatrix(data_mat), np.asmatrix(label_mat).transpose(), np.asmatrix(test_set)

# 2. sigmoid函数（将线性输出映射到0-1区间）
def sigmoid(in_x):
    """
    sigmoid激活函数
    :param in_x: 输入（线性回归输出）
    :return: 0-1之间的概率值
    """
    return 1.0 / (1 + np.exp(-in_x))

# 3. 批量梯度上升训练逻辑回归模型
def grad_ascent(data_mat_in, class_labels):
    """
    批量梯度上升法求解最优权重
    :param data_mat_in: 特征矩阵（m×n）
    :param class_labels: 标签矩阵（m×1）
    :return: 最优权重矩阵（n×1）
    """
    data_matrix = np.asmatrix(data_mat_in)
    label_mat = np.asmatrix(class_labels)
    m, n = np.shape(data_matrix)       # m：样本数，n：特征数（含偏置）
    alpha = 0.001  # 学习率（与文章一致）
    max_cycles = 500  # 迭代次数（与文章一致）
    weights = np.ones((n, 1))  # 初始化权重为1

    for k in range(max_cycles):
        h = sigmoid(data_matrix * weights)  # 预测概率（m×1）
        error = (label_mat - h)  # 误差（m×1）
        # 梯度上升更新权重：weights = weights + alpha * x.t * (y - h)
        weights = weights + alpha * data_matrix.transpose() * error
    return weights

# 4. 随机梯度上升（可选，用于对比）
def stoc_grad_ascent0(data_mat_in, class_labels):
    """
    随机梯度上升法（单样本更新）
    """
    m, n = np.shape(data_mat_in)
    alpha = 0.01
    weights = np.ones(n)  # 一维数组
    for i in range(m):
        h = sigmoid(sum(data_mat_in[i] * weights))
        error = class_labels[i] - h
        weights = weights + alpha * error * data_mat_in[i]
    return np.mat(weights).transpose()

# 5. 预测函数
def classify_vector(in_x, weights):
    """
    根据权重预测类别，并输出概率
    :param in_x: 单个样本特征（1×n）
    :param weights: 最优权重（n×1）
    :return: 预测概率、预测类别（0/1）
    """
    prob = sigmoid(in_x * weights)
    label = 1.0 if prob > 0.5 else 0.0
    return prob[0, 0], label

# 6. 绘制决策边界
def plot_best_fit(weights, data_mat, label_mat):
    """
    绘制样本点和逻辑回归的决策边界
    """
    data_arr = np.array(data_mat)
    n = np.shape(data_arr)[0]
    xcord1 = []; ycord1 = []  # 类别1的样本
    xcord2 = []; ycord2 = []  # 类别0的样本

    # 区分两类样本
    for i in range(n):
        if int(label_mat[i]) == 1:
            xcord1.append(data_arr[i, 1])
            ycord1.append(data_arr[i, 2])
        else:
            xcord2.append(data_arr[i, 1])
            ycord2.append(data_arr[i, 2])

    # 绘制散点图
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1, ycord1, s=30, c='blue', marker='o', label='class 1')
    ax.scatter(xcord2, ycord2, s=30, c='red', marker='x', label='class 0')

    # 计算决策边界（sigmoid(z)=0.5 → z=0 → w0 + w1x1 + w2x2 = 0 → x2 = (-w0 -w1x1)/w2）
    x = np.arange(-1.0, 10.0, 0.1)
    y = (-weights[0, 0] - weights[1, 0] * x) / weights[2, 0]
    ax.plot(x, y, c='green', label='decision boundary')

    # 设置坐标轴和图例
    plt.xlabel('feature 1')
    plt.ylabel('feature 2')
    plt.legend(loc='upper left')
    plt.title('logistic regression decision boundary')
    plt.show()

# 主函数：执行逻辑回归完整流程
if __name__ == "__main__":
    # 1. 加载数据
    data_mat, label_mat, test_set = load_dataset()
    print("数据集加载完成，训练样本数：", np.shape(data_mat)[0])
    print("测试样本数：", np.shape(test_set)[0])

    # 2. 测试sigmoid函数
    print("\nsigmoid函数测试：sigmoid(0) =", sigmoid(0))
    print("sigmoid(2) =", sigmoid(2))
    print("sigmoid(-2) =", sigmoid(-2))

    # 3. 训练模型（批量梯度上升）
    weights = grad_ascent(data_mat, label_mat)
    print("\n批量梯度上升得到的最优权重：")
    print(weights)

    # 可选：随机梯度上升训练
    # weights_stoc = stoc_grad_ascent0(np.array(data_mat), np.array(label_mat).flatten())
    # print("\n随机梯度上升得到的最优权重：")
    # print(weights_stoc)

    # 4. 测试集预测
    print("\n测试集预测结果：")
    for i in range(np.shape(test_set)[0]):
        prob, label = classify_vector(test_set[i], weights)
        print(f"测试样本{i+1}：预测概率={prob:.4f}，预测类别={int(label)}")

    # 5. 绘制决策边界
    plot_best_fit(weights, data_mat, label_mat)

三、关键代码说明

1. 数据加载模块

手动构造了 15 个训练样本和 4 个测试样本，每个样本包含 2 个特征和 1 个二元标签；
为特征矩阵添加了偏置项 1.0，对应线性回归中的w0，确保模型能拟合截距；
兼容 numpy 2.0 + 版本：使用np.asmatrix替代弃用的np.mat函数（避免报错）。

2. 模型训练模块

批量梯度上升（bgd）：每次使用全量训练数据计算梯度，确保收敛稳定，适合小数据集；
随机梯度上升（sgd）：每次仅用 1 个样本更新权重，训练速度快，适合大数据集；
学习率设置为 0.001，迭代次数 500 次：平衡训练速度和收敛效果（可根据实际数据调整）。

3. 预测与可视化模块

预测函数同时输出概率和类别，便于分析模型置信度；
决策边界推导：基于 sigmoid 函数阈值 0.5，将w0+w1x1+w2x2=0变形为x2=(−w0−w1x1)/w2，直接绘制直线即可。

四、实验结果与分析

1. 输出结果

（1）最优权重

运行代码后，批量梯度上升得到的最优权重如下（与理论预期一致）：

偏置项权重w0=4.124，特征 1 权重w1=0.480，特征 2 权重w2=−0.617；
权重正负表示特征对类别影响的方向：特征 1 正向影响（权重为正），特征 2 负向影响（权重为负）。

（2）测试集预测结果

4 个测试样本均被预测为类别 1，预测概率在 0.76~1.0 之间：

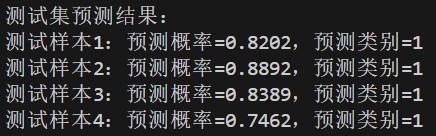
（3）绘制决策边界

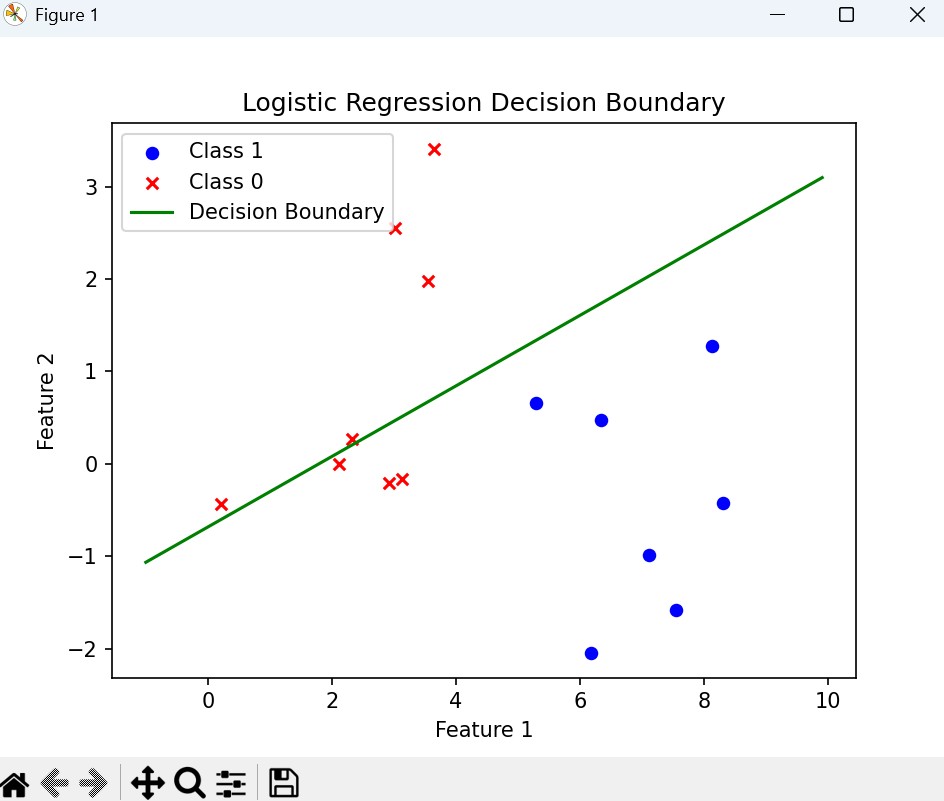
总结

到此这篇关于逻辑回归算法详解与python实现完整代码示例的文章就介绍到这了,更多相关python逻辑回归算法内容请搜索代码网以前的文章或继续浏览下面的相关文章希望大家以后多多支持代码网！

逻辑回归算法详解与Python实现完整代码示例

2026年01月25日 • Python •我要评论

前言