前言
本文介绍了欧氏距离、曼哈顿距离、切比雪夫距离、余弦距离、闵可夫斯基距离、汉明距离、编辑距离等七种常用距离度量方法的原理、意义与应用场景,并提供了 python 代码实现,帮助在数据科学、机器学习与工程实践中选择和使用合适的距离度量方法。
一、 欧式距离
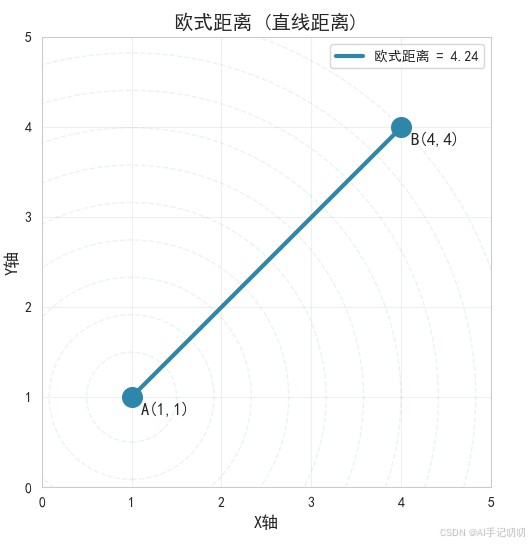
欧氏距离是“直线距离”。在二维或三维空间中,它就是两个点之间直接用尺子量出来的最短距离。
1. 核心思想
它源于欧几里得的几何学,衡量的是空间中两个点之间的“真实”直线长度。
2. 计算方法
- 二维空间(平面):计算两个点横坐标差的平方加上纵坐标差的平方,然后取平方根。
- 三维空间:计算两个点横坐标差的平方加上纵坐标差的平方再加上竖坐标差的平方,然后取平方根。
- n维空间(通用):计算两个点在各维度上数值差的平方之和,然后取平方根。
3. 示例代码
from math import sqrt
def euclidean_distance(p, q):
"""
计算欧式距离
p, q: 相同维度的数组或列表
"""
return sqrt(sum((px - qx) ** 2 for px, qx in zip(p, q)))
p = [1, 2, 3]
q = [4, 5, 6]
print(f"欧式距离: {euclidean_distance(p, q)}")
4. 主要特点
- 几何直观强:是最自然的距离度量方式,符合日常空间感知。
- 各向同性:在各个方向上具有相同的权重,适用于度量“真实”空间距离。
- 对异常值敏感:由于平方项的存在,个别维度的大差异会被放大。
- 计算复杂度中等:涉及平方、求和与开方运算。
5. 常见应用场景
- 空间几何:如计算两点之间的实际距离。
- 机器学习:knn、k-means等算法中常用的距离度量。
- 图像处理:如像素之间的颜色距离计算。
- 数据聚类与分类:在特征空间中度量样本相似性。
二、 曼哈顿距离
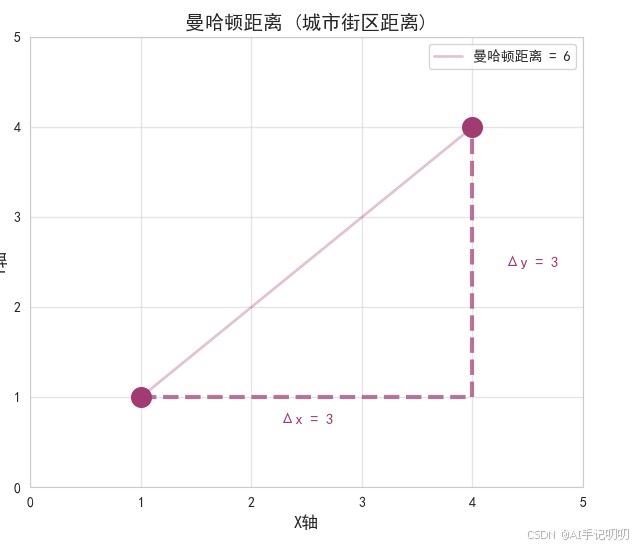
曼哈顿距离,也称为“城市街区距离”或“l1距离”,是指两点在标准坐标系上的绝对轴距总和。
1. 核心思想
来源于在网格状道路(如曼哈顿街区)中行走的最短路径,只能沿着水平和垂直方向移动,不能走斜线。
2. 计算方法
计算两个点在各维度上数值差的绝对值之和。
3. 示例代码
def manhattan_distance(p, q):
"""
计算曼哈顿距离
"""
return sum(abs(px - qx) for px, qx in zip(p, q))
# 示例
p = [1, 2, 3]
q = [4, 5, 6]
print(f"曼哈顿距离: {manhattan_distance(p, q)}")
4. 主要特点
- 非直线路径:适用于只能沿坐标轴方向移动的场景。
- 对异常值不敏感:相比欧氏距离,对个别维度的极端值不那么敏感。
- 计算简单高效:仅涉及绝对值和加法运算。
5. 常见应用场景
- 路径规划:如城市网格导航、机器人移动规划。
- 数据挖掘:在某些聚类或分类任务中,尤其是当特征空间具有明显网格结构时。
- 图像处理:如像素距离计算、图像压缩等。
三、 切比雪夫距离
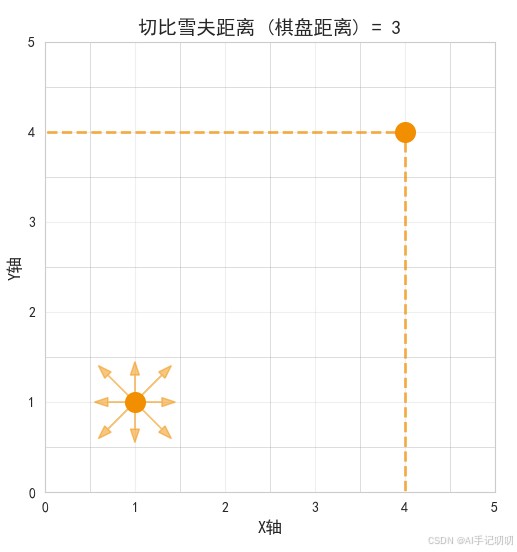
切比雪夫距离,也称为“棋盘距离”,是指两点之间各坐标数值差的最大值。
1. 核心思想
来源于国际象棋中“王”的移动方式,可以朝任意方向移动一格,因此在多维空间中体现为各维度差值中的最大值。
2. 计算方法
取两个点在各维度上数值差的绝对值中的最大值。
3. 示例代码
def chebyshev_distance(p, q):
"""
计算切比雪夫距离
"""
return max(abs(px - qx) for px, qx in zip(p, q))
# 示例
p = [1, 2, 3]
q = [4, 5, 6]
print(f"切比雪夫距离: {chebyshev_distance(p, q)}")
4. 主要特点
- 关注最大差异:仅由最大差异的维度决定距离。
- 适用于方形邻域:在多维空间中定义“超立方体”邻域。
- 计算简单:仅需比较和取最大值。
5. 常见应用场景
- 棋盘类游戏ai:如国际象棋、围棋的移动判断。
- 工业制造:在质量控制中检测最大偏差。
- 图像处理:用于边缘检测、形态学操作中的邻域定义。
四、余弦距离
1. 核心思想
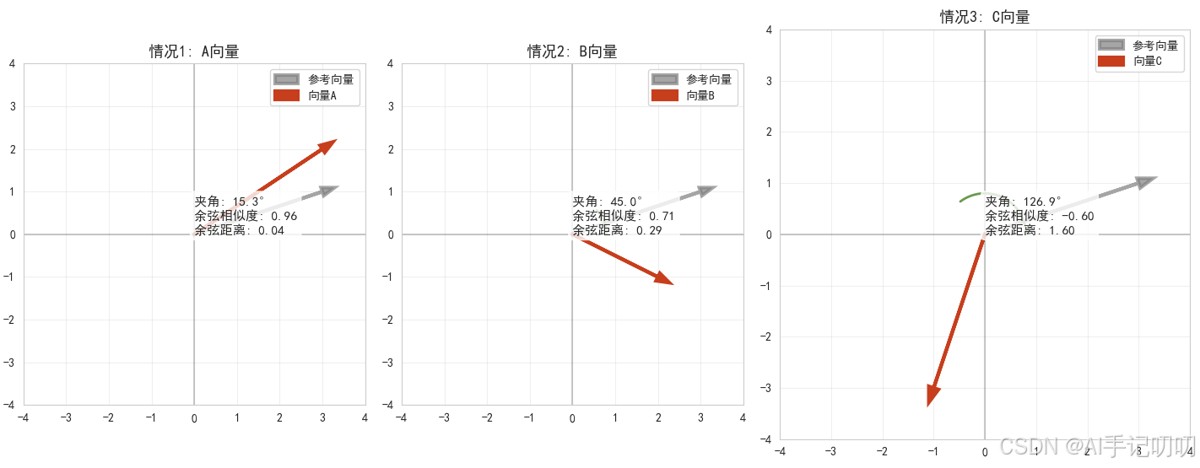
余弦距离用于衡量两个向量在方向上的差异,而不是位置或绝对长度。它基于向量夹角的余弦值,适用于高维稀疏向量比较,如文本相似性分析。
2. 计算方法
- 计算两个向量的点积(对应元素相乘后求和)
- 分别计算两个向量的模长(各元素平方和的平方根)
- 用点积除以两个模长的乘积,得到余弦相似度
- 余弦距离 = 1 - 余弦相似度
3. 示例代码
import numpy as np
from numpy.linalg import norm
def cosine_distance(a, b):
"""
计算余弦距离 = 1 - 余弦相似度
注:对于零向量,余弦相似度通常定义为0,因此余弦距离为1
"""
dot_product = np.dot(a, b)
norm_a = norm(a)
norm_b = norm(b)
if norm_a == 0 or norm_b == 0:
return 1.0 # 零向量的情况
cosine_sim = dot_product / (norm_a * norm_b)
return 1.0 - cosine_sim
# 示例
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
print(f"余弦距离: {cosine_distance(a, b)}")
4. 主要特点
- 方向敏感性:只关注向量方向,忽略长度差异
- 适合高维稀疏数据:对文本tf-idf向量等效果显著
- 归一化特性:结果在[0,2]或[0,1]之间
- 计算复杂度:中等,涉及点积和范数计算
5. 常见应用场景
- 文本相似度计算(信息检索、推荐系统)
- 文档聚类与分类
- 协同过滤推荐
- 高维数据相似性搜索
五、闵可夫斯基距离
1. 核心思想
闵可夫斯基距离是欧式距离和曼哈顿距离的一般化形式,通过参数 ( p ) 控制距离的计算方式。
2. 计算方法
- 计算两个点在各维度上数值差的绝对值的 p 次方
- 将这些 p 次方的值求和
- 对求和结果取 p 次方根
3. 特殊情况
- p = 1:曼哈顿距离
- p = 2:欧氏距离
- p → ∞:切比雪夫距离
4. 示例代码
from math import pow
def minkowski_distance(point1, point2, order=2):
"""
计算闵可夫斯基距离
参数:
point1, point2: 要比较的点(列表或数组)
order: 闵可夫斯基参数(order=1:曼哈顿,order=2:欧式,order=∞:切比雪夫)
"""
if order == float('inf'):
# 切比雪夫距离
return max(abs(p1 - p2) for p1, p2 in zip(point1, point2))
sum_power = sum(pow(abs(p1 - p2), order) for p1, p2 in zip(point1, point2))
return pow(sum_power, 1.0 / order)
# 示例
p = [1, 2, 3]
q = [4, 5, 6]
print(f"闵可夫斯基距离(order=1, 曼哈顿): {minkowski_distance(p, q, order=1)}")
print(f"闵可夫斯基距离(order=2, 欧式): {minkowski_distance(p, q, order=2)}")
print(f"闵可夫斯基距离(order=3): {minkowski_distance(p, q, order=3)}")
print(f"闵可夫斯基距离(order=∞, 切比雪夫): {minkowski_distance(p, q, order=float('inf'))}")
5. 主要特点
- 通用性强:通过参数调节适应不同场景
- 连续变化:距离特性随 p 值连续变化
- 对异常值的敏感性:当 p 值较大时,对异常值更敏感;p 值较小时,对异常值较不敏感。
- 计算复杂度:随 p 变化,一般高于曼哈顿距离
6. 常见应用场景
- 机器学习中的距离度量选择
- 模式识别与分类
- 参数化距离分析
- 多准则决策分析
六、汉明距离
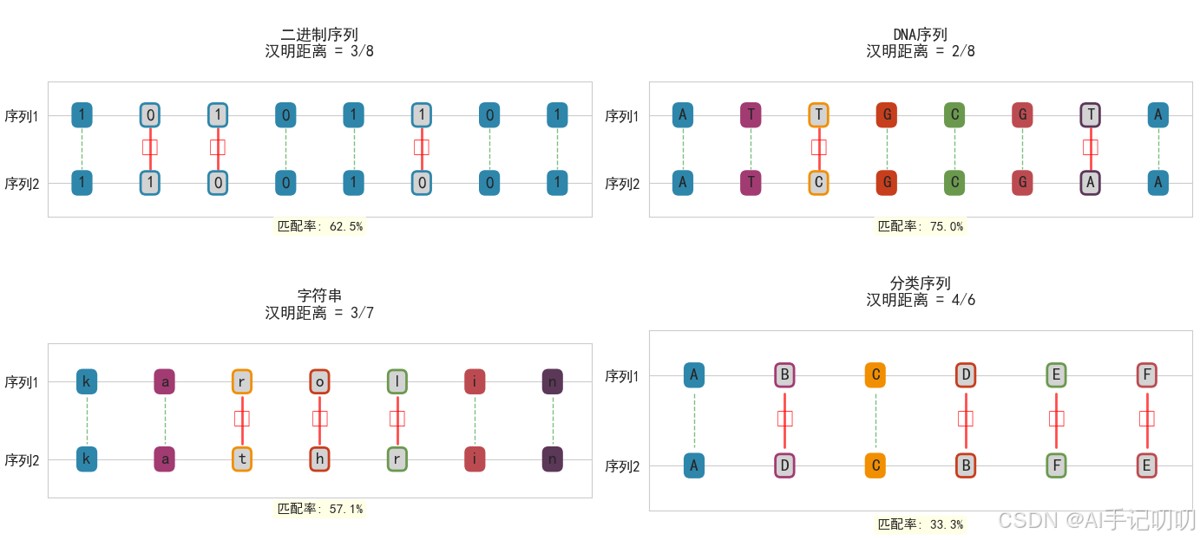
1. 核心思想
汉明距离用于比较两个等长字符串或序列的不同位置数量,主要用于编码理论和信息论。
2. 计算方法
比较两个字符串或序列对应位置上的字符或数值,统计不相等的位数的总数。
3. 示例代码
def hamming_distance(s1, s2):
"""
计算汉明距离(适用于等长序列)
"""
if len(s1) != len(s2):
raise valueerror("序列长度必须相等")
return sum(c1 != c2 for c1, c2 in zip(s1, s2))
# 示例(字符串)
s1 = "karolin"
s2 = "kathrin"
print(f"字符串汉明距离: {hamming_distance(s1, s2)}")
# 示例(二进制列表)
binary1 = [1, 0, 1, 0, 1]
binary2 = [0, 1, 0, 1, 0]
print(f"二进制汉明距离: {hamming_distance(binary1, binary2)}")
4. 主要特点
- 离散性:只比较对应位置是否相等
- 简单高效:适用于二进制或离散数据
- 无方向性:仅计数差异,不衡量差异大小
5. 常见应用场景
- 错误检测与纠正编码
- 基因组序列比对
- 网络数据包校验
- 二进制特征比较
七、编辑距离
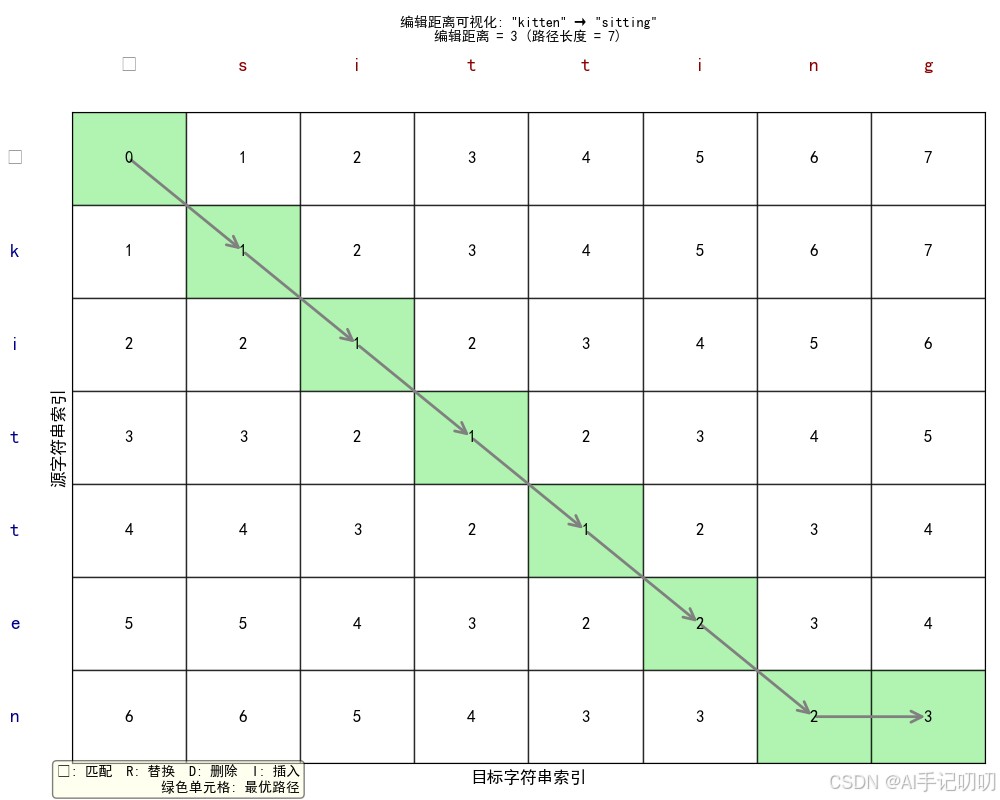
1. 核心思想
编辑距离衡量两个字符串之间的相似度,定义为将一个字符串转换为另一个字符串所需的最少编辑操作次数(插入、删除、替换)。
2. 计算方法
使用动态规划算法:
- 创建一个二维表格,行数=源字符串长度+1,列数=目标字符串长度+1
- 初始化第一行和第一列(从空字符串转换的代价)
- 逐行逐列填充表格:
- 如果字符相同,直接取左上角值(表示无需编辑)。
- 如果字符不同,取左方(删除)、上方(插入)、左上方(替换)三个值的最小值加1。
- 表格右下角的值即为编辑距离
3. 示例代码
def edit_distance(s1, s2):
"""
计算编辑距离(levenshtein距离)
"""
m, n = len(s1), len(s2)
dp = [[0] * (n + 1) for _ in range(m + 1)]
# 初始化边界条件
for i in range(m + 1):
dp[i][0] = i
for j in range(n + 1):
dp[0][j] = j
# 动态规划填表
for i in range(1, m + 1):
for j in range(1, n + 1):
if s1[i-1] == s2[j-1]:
dp[i][j] = dp[i-1][j-1] # 字符相同,无需编辑
else:
dp[i][j] = min(
dp[i-1][j] + 1, # 删除
dp[i][j-1] + 1, # 插入
dp[i-1][j-1] + 1 # 替换
)
return dp[m][n]
def normalized_edit_distance(s1, s2):
"""
计算归一化编辑距离(范围[0, 1])
"""
max_len = max(len(s1), len(s2))
if max_len == 0:
return 0.0
return edit_distance(s1, s2) / max_len
# 示例
s1 = "kitten"
s2 = "sitting"
print(f"编辑距离: {edit_distance(s1, s2)}") # 输出: 3
print(f"归一化编辑距离: {normalized_edit_distance(s1, s2):.4f}") # 输出: 0.4286
4. 主要特点
- 灵活性强:支持不等长字符串
- 操作敏感:区分插入、删除、替换
- 计算复杂度:o(m×n),可优化
- 归一化版本:编辑距离归一化到 [0,1] 区间
5. 常见应用场景
- 拼写检查与纠错
- 生物序列比对(dna/蛋白质)
- 自然语言处理(文本相似度)
- 模糊字符串匹配(数据清洗)
- 语音识别与语音转换
八、 比较
| 核心思想 | 计算复杂度 | 异常值敏感性 | 适用数据类型 | 应用场景 | 别名/类别 | |
|---|---|---|---|---|---|---|
| 欧式距离 | 两点之间的“直线距离” | 中等(平方、求和、开方) | 敏感(平方放大异常值) | 各向同性空间 | 几何距离、knn、聚类、图像处理 | l2距离、直线距离 |
| 曼哈顿距离 | 两点在网格路径上的“城市街区距离” | 低(绝对值、求和) | 较不敏感 | 网格/正交空间 | 路径规划、网格导航、图像处理、数据挖掘 | l1距离、城市街区距离 |
| 切比雪夫距离 | 两点在各维度上差异的最大值 | 低(比较、取最大值) | 依赖最大差异维度 | 最大差异主导空间 | 棋盘ai、质量控制、图像形态学 | 棋盘距离、l∞距离 |
| 余弦距离 | 向量方向相似性 | 中等 | 不敏感 | 高维稀疏向量 | 文本挖掘、推荐系统、文档聚类 | 余弦相似度的补 |
| 闵可夫斯基距离 | 参数化的通用距离族 | 中等(取决于p) | 敏感(p≠∞时) | 连续数值数据 | 参数化距离分析、机器学习 | minkowski距离族 |
| 汉明距离 | 离散序列差异计数 | 低 | 对位置差异敏感 | 等长序列 | 编码理论、基因组比对、错误检测 | 汉明差异 |
| 编辑距离 | 字符串转换的最少编辑操作数 | 中等(o(m×n),动态规划) | 对编辑位置敏感,对数值不敏感 | 字符串/序列(可不等长) | 拼写纠错、生物序列比对、文本相似度、模糊匹配 | levenshtein距离、字符串编辑距离 |
九、选择
- 欧式距离:最自然的空间距离,适用于物理空间或各向同性特征空间
- 曼哈顿距离:适用于网格路径、特征独立的场景
- 切比雪夫距离:关注最大差异的场景,如质量控制
- 余弦距离:适合文本、高维稀疏数据的方向比较
- 闵可夫斯基距离:需要灵活调整距离特性的参数化方法
- 汉明距离:离散序列、编码、二进制数据的比较
- 编辑距离:字符串处理、文本相似度、生物信息学
不同的距离度量适用于不同的数据特性和任务需求。在实际应用中,通常需要根据数据分布、特征关系和具体任务来选择合适的距离函数。
到此这篇关于python七种距离度量方法的文章就介绍到这了,更多相关python距离度量方法内容请搜索代码网以前的文章或继续浏览下面的相关文章希望大家以后多多支持代码网!






发表评论