1 振铃效应(ringingeffect)
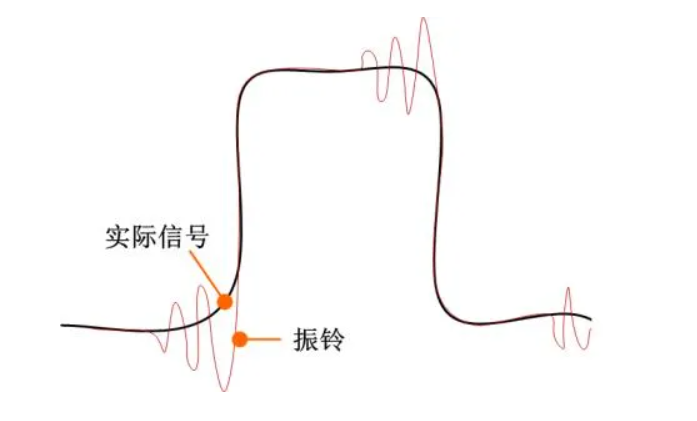
“图像处理中,对一幅图像进行滤波处理,若选用的频域滤波器具有陡峭的变化,则会使滤波图像产生‘振铃’,就是指输出图像的灰度剧烈变化处产生的震荡,就好像钟被敲击后产生的空气震荡。”(如下图)

(色差越大,出现色差地方越多,则振铃效应越明显)
% 读取图像
img = imread('1.jpg');
% 转换图像为灰度图
gray_img = rgb2gray(img);
% 计算图像的傅里叶变换
f = fftshift(fft2(double(gray_img)));
% 创建幅频低通滤波器
[m, n] = size(gray_img);
d0 = 30; % 截止频率
h = zeros(m, n);
for u = 1:m
for v = 1:n
d = sqrt((u - m/2)^2 + (v - n/2)^2);
if d <= d0
h(u, v) = 1;
end
end
end
% 应用滤波器
g = h .* f;
% 反傅里叶变换得到滤波后的图像
filtered_img = ifft2(ifftshift(g));
% 显示原始图像和滤波后的图像
figure;
subplot(1, 2, 1);
imshow(gray_img);
title('原始图像');
subplot(1, 2, 2);
imshow(abs(filtered_img), []);
title('滤波后的图像');下面就振铃效应的产生原因进行简要分析。
1.1 傅里叶变换
1.1.1 吉布斯现象
吉布斯现象如下图所示:
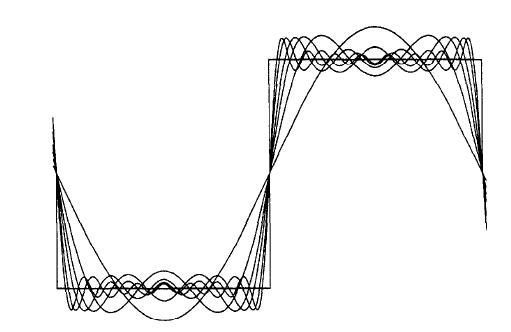
含义:一个不连续信号 x(t) 的傅里叶级数的截断近似 xn(t),一般来说,在接近不连续点处将呈现高频起伏和超量,而且,若在实际情况下利用这样一个近似式的话,就应该选择足够大的 n ,以保证这些起伏拥有的总能量可以忽略。当然,在极限情况下,近似误差的能量是零,而且一个不连续的信号(如方波)的傅里叶级数表示是收敛的。
1.1.2 傅里叶级数展开
我们来分析低通滤波器,不过是类似“窗”的样式,窗内的留下,窗外的滤除。
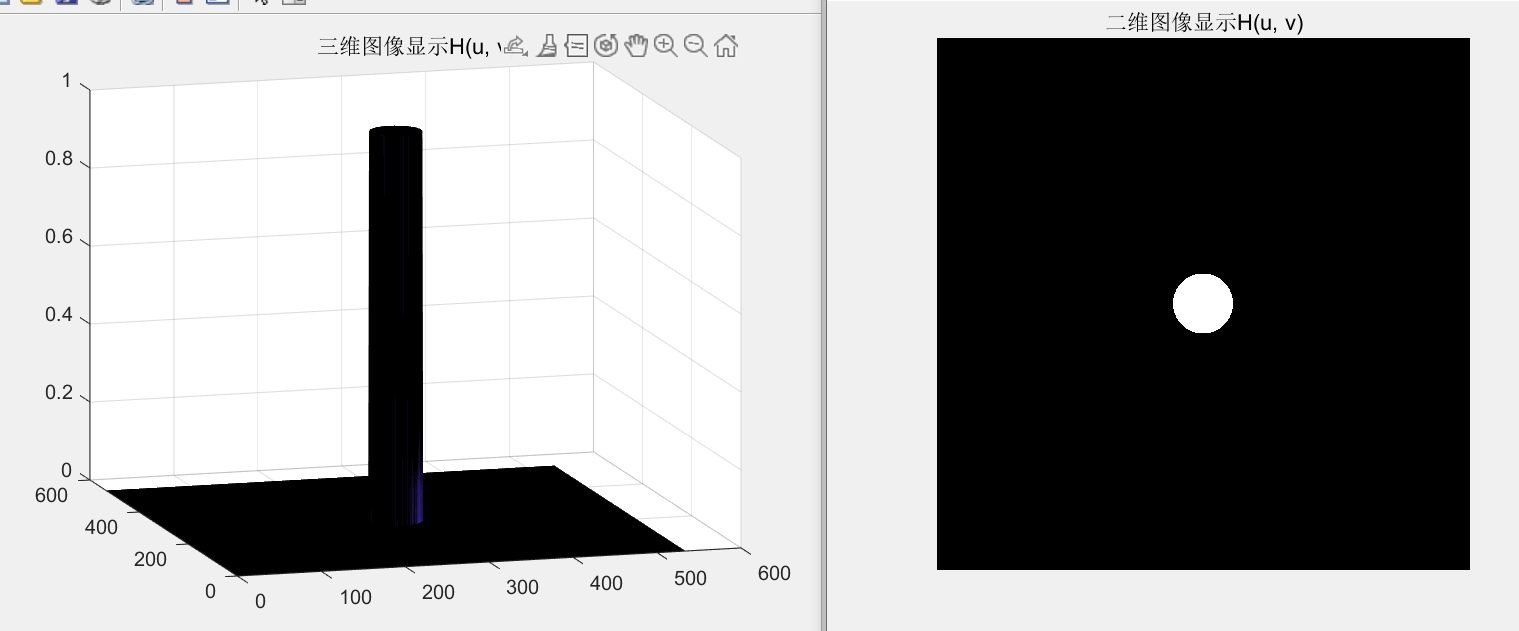
将窗嵌套在幅频上,若是窗越大,涵盖的低频部分更大,高频部分越来越多,即是傅里叶级数越来越大,叠加的越来越多。
当窗口较小时,小级数展开会有较大周期的波动,阶跃处的吉布斯现象产生的波动更易被观察到,随着窗口变大,涵盖的频率从小到大也越来越多,即级数越来越大,波动的周期会变小。
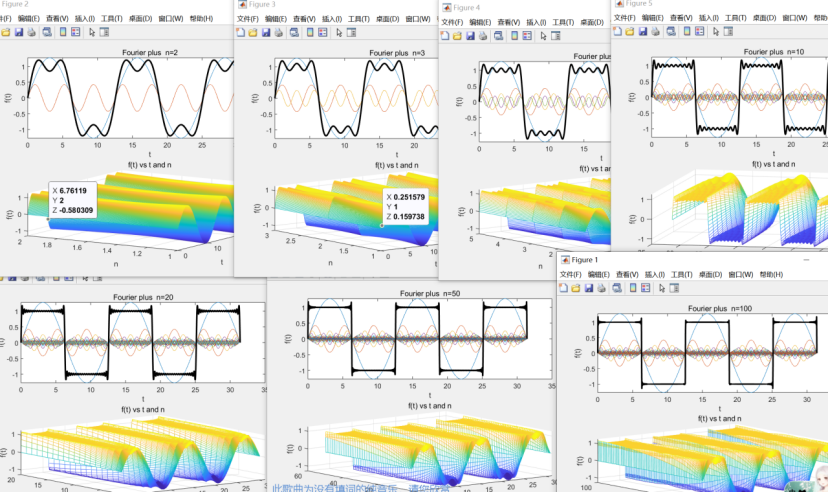
这个从图像中也可以得到,当窗在有明显振铃效应出现时变大,则振铃效应的波纹越发密集。

所以,就可以得到这样的结论:图像的边缘是阶跃信号,完整的幅频对应了大级数的“拟合”,会非常契合原图像,而加上频域滤波之后,相当于只保留了小级数的叠加态,会有明显的吉布斯现象的波动,导致图像出现“振铃现象”,殊途同归。
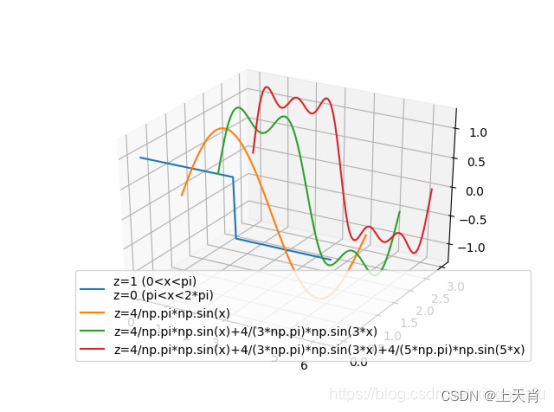
(侵删)

上图来自百度百科
1.2 卷积定理
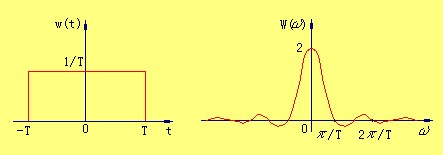
(侵删)
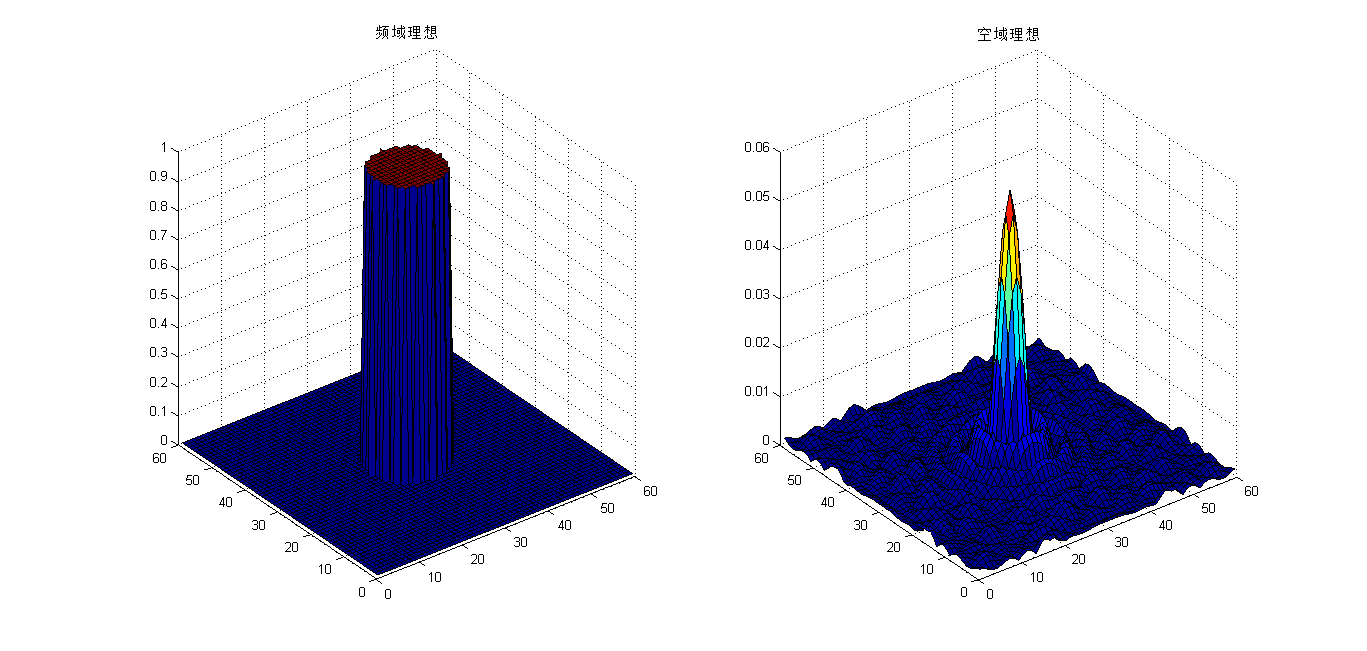
(侵删)
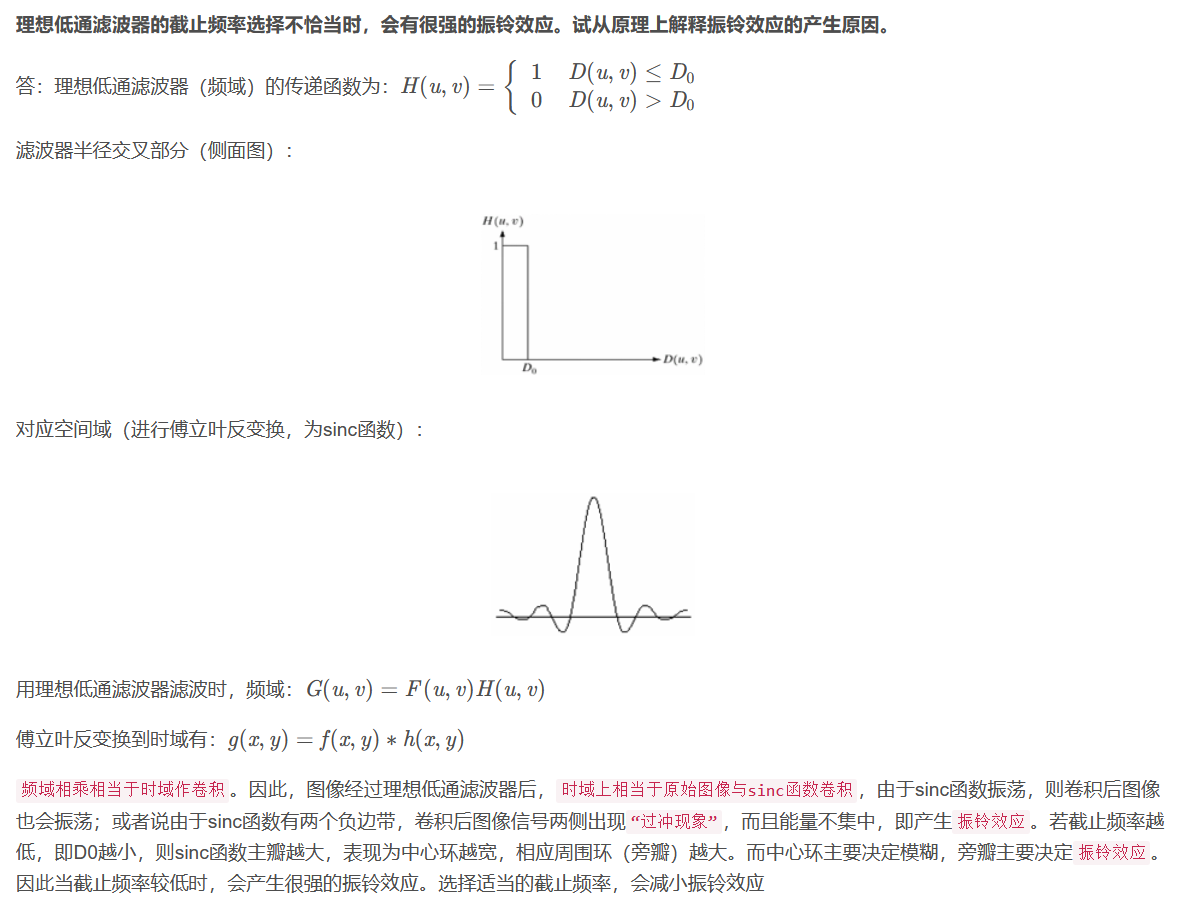
2 振铃效应的消除方法
最常用且最简单的方法便是使用高斯滤波(gaussian filter), 高斯函数的傅里叶变换仍然是高斯函数,故高斯型滤波器不会产生“振铃“。
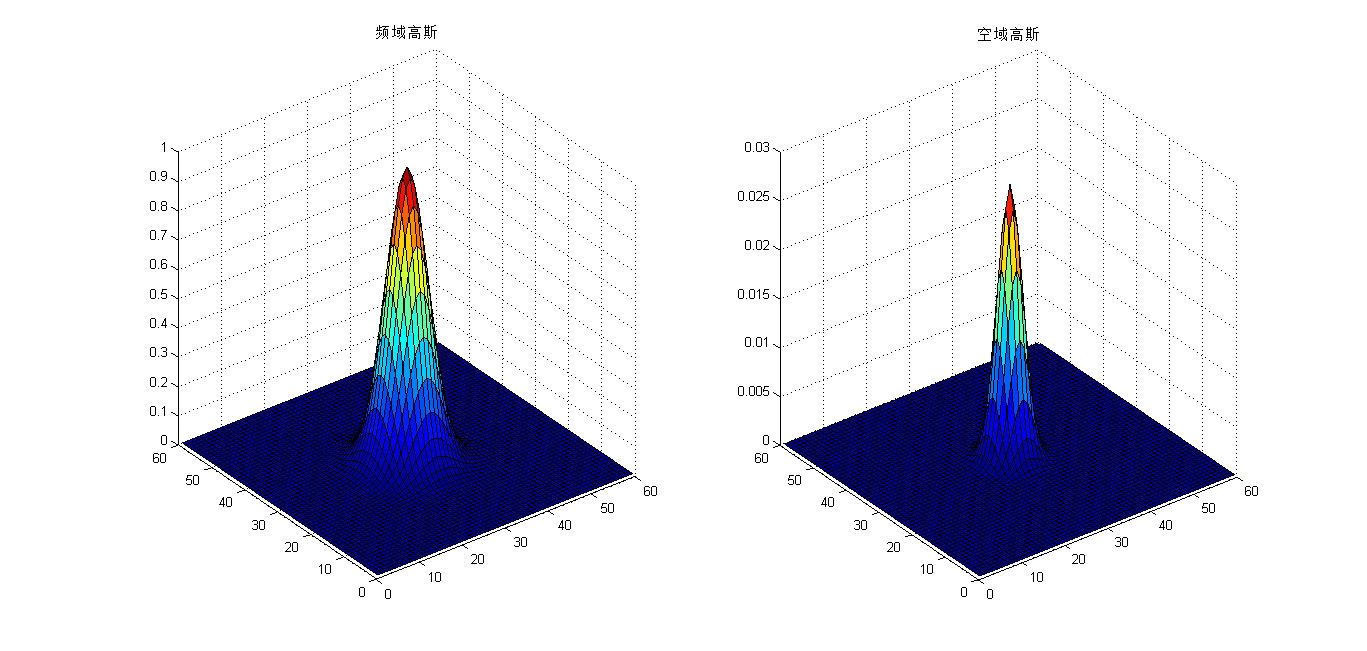
(侵删)
3 启发
- 定量比定性更严谨也更有说服力,但定性分析也会对问题有更直观的感受,更能联结所学、触类旁通
- 学而时习之,将所学常用于实践,才能融会贯通,进而改进和创新





发表评论