【数值计算方法】数值积分&微分-python实现-p3

原文链接：https://www.cnblogs.com/aksoam/p/18332123
更多精彩，关注博客园主页，不断学习！不断进步！

我的主页

csdn很少看私信，有事请b站私信

博客园主页-发文字笔记-常用

有限元鹰的主页 内容：

1. abaqus数值模拟相关
2. python科学计算
3. 开源框架，编程学习笔记

哔哩哔哩主页-发视频-常用

fe-有限元鹰的个人空间 内容：

1. 模拟案例
2. 网格划分
3. 游戏视频，及其他搬运视频

6. 多重积分

本节考虑多重积分的两种计算方法:

• 第一种方法可看成前面几节关于单重积分的推广 ,计算重数较小的积分时有效 .
• 第二种方法称为蒙特卡罗 (monte carlo) 方法 , 是一种随机算法 , 处理高维积分时特别有效

6.1 从一重积分推广到二重积分

以二重积分为例,考虑:

$$i={\iint }_{\omega }f(x,y)\mathrm{d}x\mathrm{d}y,$$

其中,$\omega =a\le x\le b,{\phi }_1(x)\le y\le {\phi }_2(x)$

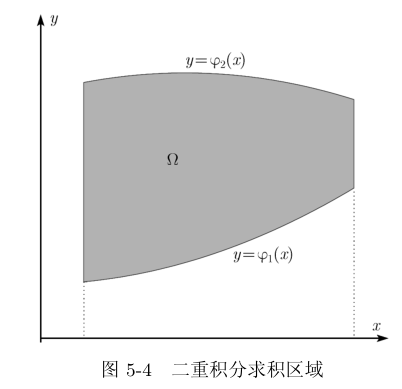
根据二重积分性质:

$$i={\iint }_{\omega }f(x,y)\mathrm{d}x\mathrm{d}y={\int }_a^b\mathrm{d}x{\int }_{{\phi }_1(x)}^{{\phi }_2(x)}f(x,y)\mathrm{d}y.$$

令:

$$f(x)={\int }_{{\phi }_1(x)}^{{\phi }_2(x)}f(x,y)\mathrm{d}y,$$

$$i={\int }_a^{b}f(x)\mathrm{d}x\approx \sum _{i=0}^n{\omega }_i^{(1)}f(x_i).$$

为了求出$f(x_i)$,将区间 $[{\phi }_1(x),{\phi }_2(x)]$ 分为m份. 利用单重积分求积公式得:

$$f(x_i)={\int }_{{\phi }_1(x_i)}^{{\phi }_2(x_i)}f(x_i,y)\mathrm{d}y\approx \sum _{j=0}^m{\omega }_j^{(2)}f(x_i,y_j).$$

${\omega }_i^{(1)}\text{ 和 }{\omega }_j^{(2)}$ 分别是 x 方向和 y 方向的求积系数.记 ${\omega }_{ij}={\omega }_i^{(1)}\cdot {\omega }_j^{(2)}$ ,则有二重积分的求积公式:

$$i={\iint }_{\omega }f(x,y)\mathrm{d}x\mathrm{d}y\approx \sum _{i=0}^n\sum _{j=0}^m{\omega }_{ij}f(x_i,y_j).\text{\hspace{1em}(8)}$$

因此一般来说 , 计算高维数值积分用复合辛普森公式以及前几节介绍的方法都失效.

6.2 蒙特卡罗方法

记 $x_i(i=1,2,\cdot \cdot \cdot ,n)$ 为相互独立的服从区间 [0,1] 上均匀分布的随机变量,则:

$$i_n[f]=\frac{1}{n}\sum _{i=1}^{n}f(x_i).$$

$x_i$ 可通过 n 次独立实验得到 . 由概率论中的大数定理 , 当 n → ∞ 时 , i n [f] 依概率收敛于 f(x)的积分值, 即:

$$i_n[f]\stackrel{\mathrm{p}}{}i[f].$$

可以估计f的方差 $var(f)$ ,取随机变量x的n个样本值 $x_1,x_2,\cdots ,x_n$ ,令:

$${\overline{i}}_n=\frac{1}{n}\sum _{i=1}^{n}f(x_i).$$

then:

$$\mathrm{var}(f)\approx \frac{1}{n}\sum _{i=1}^n(f(x_i)-{\overline{i}}_n{)}^2$$

这个思路推广到高维积分:

$$i={\int }_0^1\cdots {\int }_0^{1}f(x_1,x_2,\cdots ,x_d)\mathrm{d}{x}_1\mathrm{d}{x}_2\cdots \mathrm{d}{x}_d.$$

仍可取 n 次独立样本值的算术平均:

$$i_n[f]=\frac{1}{n}\sum _{i=1}^{n}f(x_1^{(i)},x_2^{(i)},\cdots ,x_d^{(i)})$$

作为多重积分 i 的无偏估计量 , 其方差仍为$\frac{\mathrm{var}(f)}{n}$,收敛速度不受积分区域维数 d 的影响.

• 推广到[a,b]的积分范围

那么,如果计算积分:

$$i={\int }_a^{b}f(x)dx$$

对应的蒙特卡洛积分为

$$i^n=\frac{1}{n}\sum _{i=1}^n\frac{f(x_i)}{pdf(x_i)}$$

其中, $pdf(x_i)$ 是概率密度函数, 它描述了随机变量x的概率分布.之前的x_{u(0,1),pdf(x)=1/(1-0),如果x}u(a,b),则pdf(x)=1/(b-a).

• 积分范围推广到[-inf,+inf]的蒙特卡洛方法

积分:

$$f={\int }_{-\infty }^{+\infty }f(x)\mathrm{d}x.$$

可以看成是服从于正态分布随机变量 x 的函数 h(x) 的数学期望, 通过 n 次独立取样的算术平均近似计算:

$$f\approx f_n=\frac{1}{n}\sum _{i=1}^{n}h(x_i),h(x)=\sqrt{2\pi }{\mathrm{e}}^{\frac{x^2}{2}}f(x).$$

可以证明:$e(f_n)=f$

数值微分

介绍两种近似方法：

• 基于拉格朗日插值多项式的求导方法
• 基于样条函数的求导方法

7.基于拉格朗日插值多项式的求导方法

已知 $f(x)$ 在离散点处的函数值 $f(x_i)(i=1,2,\cdot \cdot \cdot ,n)$, 可以作出 n 次拉格朗日插值多项式 $l_n(x)$ ,再利用 $l_n(x)$ 的导数来近似代替 $f(x)$ 的导数 , 此方法称为基于拉格朗日插值多项式的数值求导方法

插值余项为:

$$r_n(x)=f(x)-l_n(x)=\frac{f^{(n+1)}(\xi )}{(n+1)!}\pi (x),\xi \in (a,b).$$

$$r_n^{\prime }(x)=f^{\prime }(x_i)-l_n^{\prime }(x_i)=\frac{f^{(n+1)}(\xi )}{(n+1)!}{\pi }^{\prime }(x_i)=\frac{f^{(n+1)}(\xi )}{(n+1)!}\prod _{j=0,j\ne i}^n(x_i-x_j).\text{\hspace{1em}(10)}$$

以下是基于等距节点的低阶求导计算公式

两点公式

作 f(x) 的线性插值公式:

$$l_1(x)=\frac{x-x_1}{x_0-x_1}f(x_0)+\frac{x-x_0}{x_1-x_0}f(x_1),$$

求导后,令$x=x_0,x_1-x_0=h,$得:

$$l_1^{\prime }(x_0)=\frac{f(x_1)-f(x_0)}{h}.$$

根据公式(10),余项为 $\frac{f^{\prime \prime }(\xi )}{2}(x_0-x_1)$,即:

$$f^{\prime }(x_0)=\frac{f(x_1)-f(x_0)}{h}-\frac{h}{2}{f}^{\prime \prime }(\xi ),\xi \in (x_0,x_1).\text{\hspace{1em}(11-1)}$$

$$f^{\prime }(x_1)=\frac{f(x_1)-f(x_0)}{h}+\frac{h}{2}{f}^{\prime \prime }(\xi ),\xi \in (x_0,x_1).\text{\hspace{1em}(11-2)}$$

略去余项,(11-1),(11-2)称为计算导数的两点公式.分别是向前差商公式和向后差商公式,精度1阶,误差$o(h)$.

三点及五点公式

作 f(x) 的二次插值多项式:

$$l_2(x)=\frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}f(x_0)+\frac{(x-x_0)(x-x_1)}{(x_1-x_0)(x_1-x_2)}f(x_1)+\frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}f(x_2).$$

令 $x=x_0+th,x_i=x_0+ih,$ 上式变成:

$$l_2(x_0+th)=\frac{1}{2}(t-1)(t-2)f(x_0)-t(t-2)f(x_1)+\frac{1}{2}t(t-1)f(x_2),$$

求导,并令t=0,1,2,得:

$$\begin{array}{rl}& f^{\prime }(x_0)=\frac{1}{2h}[-3f(x_0)+4f(x_1)-f(x_2)]+\frac{h^2}{3}{f}^{(3)}(\xi ),\\ & f^{\prime }(x_1)=\frac{1}{2h}[-f(x_0)+f(x_2)]-\frac{h^2}{6}{f}^{(3)}(\xi ),\\ & f^{\prime }(x_2)=\frac{1}{2h}[f(x_0)-4f(x_1)+3f(x_2)]+\frac{h^2}{3}{f}^{(3)}(\xi ).\end{array}\text{\hspace{1em}(12)}$$

以上是带余项的计算导数的三点公式,精度2阶,误差$o(h^2)$.(12-2)为中心差商公式.

同理,五点求导公式为:

$$\begin{array}{rl}& f^{\prime }(x_0)=\frac{1}{12h}(-25f_0+48f_1-36f_2+16f_3-3f_4)+\frac{h^4}{5}{f}^{(5)}(\xi ),\\ & f^{\prime }(x_1)=\frac{1}{12h}(-3f_0-10f_1+18f_2-6f_3+f_4)-\frac{h^4}{20}{f}^{(5)}(\xi ),\\ & f^{\prime }(x_2)=\frac{1}{12h}(f_0-8f_1+8f_3-f_4)-\frac{h^4}{30}{f}^{(5)}(\xi ),\\ & f^{\prime }(x_3)=\frac{1}{12h}(-f_0+6f_1-18f_2+10f_3+3f_4)-\frac{h^4}{20}{f}^{(5)}(\xi ),\\ & f^{\prime }(x_4)=\frac{1}{12h}(3f_0-16f_1+36f_2-48f_3+25f_4)+\frac{h^4}{5}{f}^{(5)}(\xi ).\end{array}\text{\hspace{1em}(13)}$$

8. 基于样条函数的求导方法

$$\underset{a⩽x⩽b}{\max }|f^{(k)}(x)-s^{(k)}(x)|⩽c{h}^{4-k},k=0,1,2,3,$$

其中,$h={\max }_{0⩽i⩽n-1}{h}_i.$

设$a=x_0<x_1<\cdots <x_n=b,h_i=x_{i+1}-x_i(i=0,1,\cdots ,n-1).$,且样条函数s(x)在$x_i$处的导数为$s^{\prime }(x_i)=m_i$,则在区间$(x_i,x_{i+1})$上,s(x)为三次多项式,即:

$$\begin{array}{c}{s}_i(x)=\frac{h_i+2(x-x_i)}{h_i^3}(x-x_{i+1}{)}^2{f}_i+\frac{h_i-2(x-x_{i+1})}{h_i^3}(x-x_i{)}^2{f}_{i+1}\\ +\frac{(x-x_i)(x-x_{i+1}{)}^2}{h_i^2}{m}_i+\frac{(x-x_{i+1})(x-x_{i+1}{)}^2}{h_i^2}{m}_{i+1}.\end{array}\text{\hspace{1em}(14)}$$

想要求出$m_i(i=0,1,\cdots ,n)$.需要$s^{\prime \prime }(x)$在$x_i$处连续以及边界条件.

1. 若$s^{\prime }(x_0)=f_0^{\prime }=m_0,s^{\prime }(x_n)=f_n^{\prime }=m_n$已知.m_i满足方程组:

上述方程组 (5.62), (5.65), (5.66) 称为三转角方程组 . 可用追赶法进行求解 . 再将计算结果代入式 (5.61) 中便得 s(x) 以及 s(x) 在任意点 x 处的导数值

由于上述求导数的方法需要求解线性方程组 , 因此也称为隐式格式 . 它具有数值计算稳定的特点 , 可以求出任意点 ( 不一定为节点 ) 的导数值 , 而且精度较高 .

数值实验

# 数值实验t1
from formu_lib import *
def com3pgausslengendre(f,a:float,b:float,n:int):
    # 复合三点高斯-勒让德计算积分
    x=[a+i*(b-a)/n for i in range(n+1)]
    return sum([integ1dguasslegendre(f,x[i],x[i+1],3)for i in range(n)])

# 积分函数
pi=lambda x: 4/(1+x**2)

# 积分范围
a,b=0,1

# 复合simpson计算积分
r1=varstepinteg1d(pi,a,b,1e-8,method=3)

r2=com3pgausslengendre(pi,a,b,100)
showerror(r1,np.pi)
showerror(r2,np.pi)
# 数值解: 3.1415926535528365, 精确解: 3.141592653589793, 误差: 1.1763670223853885e-11
# 数值解: 3.1415926535897927, 精确解: 3.141592653589793, 误差: 1.4135798584282297e-16

# t2
from formu_lib import *

# 积分函数
f=lambda x: np.sqrt(4-np.sin(x)**2)
a,b=0,np.pi/4

r1=varstepinteg1d(f,a,b,1e-6,method=3)
showerror(r1,1.53439197)
# 数值解: 1.5343920054108953, 精确解: 1.53439197, 误差: -2.3078128678621626e-08

求解代码:

from formu_lib import *

# 积分函数
f8=lambda x: 1/(1+x**2)
a,b=-5,5

result=[]
accurateval=[]
ns=[]
for n in range(1,51):
    result.append(integ1dnewtoncotes(f8,a,b,n))
    ns.append(n)
    accurateval.append(2*np.arctan(5))

from matplotlib import pyplot as plt
plt.plot(ns,result,label='numerical solution')
plt.plot(ns,accurateval,label='accurate solution')
plt.xlabel('newton-cotes points number')
plt.ylabel(' integrate value')
plt.title('newton-cotes integration value vs points number')
plt.show()

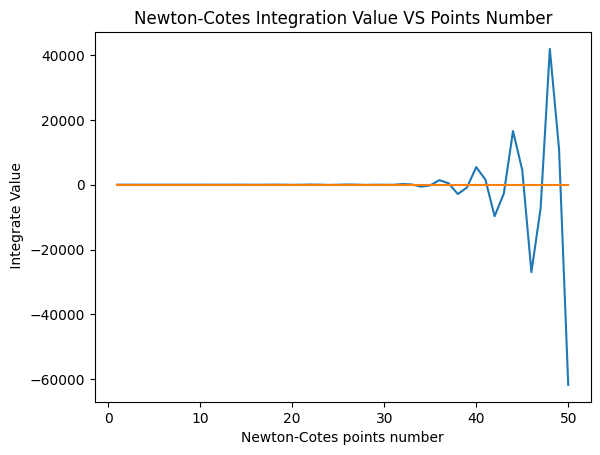
从上图可以看出,当随着n的增加, 牛顿-科特斯积分的逐渐不稳定, 但误差也越来越大.不收敛.

code:

# t4
from formu_lib import *
x=[1900,1910,1920,1930,1940,1950,1960,1970,1980,1990]
fs=[76.0,92.0,106.5,123.2,131.7,150.7,179.3,204.0,226.5,251.4]

df1=diff1dforward(x,fs)
df2=diff1dbackward(x,fs)
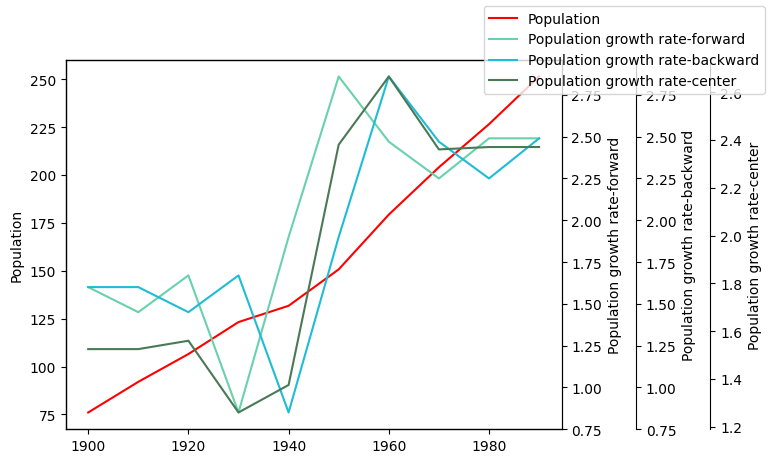
df3=diff1dcentral(x,fs)
plotlines([x,x[:],x[:],x],[fs,df1,df2,df3],["population","population growth rate-forward","population growth rate-backward","population growth rate-center"])

资料:显式和隐式方法 - 维基百科，自由的百科全书

取步长为h,则: $x_i=a+ih,i=0,1,2,...,n,h=\frac{b-a}{n},x_{i+1}-x_i=h.$ 使用向前差商公式,则有:

$$y^{\prime }(x_i)=\frac{y(x_{i+1})-y(x_i)}{h}$$

代入方程后:

$$y(x_{i+1})-y(x_i)=hf[x_i,y(x_i)],$$

$$y(x_{i+1})=y(x_i)+hf[x_i,y(x_i)],$$

这是显式格式.

如果使用向后差商公式,则有:

$$y^{\prime }(x_{i+1})=\frac{y(x_{i+1})-y(x_i)}{h}$$

代入方程后:

$$y(x_{i+1})-y(x_i)=hf[x_{i+1},y(x_{i+1})],$$

$$y(x_{i+1})-hf[x_{i+1},y(x_{i+1})]=y(x_i)$$

这是隐式格式

• 验证

取$f(x,y)=-y^2,a=0,y(0)=1,b=5>x>a,n取值为100$,则:

# t6
from formu_lib import *
import numpy as np
a,b,n=0,5,100
h=(b-a)/n
x=[a+i*h for i in range(n+1)]

f=lambda x: -x*x

# result var
ye,yi=np.zeros(n+1),np.zeros(n+1)
ye[0],yi[0]=1,1

# explicit method
for i in range(n):
    ye[i+1]=ye[i]+h*f(ye[i])

# implicit method
for i in range(n):
    yi[i+1]=(-1-np.sqrt(1+4*h*yi[i]))/(2*h)

plotlines([x,x],[ye,yi],["y(x)-explictsol","y(x)-implicitsol"])

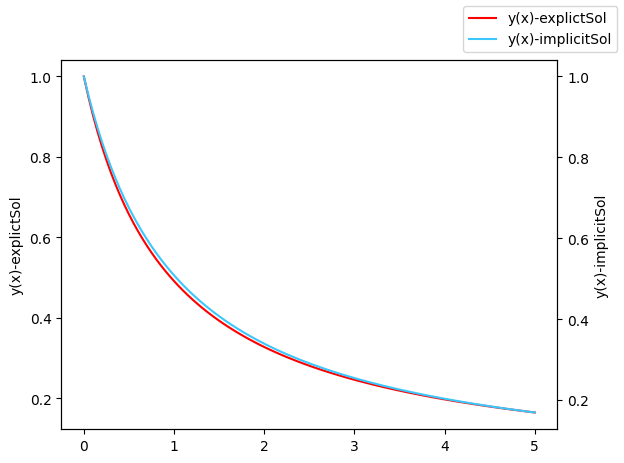
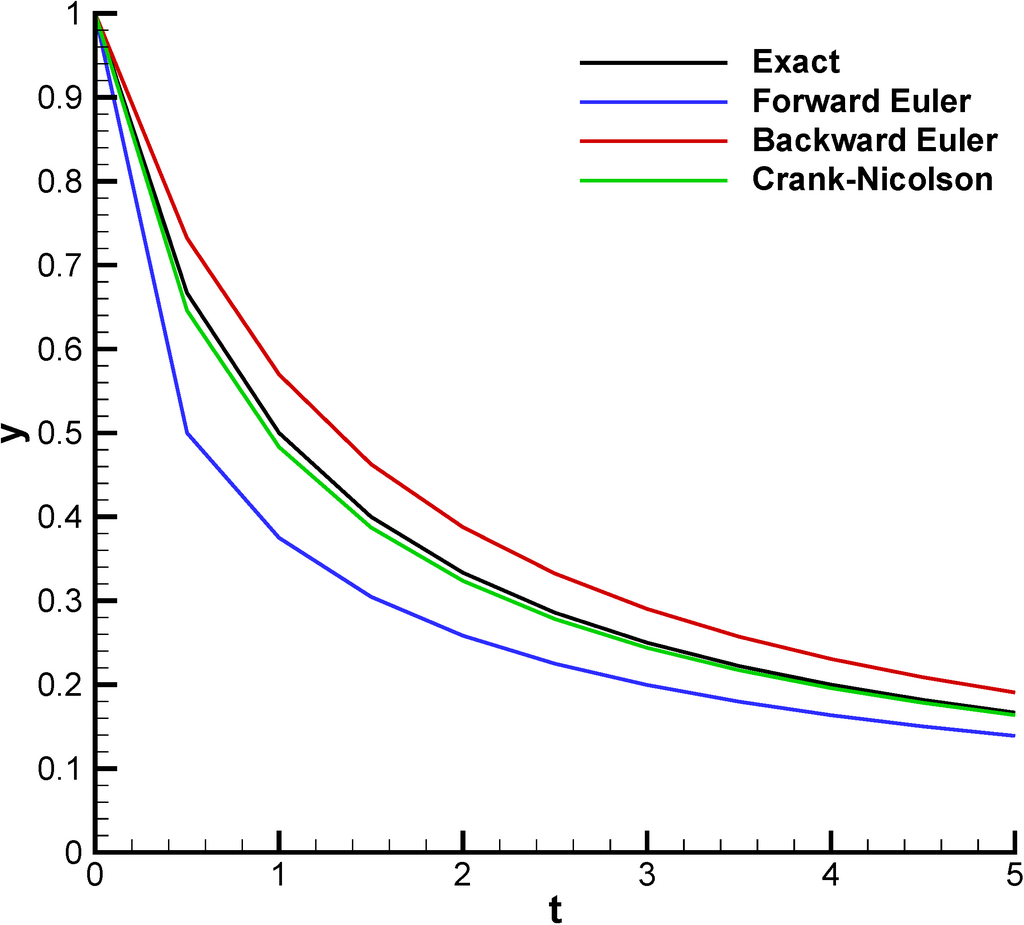
精确结果: