文章目录
1.图简介
在数学中,图是描述于一组对象的结构,其中某些对象对在某种意义上是“相关的”。这些对象对应于称为顶点的数学抽象(也称为节点或点),并且每个相关的顶点对都称为边(也称为链接或线)。通常,图形以图解形式描绘为顶点的一组点或环,并通过边的线或曲线连接。 图形是离散数学的研究对象之一。
图的类型分为单向图和双向图,其中双向图中有个变种叫做加权(优先级)图:
- 单向图: 例如城市里的单行路里面只能走一个方向不能掉头往回走的马路。
- 无向图:例如城市里随处可见包含了正反两个方向的马路,这种路可以掉头。
- 带权图: 例如使用导航的时候,距离最短并不说明这条路线是最优路线,因为可能会堵车。这时候,带权图就可以帮助我们解决问题。
单向图如下图所示,箭头标识每个顶点之间的关系,如果需要关联双向关系的话,以a为例则需要添加c与a关联的箭头。
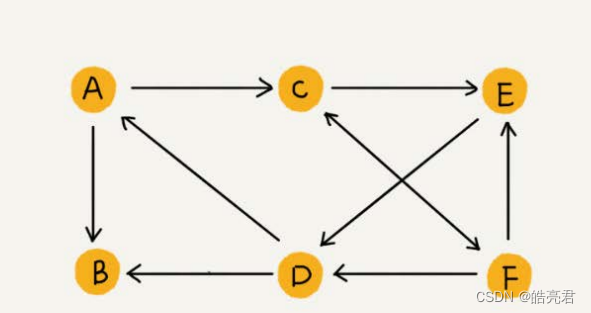
双向图如下图所示,顶点相邻的线没有箭头,表示是一个双向的关系。
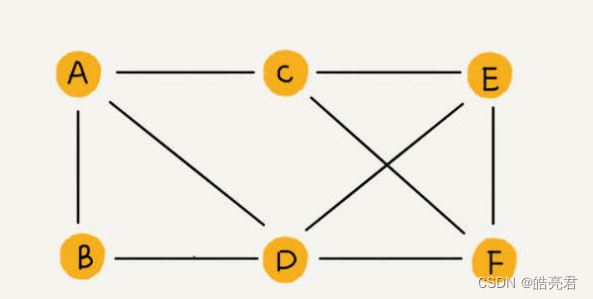
带权图如下图所示,两个顶点之间连接线上的数值标识权重值,可以根据权重值升序或降序优先找最优路径。
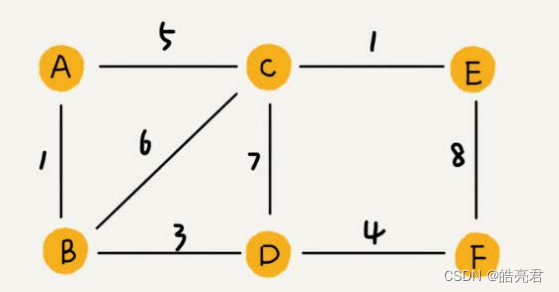
2.图的存储方式
2.1.邻接矩阵存储方法
图最直观的一种存储方法就是,邻接矩阵(adjacency matrix)。邻接矩阵的底层依赖一个二维数组。对于无向图来说,如果顶点i与顶点j之间有边,我们就将a[i][j]和a[j][i]标记为1;对于有向图来说,如果顶点i到顶点j之间,有一条箭头从顶点i指向顶点j的边,那我们就将a[i][j]标记为1。同理,如果有一条箭头从顶点j指向顶点i的边,我们就将a[j][i]标记为1。对于带权图,数组中就存储相应的权重。
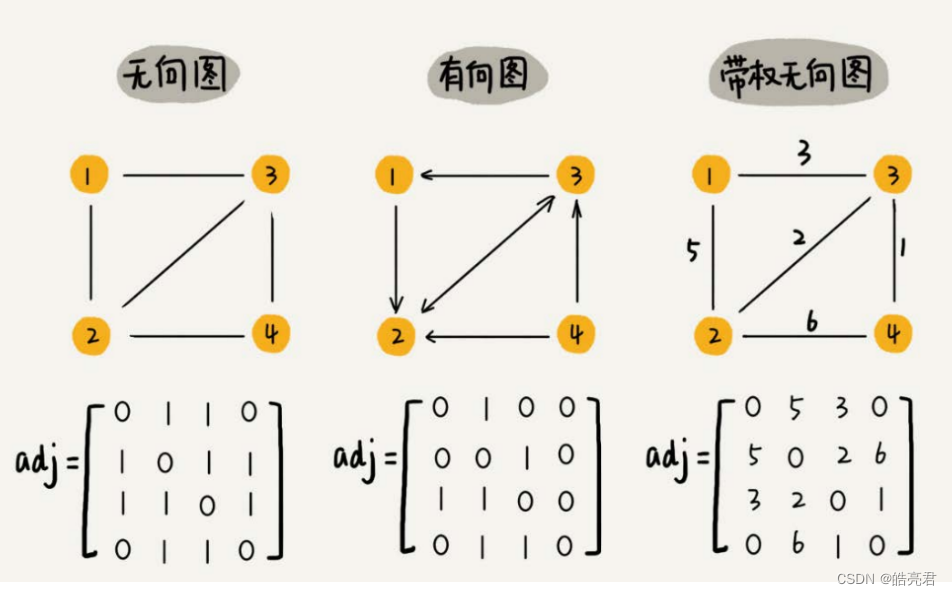
用邻接矩阵来表示一个图,虽然简单、直观,但是比较浪费存储空间。为什么这么说呢?
对于无向图来说,如果a[i][j]等于1,那a[j][i]也肯定等于1。实际上,我们只需要存储一个就可以了。也就是说,无向图的二维数组中,如果我们将其用对角线划分为上下两部分,那我们只需要利用上面或者下面这样一半的空间就足够了,另外一半白白浪费掉了。
2.2.邻接表存储方法
针对2.1.邻接矩阵比较浪费内存空间的问题可以使用邻接表(adjacency list)解决。邻接表有点像散列表,每个顶点对应一条链表,链表中存储的是与这个顶点相连接的其他顶点。下图是有向图的邻接表存储方式,每个顶点对应的链表里面,存储的是指向的顶点。对于无向图来说,也是类似的。
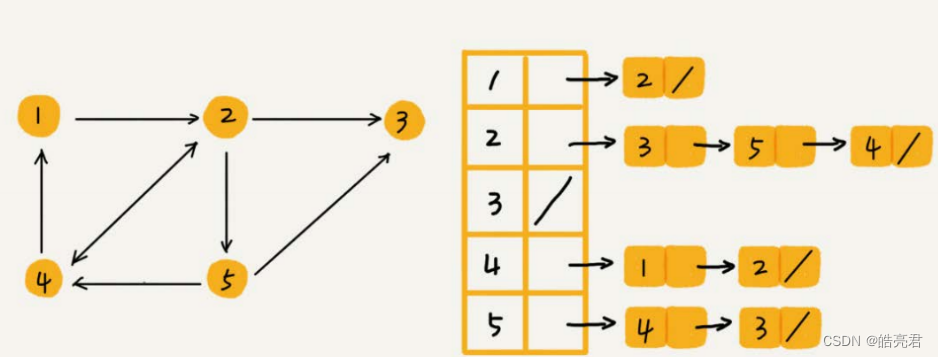
3.有向、无向图和查询算法
3.1.数据结构
本文以邻接表的方式实现图的存储,感兴趣的自己可以用邻接矩阵实现。
@data
public class graph {
/**
* 顶点的个数
*/
private int size;
/**
* 邻接表
*/
private linkedlist<integer> tables[];
/**
* 深度优先找到路径标识
*/
private boolean found = false;
public graph(int size) {
this.size = size;
tables = new linkedlist[size];
for (int i = 0; i < size; i++) {
tables[i] = new linkedlist<>();
}
}
/**
* 无向图一条边存两次
*
* @param v 顶点v
* @param e 边集e
*/
public void addedge(int v, int e) {
if (v > size) {
return;
}
tables[v].add(e);
//注释下面一行就是单向图
tables[e].add(v);
}
/**
* 递归打印s->t的路径
*/
private void print(int[] prev, int s, int t) {
if (prev[t] != -1 && t != s) {
print(prev, s, prev[t]);
}
system.out.print(t + " ");
}
}
在上面代码中把addedge()函数中的 tables[e].add(v); 注释掉了话,无向图就成了单向图。
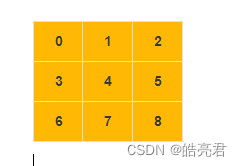
以上图数据为例,把二维数组中数据转换成图中的代码 如下
public static void main(string[] args) {
graph graph = new graph(9);
int[][] nums = new int[][]{{0, 1, 2}, {3, 4, 5}, {6, 7, 8}};
int rowlen = nums.length;
int collen = nums[0].length;
for (int i = 0; i < rowlen; i++) {
for (int j = 0; j < collen; j++) {
if (j < collen - 1) {
//将相下一列的数值加到边中
graph.addedge(nums[i][j], nums[i][j + 1]);
}
if (i < rowlen - 1) {
//将相邻下一行的数值加到边中
graph.addedge(nums[i][j], nums[i + 1][j]);
}
}
}
system.out.println(jsonobject.tojsonstring(graph));
运行结果如下,可以看出每个顶点都把相邻的边数据存放到链表中了
{"found":false,"size":9,"tables":[[1,3],[0,2,4],[1,5],[0,4,6],[1,3,5,7],[2,4,8],[3,7],[4,6,8],[5,7]]}
把addedge()函数中的 tables[e].add(v); 注释掉了测试返回结果如下
{"found":false,"size":9,"tables":[[1,3],[2,4],[5],[4,6],[5,7],[8],[7],[8],[]]}
3.2.广度优先算法bfs
广度优先搜索(breadth-first-search),我们平常都把简称为bfs。直观地讲,它其实就是一种“地毯式”层层推进的搜索策略,即先查找离起始顶点最近的,然后是次近的,依次往外搜索。理解起来并不难,以下以顶0点到顶8点为例找寻最短路径过程。

上图先从 [1,3]开始查找,途径[2,4,6],[5,7]最后找到8,最优路径为下图,0->1->2->5->8 加起来的步数为16位最低,广度优先搜索算法有点类于动态规划算法都是获取全局最优解。
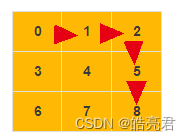
以3.1的数据结构为例实现广度优先搜索
/**
* 广度优先查询算法
*
* @param start 起点
* @param end 终点
*/
public void bfs(int start, int end) {
if (start == end) return;
boolean[] visited = new boolean[size];
//是用来记录已经被访问的顶点,用来避免顶点被重复访问。如果顶点s被访问,那相应的visited[s]会被设置为true。
visited[start] = true;
/*
用来存储已经被访问、但相连的顶点还没有被访问的顶点。因为广度优先搜索是逐层访问的,也就是说,我们只有把第k层的顶点都访问完成
之后,才能访问第k+1层的顶点。当我们访问到第k层的顶点的时候,我们需要把第k层的顶点记录下来,稍后才能通过第k层的顶点来找第k+1层的顶点。所以,我
们用这个队列来实现记录的功能。
*/
queue<integer> queue = new linkedlist<>();
queue.add(start);
/*
用来记录搜索路径。当我们从顶点s开始,广度优先搜索到顶点t后,prev数组中存储的就是搜索的路径。不过,这个路径是反向存储的。prev[w]存储的是,顶
点w是从哪个前驱顶点遍历过来的。比如,我们通过顶点2的邻接表访问到顶点3,那prev[3]就等于2。为了正向打印出路径,我们需要递归地来打印,你可以看
下print()函数的实现方式。
*/
int[] prev = new int[size];
for (int i = 0; i < size; ++i) {
prev[i] = -1;
}
//循环停止条件 队列大小为0
while (queue.size() != 0) {
//从队列里取出一条数据
int w = queue.poll();
//遍历次数等于链表的长度
for (int i = 0; i < tables[w].size(); ++i) {
//从链表中取出相邻边值
int q = tables[w].get(i);
//如果没有被访问
if (!visited[q]) {
//记录搜索路径的值
prev[q] = w;
//找到了值打印数据并结束循环
if (q == end) {
print(prev, start, end);
return;
}
//设置当前节点q为访问过
visited[q] = true;
//设置当前边值到队列中
queue.add(q);
}
}
}
}
测试广度优先搜索
public static void main(string[] args) {
graph graph = new graph(9);
int[][] nums = new int[][]{{0, 1, 2}, {3, 4, 5}, {6, 7, 8}};
int rowlen = nums.length;
int collen = nums[0].length;
for (int i = 0; i < rowlen; i++) {
for (int j = 0; j < collen; j++) {
if (j < collen - 1) {
graph.addedge(nums[i][j], nums[i][j + 1]);
}
if (i < rowlen - 1) {
graph.addedge(nums[i][j], nums[i + 1][j]);
}
}
}
//广度优先搜索
graph.bfs(0, 8);

3.3.深度优先算法dfs
深度优先搜索(depth-first-search),简称dfs。最直观的例子就是“走迷宫”。假设你站在迷宫的某个岔路口,然后想找到出口。你随意选择一个岔路口来走,走着走着发现走不通的时候,你就回退到上一个岔路口,重新选择一条路继续走,直到最终找到出口。这种走法就是一种深度优先搜索策略。走迷宫的例子很容易能看懂,我们现在再来看下,如何在图中应用深度优先搜索,来找某个顶点到另一个顶点的路径,以顶点0到右下角顶点8为例,从0->1->2->5->4->3->6->7->8

3.3.1.dfs查询单条路径
以3.1的数据结构为例实现深度优先搜索
/**
* 深度优先查询算法
* @param start 起点
* @param end 终点
*/
public void dfs(int start, int end) {
found = false;
//访问过的标识
boolean[] visited = new boolean[size];
//记录搜索过的路径
int[] prev = new int[size];
for (int i = 0; i < size; ++i) {
prev[i] = -1;
}
recurdfs(start, end, visited, prev);
print(prev, start, end);
found = false;
}
/**
* 递归搜索
*
* @param start 起点
* @param end 终点
* @param visited 已访问标识
* @param prev 搜索路径
*/
private void recurdfs(int start, int end, boolean[] visited, int[] prev) {
if (found == true) return;
//设置节点访问过
visited[start] = true;
//如果出发和结束地点一样则停止循环
if (start == end) {
found = true;
return;
}
for(integer nextnode: tables[start]){
//如果当前节点未被访问,则尝试使用
if (!visited[nextnode]) {
prev[nextnode] = start;
//以找到的相邻点的位置作为递归的下一项
recurdfs(nextnode, end, visited, prev);
}
}
}
将3.2章节测试广度优先的代码里把调用graph.bfs(0, 8)改成graph.dfs(0, 8) 后运行结果如下

3.3.2.dfs查询所有路径
以3.1的数据结构为例实现深度优先搜索
/**
* 查找
*
* @param start 起点
* @param end 终点
* @return 所有路径
*/
public list<list<integer>> dfsall(int start, int end) {
list<list<integer>> prevlist = new arraylist<>();
//访问过的标识
boolean[] visited = new boolean[size];
list<integer> prev = new arraylist<>();
//添加起点
prev.add(start);
recurdfs(start, end, visited, prev, prevlist);
return prevlist;
}
/**
* @param start 起点
* @param end 终点
* @param visited 已访问标识
* @param prev 路径
* @param prevlist 存放所有匹配路径
*/
private void recurdfs(int start, int end, boolean[] visited, list<integer> prev, list<list<integer>> prevlist) {
//设置当前节点已访问
visited[start] = true;
for (int nextnode : tables[start]) {
//已访问的节点则不进行出路
if (!visited[nextnode]) {
//把节点添加到路径中
prev.add(nextnode);
if (nextnode == end) {
//到达终点后把当前的路径添加到所有路径中
prevlist.add(new arraylist<>(prev));
} else {
//没找到则递归往深处查找
recurdfs(nextnode, end, visited, prev, prevlist);
//递归查找完设置当前节点为未访问
visited[nextnode] = false;
}
//移除最后一位元素
prev.remove(prev.size() - 1);
}
}
}
将3.2章节测试广度优先的代码里把调用graph.bfs(0, 8)以下两行代码,运行结果如下图
list<list<integer>> all = graph.dfsall(0, 8);
system.out.println(jsonobject.tojsonstring(all));

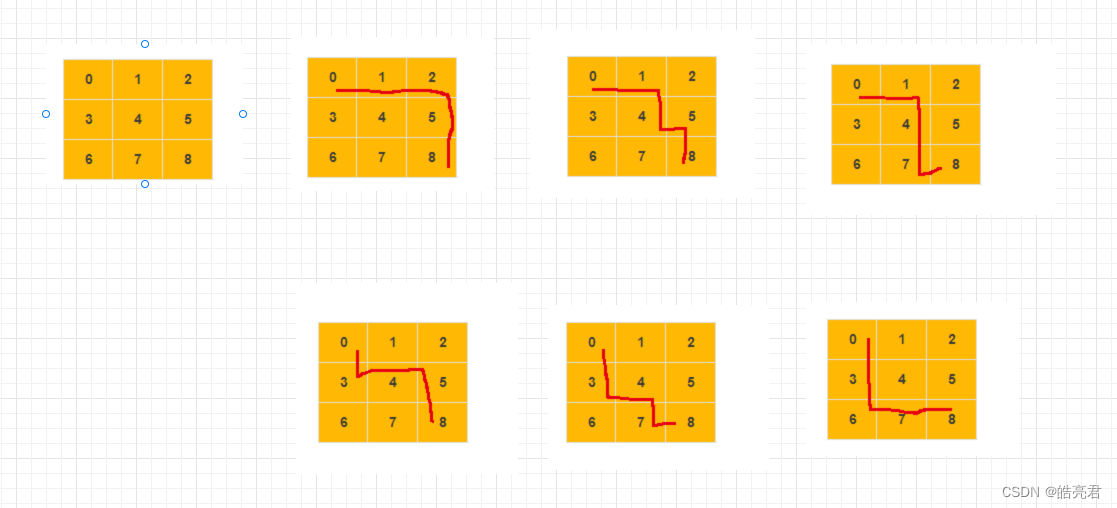
总结:
广度优先搜索和深度优先搜索是图上的两种最常用、最基本的搜索算法,比起其他高级的搜索算法,比如a*、ida*等,要简单粗暴,没有什么优化,所以,也被叫作暴力搜索算法。所以,这两种搜索算法仅适用于状态空间不大,也就是说图不大的搜索。广度优先搜索: 地毯式层层推进,从起始顶点开始,依次往外遍历。广度优先搜索需要借助队列来实现,遍历得到的路径就是,起始顶点到终止顶点的最短路径。深度优先搜索: 回溯思想,非常适合用递归实现。换种说法,深度优先搜索是借助栈来实现的。- 在执行效率方面,
深度优先和广度优先搜索的时间复杂度都是o(e边数),空间复杂度是o(v顶点数)。
4.带权图和贪心算法
4.1.贪心算法
贪心算法(greedy algorithm 又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,算法得到的是在某种意义上的局部最优解。
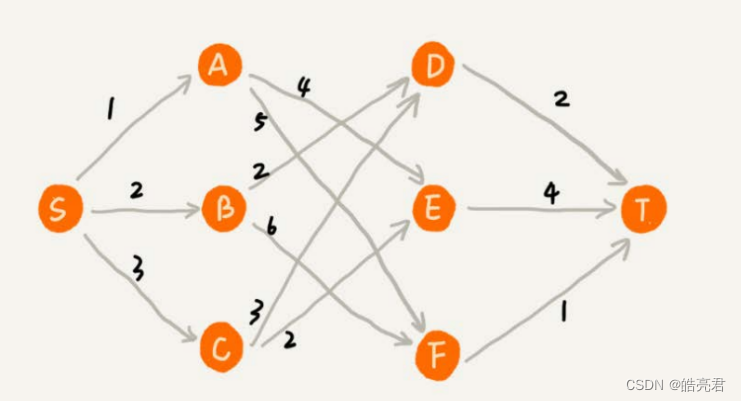
用贪心算法解决问题的思路,并不总能给出最优解。以上图一个带权图中,我们从顶点s开始,找一条到顶点t的最短路径(路径中边的权值和最小)。贪心算法的解决思路是,每次都选择一条跟当前顶点相连的权最小的边,直到找到顶点t。按照这种思路,我们求出的最短路径是s->a->e->t,路径长度是1+4+4=9。
这种贪心的选择方式,最终求的路径并不是最短路径(动态规划算法);因为路径s->b->d->t才是最短路径(路径的长度是2+2+2=6)。贪心算法会前面的选择,会影响后面的选择。
4.2.基于带权无向图使用贪心算法查询最优路径
下图以java代码实现了带权无向图
public class weightedgraph {
/**
* 顶点总数
*/
private final int size;
/**
* 边的总数
*/
private int count;
/**
* 邻接表
*/
private queue<edge>[] queues;
/**
* 创建一个含有size个顶点的空加权无向图
*
* @param size
*/
public weightedgraph(int size) {
//初始化顶点数量
this.size = size;
//初始化边的数量
this.count = 0;
//初始化邻接表
this.queues = new queue[size];
for (int i = 0; i < queues.length; i++) {
queues[i] = new arraydeque<>();
}
}
/**
* 向加权无向图中添加一条边e
*
* @param e
*/
public void addedge(edge e) {
//需要让边e同时出现在e这个边的两个顶点的邻接表中
int v = e.v;
int w = e.other(v);
queues[v].add(e);
queues[w].add(e);
//边的数量+1
count++;
}
/**
* 获取和顶点v关联的所有边
*
* @param index
* @return
*/
public queue<edge> get(int index) {
return queues[index];
}
public static class edge implements comparable<edge> {
/**
* 顶点v
*/
private final int v;
/**
* 顶点w
*/
private final int w;
/**
* 当前边的权重
*/
private final int weight;
/**
* 通过顶点v和w,以及权重weight值构造一个边对象
*
* @param v
* @param w
* @param weight 权重值
*/
public edge(int v, int w, int weight) {
this.v = v;
this.w = w;
this.weight = weight;
}
/**
* 获取边的权重值
*
* @return
*/
public int weight() {
return weight;
}
/**
* 获取边上除了顶点vertex外的另外一个顶点
*
* @return
*/
public int other(int vertex) {
if (vertex == v) {
return w;
} else {
return v;
}
}
@override
public int compareto(edge that) {
//使用一个遍历记录比较的结果
int cmp;
if (this.weight() > that.weight()) {
//如果当前边的权重值大,则让cmp=1;
cmp = 1;
} else if (this.weight() < that.weight()) {
//如果当前边的权重值小,则让cmp=-1;
cmp = -1;
} else {
//如果当前边的权重值和that边的权重值一样大,则让cmp=0
cmp = 0;
}
return cmp;
}
}
}
基于上面邻接表结构的带权图使用贪心算法查找最优路径
/**
* 根据权重数值低的查询两点之间的最优路径
* @param start 起点
* @param end 终点
* @return
*/
public list<integer> searchbyweight(int start, int end) {
if (start >= count || end >= count) {
return null;
}
//记录途径滤镜
list<integer> pathlist = new arraylist<>();
pathlist.add(start);
//获取起点的所有邻边
queue<edge> edges = queues[start];
edge edge;
//是用来记录已经被访问的顶点,用来避免顶点被重复访问。如果顶点q被访问,那相应的visited[last]会被设置为true。
boolean[] visited = new boolean[size];
int last = start;
while (edges != null) {
final int finallast = last;
//过滤掉已经访问过的节点过滤掉并且不能往回走然后获取权重值最小的路径
edge = edges.stream()
.filter(e -> !visited[e.other(finallast)] && e.other(finallast) > finallast)
.min(edge::compareto).get();
visited[last] = true;
last = edge.other(last);
pathlist.add(last);
//找到路径则推出循环
if (last == end) {
break;
}
//继续往下查找
edges = queues[last];
}
return pathlist;
}
上图最难理解的代码段为下面这段,其实分段看就很简单
- 先从所有边里面通过
filter函数过滤掉已访问过的节点和比上一节点值更小(避免走回头路) - 然后通过
min函数找到权重值最小的一条边
edge = edges.stream()
.filter(e -> !visited[e.other(finallast)] && e.other(finallast) > finallast)
.min(edge::compareto).get();
如果是把addedge函数第四行注释掉把无向图改成单向图则不需要上面过滤代码了
edge = edges.stream().min(edge::compareto).get();
测试带权图
- 使用
bimap(双休map)给每个顶点取一个对应的下标值用于在图中存储对应边 - 初始化顶点和边的映射信息和权重值
- 通过贪心算法实现的查询函数查找最优路径的数值后通过bimap获取数值的顶点名称并打印
bimap需要引入第三方依赖,我使用的是hutool工具包,也可以使用guava工具包下的bimap
<dependency>
<groupid>cn.hutool</groupid>
<artifactid>hutool-core</artifactid>
<version>5.8.9</version>
</dependency>
public static void main(string[] args) {
//s=0 a=1 b=2 c=3 d=4 e=5 f=6 t=7
bimap<string, integer> bimap = new bimap<>(new hashmap<>());
bimap.put("s", 0);
bimap.put("a", 1);
bimap.put("b", 2);
bimap.put("c", 3);
bimap.put("d", 4);
bimap.put("e", 5);
bimap.put("f", 6);
bimap.put("t", 7);
weightedgraph weightedgraph = new weightedgraph(8);
//添加顶点s到顶点 a,b,c的映射和权重
weightedgraph.addedge(new weightedgraph.edge(0, 1, 1));
weightedgraph.addedge(new weightedgraph.edge(0, 2, 2));
weightedgraph.addedge(new weightedgraph.edge(0, 3, 3));
//添加顶点a到e,f的映射和权重
weightedgraph.addedge(new weightedgraph.edge(1, 5, 4));
weightedgraph.addedge(new weightedgraph.edge(1, 6, 5));
//添加顶点b到d,f的映射和权重
weightedgraph.addedge(new weightedgraph.edge(2, 4, 2));
weightedgraph.addedge(new weightedgraph.edge(2, 6, 6));
//添加顶点b到d,f的映射和权重
weightedgraph.addedge(new weightedgraph.edge(3, 4, 3));
weightedgraph.addedge(new weightedgraph.edge(3, 5, 2));
weightedgraph.addedge(new weightedgraph.edge(4, 7, 2));
weightedgraph.addedge(new weightedgraph.edge(5, 7, 4));
weightedgraph.addedge(new weightedgraph.edge(6, 7, 1));
list<integer> pathlist = weightedgraph.searchbyweight(0, 7);
stringbuilder sb = new stringbuilder();
for (integer path : pathlist) {
sb.append(bimap.getkey(path)).append("->");
}
sb.deletecharat(sb.length() - 1);
sb.deletecharat(sb.length() - 1);
system.out.println(sb);
}
运行结果如下,可以看到上4.1.章节中带权图样例中最优路径是一致的。



发表评论