▶《强化学习的数学原理》(2024春)_西湖大学赵世钰 Ch4 值迭代 与 策略迭代 【动态规划 model-based】

学堂在线 课程页面链接
中国大学mooc 课程页面链接
b 站 视频链接

ppt和书籍下载网址： 【github 链接】

---

总述：

开始介绍第一个可以找到最优策略的算法。 ——> 动态规划算法

介绍 3 种 迭代算法：
1、值迭代算法： 上一章讨论的求解 bellman 最优方程的压缩映射定理 所提出的算法。
2、策略迭代算法
3、截断策略迭代算法： 值迭代 和 策略迭代 算法是该算法的极端情况。

动态规划 算法，需要系统模型。
本章介绍的策略迭代算法 扩展得到 第 5 章介绍的蒙特卡洛算法。
——————————————
model-based 算法

值迭代 上一章 的延伸
策略迭代 下一章 蒙特卡洛学习的基础

值迭代 和 策略迭代 是 截断策略迭代 的两个极端情况

4.1 值迭代

贝尔曼最优公式 的 矩阵向量形式：

$\mathbf{v}=f(\mathbf{v})=\underset{\pi }{\max }({\mathbf{r}}_{\pi }+\gamma {\mathbf{p}}_{\pi }\mathbf{v})$

求解方法： 上一章 的 压缩映射定理 建议的迭代算法 【值迭代】

${\mathbf{v}}_{k+1}=f({\mathbf{v}}_k)=\underset{\pi }{\max }({\mathbf{r}}_{\pi }+\gamma {\mathbf{p}}_{\pi }{\mathbf{v}}_k),k=1,2,\mathrm{3...}$

其中 ${\mathbf{v}}_0$ 可为任意值。

两步：
1、策略 更新 (policy update)

• ${\mathbf{v}}_k$ 给定， 求解 ${\pi }_{k+1}=\arg \underset{\pi }{\max }({\mathbf{r}}_{\pi }+\gamma {\mathbf{p}}_{\pi }{\mathbf{v}}_k)$

2、值 更新 (value update)

• 上一步得到的策略 ${\pi }_{k+1}$， 更新 ${\mathbf{v}}_{k+1}={\mathbf{r}}_{{\pi }_{k+1}}+\gamma {\mathbf{p}}_{{\pi }_{k+1}}{\mathbf{v}}_k$

$v_k$ 是否是一个状态值?
答案是否定的。虽然 $v_k$ 最终收敛于最优状态值，但不能保证满足任何策略的 bellman方程。例如，它一般不满足 $v_k=r_{{\pi }_k}+\gamma p_{{\pi }_k}{v}_k$ 或 $v_k=r_{{\pi }_{k+1}}+\gamma p_{{\pi }_{k+1}}{v}_k$。它只是算法生成的一个中间值。另外，由于 $v_k$ 不是状态值，所以 $q_k$ 不是动作值。

迭代流程

$v_k(s)\to q_k(s,a)\to$ 贪心策略${\pi }_{k+1}(a|s)\to$ 新的值 $v_{k+1}=\underset{a}{\max }{q}_k(s,a)$

伪代码： 值迭代算法
目标： 搜索 求解 贝尔曼最优公式的 最优状态值 和 最优策略。

遍历 每个状态 中的 每个动作， 计算 $q_k$

• 策略 更新： 选择 $q_k$ 最大的 action
• 值 更新： 将 $v_{k+1}(s)$ 更新为 计算得到的最大 $q_k$

4.1.2 例子

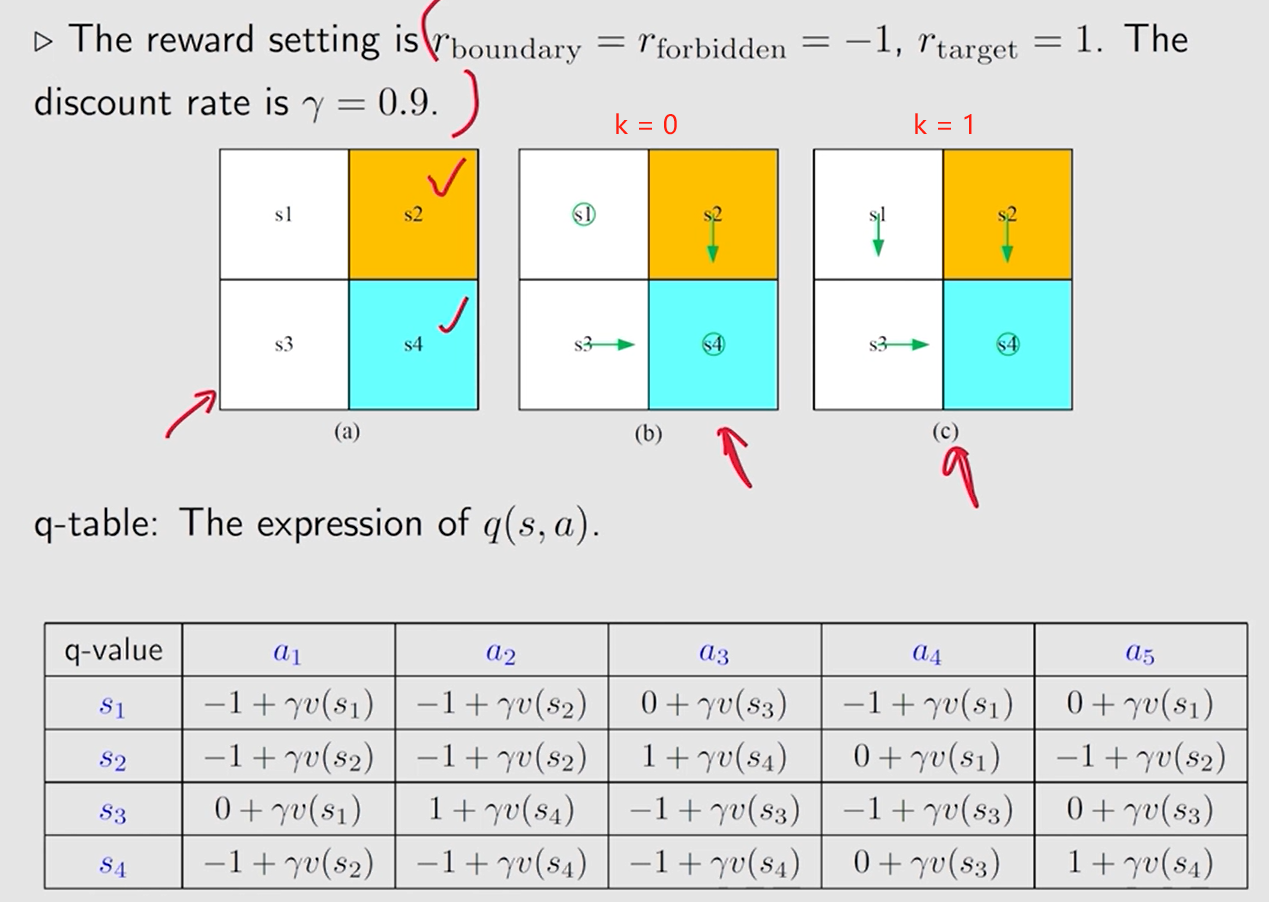
对 每个状态 的 每个动作 ，初始化 $q$ 值表

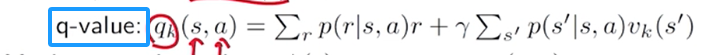
按照这里
策略更新 是将 每个状态 的 $q$ 值最大的动作 的选取概率 $\pi (a|s)$ 置为 1。     ~~~    等效于 让策略在这一步 做这个 $q$ 值最大的动作
值更新 是将 每个状态 的 值更新为 相应状态的最大 $q$ 值。

$v_0$ 可以任意选取，这里选择为 0。 不同的初值选取对迭代过程影响多大？如何根据具体情况选取合适的初值？
——> 比较直觉的是若是初始值选得离最优状态值较远， 需要的迭代次数会多些。

对于 状态 $s_1$，动作 $a_3$ 和 $a_5$ 对应的 $q$ 都是最大的， 这里直接选了 $a_5$， 有没有可能在这里选 $a_3$ 得到的才是最优策略呢？
——> 确实有可能， 所以要多次迭代，收敛后迭代结束获得的就是 最优策略。

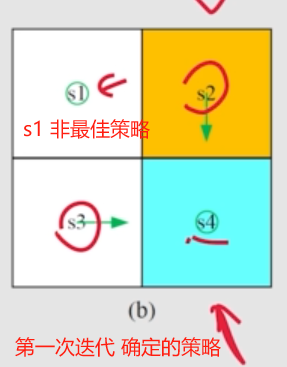
第一次 迭代， s1 没有达到 最优。

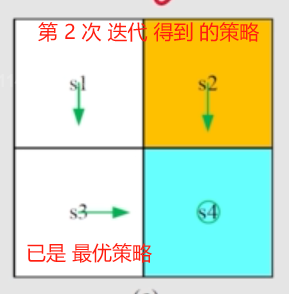
这里 迭代两次 就获得了 最优策略。

其它 更复杂情况 的迭代停止条件为：

迭代停止 则认为 获得了 最优策略。

4.2 策略迭代

主要内容： 是什么？——> 性质 ——> 如何 编程实现

任意给定的初始策略 ${\pi }_0$

两步：
1、策略 评估 (policy evaluation, pe)

• 计算 ${\pi }_k$ 的状态值： ${\mathbf{v}}_{{\pi }_k}={\mathbf{r}}_{{\pi }_k}+\gamma {\mathbf{p}}_{{\pi }_k}{\mathbf{v}}_{{\pi }_k}$求解 贝尔曼方程

策略评估做的事：通过计算相应的 状态值 来评估给定策略。

2、策略 优化 (policy improvement，pi)

• ${\pi }_{k+1}=\arg \underset{\pi }{\max }({\mathbf{r}}_{\pi }+\gamma {\mathbf{p}}_{\pi }{\mathbf{v}}_{{\pi }_k})$

迭代流程

${\pi }_0\stackrel{pe}{}{v}_{{\pi }_0}\stackrel{pi}{}{\pi }_1\stackrel{pe}{}{v}_{{\pi }_1}\stackrel{pi}{}{\pi }_2\stackrel{pe}{}{v}_{{\pi }_2}\stackrel{pi}{}...$

pe: 策略 评估
pi：策略 优化

现在处理以下几个问题：

q1：在策略评估步骤中，如何通过求解 bellman 方程得到状态值?
q2：在策略优化步骤中，为什么新策略 ${\pi }_{k+1}$ 优于 ${\pi }_k$?
q3：为什么这样的迭代算法最终可以达到最优策略?
q4：这个策略迭代算法和之前的值迭代算法是什么关系?

q1：在策略评估步骤中，如何通过求解 bellman 方程得到状态值?

如何 获取 $v_{{\pi }_k}$

已知：${\mathbf{v}}_{{\pi }_k}={\mathbf{r}}_{{\pi }_k}+\gamma {\mathbf{p}}_{{\pi }_k}{\mathbf{v}}_{{\pi }_k}$

方法一： 矩阵求逆

${\mathbf{v}}_{{\pi }_k}=(\mathbf{i}-\gamma {\mathbf{p}}_{{\pi }_k}{)}^{-1}{\mathbf{r}}_{{\pi }_k}$

方法二： 迭代 ✔

${\mathbf{v}}_{{\pi }_k}^{(j+1)}={\mathbf{r}}_{{\pi }_k}+\gamma {\mathbf{p}}_{{\pi }_k}{\mathbf{v}}_{{\pi }_k}^{(j)},j=0,1,2,...$

策略迭代 是在策略评估步骤中嵌入另一个迭代算法的迭代算法！

q2：在策略优化步骤中，为什么新策略 ${\pi }_{k+1}$ 优于 ${\pi }_k$?

• 证明 1： 在策略优化步骤中，为什么新策略 ${\pi }_{k+1}$ 优于 ${\pi }_k$?    ~~    p73-

q3：为什么策略迭代算法最终可以找到最优策略?

由于每次迭代都会改进策略， 即

${\mathbf{v}}_{{\pi }_0}\le {\mathbf{v}}_{{\pi }_1}\le {\mathbf{v}}_{{\pi }_2}\le \cdots \le {\mathbf{v}}_{{\pi }_k}\le \cdots \le {\mathbf{v}}^{\ast }$

${\mathbf{v}}_{{\pi }_k}$ 不断减小并最终收敛。仍需证明 将收敛到 ${\mathbf{v}}^{\ast }$。

定理 4.1 (策略迭代的收敛性)。策略迭代算法生成的状态值序列 { v π k } k = 0 ∞ \{v_{\pi_k}\}_{k=0}^\infty {vπk​​}k=0∞​ 收敛到最优状态值 $v^{\ast }$。因此，策略序列 { π k } k = 0 ∞ \{\pi_k\}_{k=0}^\infty {πk​}k=0∞​ 收敛到最优策略。

• 证明 2: 证明策略迭代会收敛到 最优策略 p75

证明的思路是证明 策略迭代算法 比 值迭代算法 收敛得更快。

如果 策略迭代 和 值迭代 从相同的初始猜测开始，由于 策略迭代 算法的收敛性，策略迭代 将比 值迭代 收敛得更快。

q4：这个策略迭代算法和之前的值迭代算法是什么关系?

值迭代 和 策略迭代 是 截断策略迭代 的两个极端， 后续将进一步说明。

——————————————————
如何 实现 策略迭代算法？

策略迭代 算法：
目标： 搜索 最优状态值 和 最优策略

策略迭代算法 生成的中间值是是 状态值。 因为这些值是当前策略的 bellman 方程的解。

4.2.3 例子

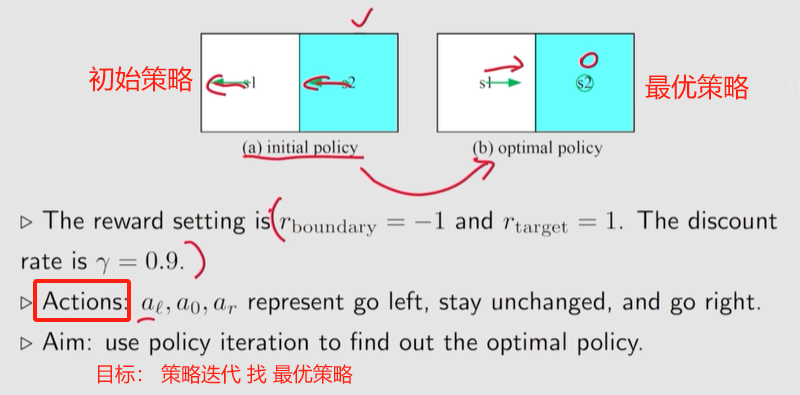
一个 示例 p79
发现一个有趣的现象：接近目标的状态 的策略 先变好， 远离目标的状态的策略会后变好。

在某一个状态， 选择 greedy action 时, 严重依赖于 其它状态的策略。
若其它状态的策略是不好的， 此时虽然选一个 动作值 ($q$) 最大的 动作， 可能意义不大；
如果 其它状态 有能够到达目标区域 的策略， 选择变到那个状态，也能到达目标区域， 得到正的 reward。

当某个状态周围 没有状态 能够到达 目标区域 的时候， 这个状态无法到达目标区域。
当周围有状态能够到达目标区域的策略时， 新的策略也能到达目标区域。

4.3 截断策略迭代

值迭代 算法和 策略迭代 算法是截断策略迭代算法的两种特殊情况。

！！每一步的等号右侧 都有的：$\mathbf{r}+\gamma \mathbf{p}\mathbf{v}$

从相同的初始条件开始。
前三个步骤是相同的。
第四步就不一样了：

• 策略迭代，求解 $v_{{\pi }_1}=r_{{\pi }_1}+\gamma p_{{\pi }_1}{v}_{{\pi }_1}$ 需要一个迭代算法 ( 迭代无数次 )
• 值迭代，$v_1=r_{{\pi }_1}+\gamma p_{{\pi }_1}{v}_0$ 是一步迭代。

每步求解 $\mathbf{v}$ 值时， 值迭代 需要一步， 策略迭代需要无穷步，迭代次数取中间值如何呢？

值迭代算法：计算一次。
策略迭代算法：计算无限次迭代。
截断策略迭代算法：计算一个有限次迭代(例如 $j$ )。从 $j$ 到 $\infty$ 的其余迭代被截断。

算法中的 $v_k$ 和 $v_k^{(j)}$ 不是状态值,是真实状态值的近似值，因为在策略评估步骤中只执行有限次迭代。

只有当我们在 策略评估 步骤中运行无限次迭代时，才能获得真实的状态值。

截断策略迭代 会不会 结束迭代时是一个 发散的结果？

• 证明。参考 电子书 pdf p83

——————————————

证明： 截断策略迭代算法 的收敛性。

因为

$v_{{\pi }_k}^{(j)}=r_{{\pi }_k}+\gamma p_{{\pi }_k}{v}_{{\pi }_k}^{(j-1)}$

$v_{{\pi }_k}^{(j+1)}=r_{{\pi }_k}+\gamma p_{{\pi }_k}{v}_{{\pi }_k}^{(j)}$

则

$v_{{\pi }_k}^{(j+1)}-v_{{\pi }_k}^{(j)}=\gamma p_{{\pi }_k}(v_{{\pi }_k}^{(j)}-v_{{\pi }_k}^{(j-1)})=\cdots ={\gamma }^j{p}_{{\pi }_k}^j(v_{{\pi }_k}^{(1)}-v_{{\pi }_k}^{(0)})$

$v_{{\pi }_k}^{(0)}=v_{{\pi }_{k-1}}$ 上一轮迭代的结果

$\begin{array}{rl}{v}_{{\pi }_k}^{(1)}& =r_{{\pi }_k}+\gamma p_{{\pi }_k}{v}_{{\pi }_k}^{(0)}\\ & =r_{{\pi }_k}+\gamma p_{{\pi }_k}{v}_{{\pi }_{k-1}}\\ & \ge r_{{\pi }_{k-1}}+\gamma p_{{\pi }_{k-1}}{v}_{{\pi }_{k-1}}①\\ & =v_{{\pi }_{k-1}}\\ & =v_{{\pi }_k}^{(0)}\end{array}$

则 $v_{{\pi }_k}^{(j+1)}\ge v_{{\pi }_k}^{(j)}$。

① ${\pi }_k=\arg \underset{\pi }{\max }(r_{\pi }+\gamma p_{\pi }{v}_{{\pi }_{k-1}})$

——————————————

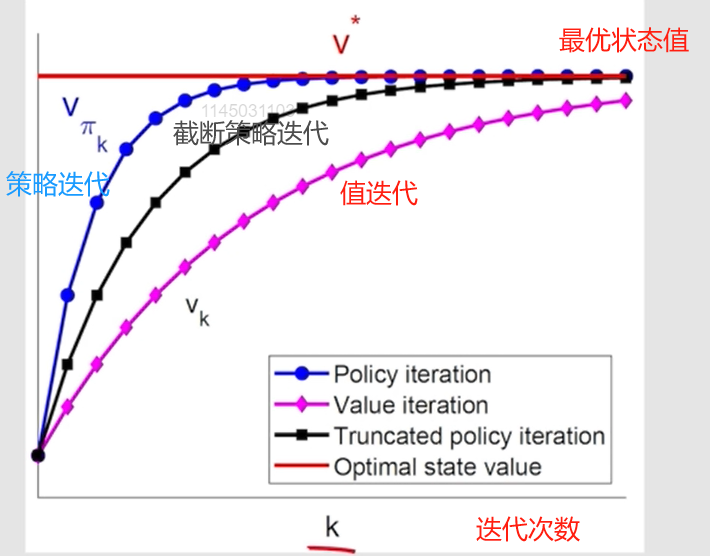
相比于策略迭代算法，截断的策略迭代算法在策略评估步骤中只需要有限次数的迭代，因此计算效率更高。与值迭代相比，截断策略迭代算法可以在策略评估步骤中多运行几次迭代，从而加快收敛速度。

pl 【策略迭代】 的收敛性证明是基于 vi 【值迭代】 的收敛性证明。由于 vi 收敛，得到 pi 收敛。

小结：

4.5
q：值迭代算法一定能找到最优策略吗?
是的。值迭代正是上一章求解 bellman 最优性方程的 压缩映射定理 所提出的算法。利用 压缩映射定理 保证了算法的收敛性。

model-based vs model-free
虽然本章介绍的算法可以找到最优策略，但由于它们需要系统模型，通常被称为动态规划算法而不是强化学习算法。
强化学习算法可以分为两类：基于模型的和免模型的。
这里，“基于模型的”并不是指系统模型的需求。相反，基于模型的强化学习使用数据来估计系统模型，并在学习过程中使用该模型。相比之下，免模型强化学习在学习过程中不涉及模型估计。

——————
习题

值迭代、策略迭代、截断策略迭代

值迭代算法中间产生的值不一定对应某些策略的状态值，这些只是产生的一些中间过程的数值，没有特别的含义。

压缩映射定理给出的算法 实际是 值迭代算法。

策略迭代算法 同时获得 最优状态值 和 最优策略。 【策略评估 需要计算状态值】

补充

证明 1： 在策略优化步骤中，为什么新策略 ${\pi }_{k+1}$ 优于 ${\pi }_k$?    ~~    p73-

证明 2： 证明策略迭代会收敛到 最优策略 p75

定理 4.1 (策略迭代的收敛性)。策略迭代算法生成的状态值序列 { v π k } k = 0 ∞ \{v_{\pi_k}\}_{k=0}^\infty {vπk​​}k=0∞​ 收敛到最优状态值 $v^{\ast }$。因此，策略序列 { π k } k = 0 ∞ \{\pi_k\}_{k=0}^\infty {πk​}k=0∞​ 收敛到最优策略。

证明的思路是证明 策略迭代算法 比 值迭代算法 收敛得更快。

——————————
证明：
为了 证明 { v π k } k = 0 ∞ \{v_{\pi_k}\}_{k=0}^\infty {vπk​​}k=0∞​ 的收敛性， 引入由以下式子生成的 另一个序列 { v k } k = 0 ∞ \{v_k\}_{k=0}^\infty {vk​}k=0∞​ 。

$v_{k+1}=f(v_k)=\underset{\pi }{\max }(r_{\pi }+\gamma p_{\pi }{v}_k)$

这个迭代算法 正是 值迭代算法，则给定任意初始值 $v_0$, $v_k$ 收敛到 $v^{\ast }$。

$k=1$， 对任意 ${\pi }_0$, 有 $v_{{\pi }_0}\ge v_0$。

通过 归纳法 证明 对任意 $k$, 有 $v_k\le v_{{\pi }_k}\le v^{\ast }$。

对 $k\ge 0$， 假设 $v_{{\pi }_k}\ge v_k$。

用到的一些中间式:

① $v_{{\pi }_{k+1}}\ge v_{{\pi }_k}$ 【上面的 证明 1 已证。即 策略优化后的策略的状态值 比之前的大】 , $p_{{\pi }_{k+1}}\ge 0$
② 令 ${\pi }_k^{\prime }=\arg \underset{\pi }{\max }(r_{\pi }+\gamma p_{\pi }{v}_k)$
③ ${\pi }_{k+1}=\arg \underset{\pi }{\max }(r_{\pi }+\gamma p_{\pi }{v}_{{\pi }_k})$

对于 $k+1$ 有：

$\begin{array}{rl}{v}_{{\pi }_{k+1}}-v_{k+1}& =(r_{{\pi }_{k+1}}+\gamma p_{{\pi }_{k+1}}{v}_{{\pi }_{k+1}})-\underset{\pi }{\max }(r_{\pi }+\gamma p_{\pi }{v}_k)\\ & \ge (r_{{\pi }_{k+1}}+\gamma p_{{\pi }_{k+1}}{v}_{{\pi }_k})-\underset{\pi }{\max }(r_{\pi }+\gamma p_{\pi }{v}_k)①\\ & =(r_{{\pi }_{k+1}}+\gamma p_{{\pi }_{k+1}}{v}_{{\pi }_k})-(r_{{\pi }_k^{\prime }}+\gamma p_{{\pi }_k^{\prime }}{v}_k)②\\ & \ge (r_{{\pi }_k^{\prime }}+\gamma p_{{\pi }_k^{\prime }}{v}_{{\pi }_k})-(r_{{\pi }_k^{\prime }}+\gamma p_{{\pi }_k^{\prime }}{v}_k)③\\ & =\gamma p_{{\pi }_k^{\prime }}(v_{{\pi }_k}-v_k)\end{array}$

因为 $v_{{\pi }_k}-v_k\ge 0$ 且 $p_{{\pi }_k^{\prime }}$ 非负。

则 $\gamma p_{{\pi }_k^{\prime }}(v_{{\pi }_k}-v_k)\ge 0$

$v_{{\pi }_{k+1}}-v_{k+1}\ge 0$

归纳得到, 对任意 $k>0$， $v_k\le v_{{\pi }_k}\le v^{\ast }$。
而 $v_k$ 收敛到 $v^{\ast }$, 由夹逼准则可得， $v_{{\pi }_k}$ 也收敛到 $v^{\ast }$