

前言
- 对撞指针从两端向中间移动。一个指针从最左端开始,另⼀个从最右端开始,然后逐渐往中间逼
近。 - 对撞指针的终止条件一般是两个指针相遇或者错开(也可能在循环内部找到结果直接跳出循
环),也就是: -
- left == right (两个指针指向同一个位置)
-
- left > right (两个指针错开)
快慢指针的实现方式有很多种,最常用的⼀种就是:
- 在一次循环中,每次让慢的指针向后移动一位,而快的指针往后移动两位,实现一快一慢。
1. 移动零(easy)
「数组分两块」是非常常见的一种题型,主要就是根据一种划分方式,将数组的内容分成左右两部
分。这种类型的题,⼀般就是使用「双指针」来解决。
题目链接: 283. 移动零
题目描述:
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
示例 1:
示例 2:
提示:
2. 解法(快排的思想:数组划分区间 - 数组分两块)
算法思路:
算法流程:
- 初始化 cur = 0 (用来遍历数组), dest = -1 (指向非零元素序列的最后⼀个位置。
因为刚开始我们不知道最后⼀个非零元素在什么位置,因此初始化为 -1 ) - cur 依次往后遍历每个元素,遍历到的元素会有下面两种情况:
- 因为 dest 指向的位置是非零元素区间的最后⼀个位置,如果扫描到⼀个新的非零元素,那么它的位置应该在 dest + 1 的位置上,因此 dest 先自增 1 ;
- dest++ 之后,指向的元素就是 0 元素(因为非零元素区间末尾的后⼀个元素就是0 ),因此可以交换到 cur 所处的位置上,实现 [0, dest] 的元素全部都是非零元素, [dest + 1, cur - 1] 的元素全是零。

c++ 算法代码:
class solution {
public:
void movezeroes(vector<int>& nums) {
for(int des=-1,cur =0;cur<nums.size();cur++)
if(nums[cur])
swap(nums[++des],nums[cur]);
}
};
c++ 代码结果:

java 算法代码:
class solution
{
public void movezeroes(int[] nums)
{
for (int cur = 0, dest = -1; cur < nums.length; cur++)
if (nums[cur] != 0) // 仅需处理⾮零元素
{
dest++; // dest 先向后移动⼀位
// 交换
int tmp = nums[cur];
nums[cur] = nums[dest];
nums[dest] = tmp;
}
}
}
3. 复写零(easy)
题目链接: 1089. 复写零
题目描述:
示例 1:
示例 2:
提示:
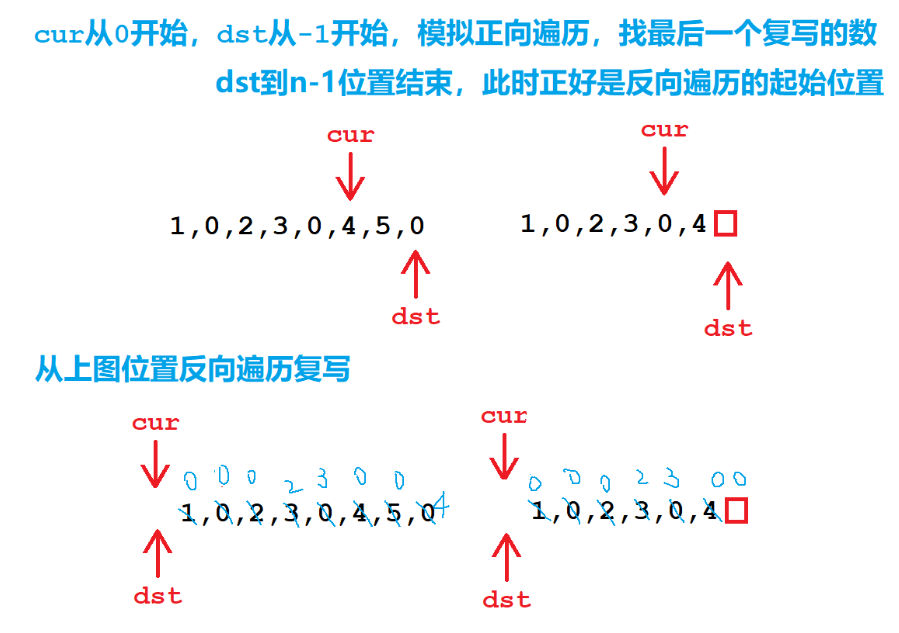
4.解法(原地复写 - 双指针)
确定目标位置:
- 首先,使用两个指针 dest 和 cur 来确定每个位置复制0后应该放置的位置。cur 指针用于遍历原始数组,而 dest 指针则用于确定在复制0后应该放置新元素的位置。cur 最终的位置就是复写后数组的最后一个数的位置。
- 从后向前复写:在确定了所有元素的目标位置后,从数组的末尾开始,根据原始数组中的元素值,将元素复制到它们的目标位置。
解题方法
时间复杂度: o(n),其中n是数组的长度。算法只进行了一次遍历,因此时间复杂度是线性的。
空间复杂度: o(1),算法只使用了常数个额外变量,没有使用与数组大小相关的额外空间。
总结
c++ 算法代码:
class solution {
public:
void duplicatezeros(vector<int>& arr) {
//找最后一个数
int dest=-1,cur=0,n=arr.size();
while(cur<n)
{
if(arr[cur])
dest++;
else
dest+=2;
if(dest>=n-1)
break;
cur++;
}
//边界情况
if(dest>=n)
{
arr[n-1]=0;
dest-=2;
cur--;
}
while(cur>=0)
{
if(arr[cur])
arr[dest--]=arr[cur--];
else
{
arr[dest--]=arr[cur];
arr[dest--]=arr[cur--];
}
}
}
};
java 算法代码:
class solution
{
public void duplicatezeros(int[] arr)
{
int cur = 0, dest = -1, n = arr.length;
// 1. 先找到最后⼀个需要复写的数
while (cur < n)
{
if (arr[cur] == 0) dest += 2;
else dest += 1;
if (dest >= n - 1) break;
cur++;
}
// 2. 处理⼀下边界情况
if (dest == n)
{
arr[n - 1] = 0;
cur--; dest -= 2;
}
// 3. 从后向前完成复写操作
while (cur >= 0)
{
if (arr[cur] != 0) arr[dest--] = arr[cur--];
else
{
arr[dest--] = 0;
arr[dest--] = 0;
cur--;
}
}
}
}





发表评论