目录
62.路径问题

解法(动态规划):
算法思路:
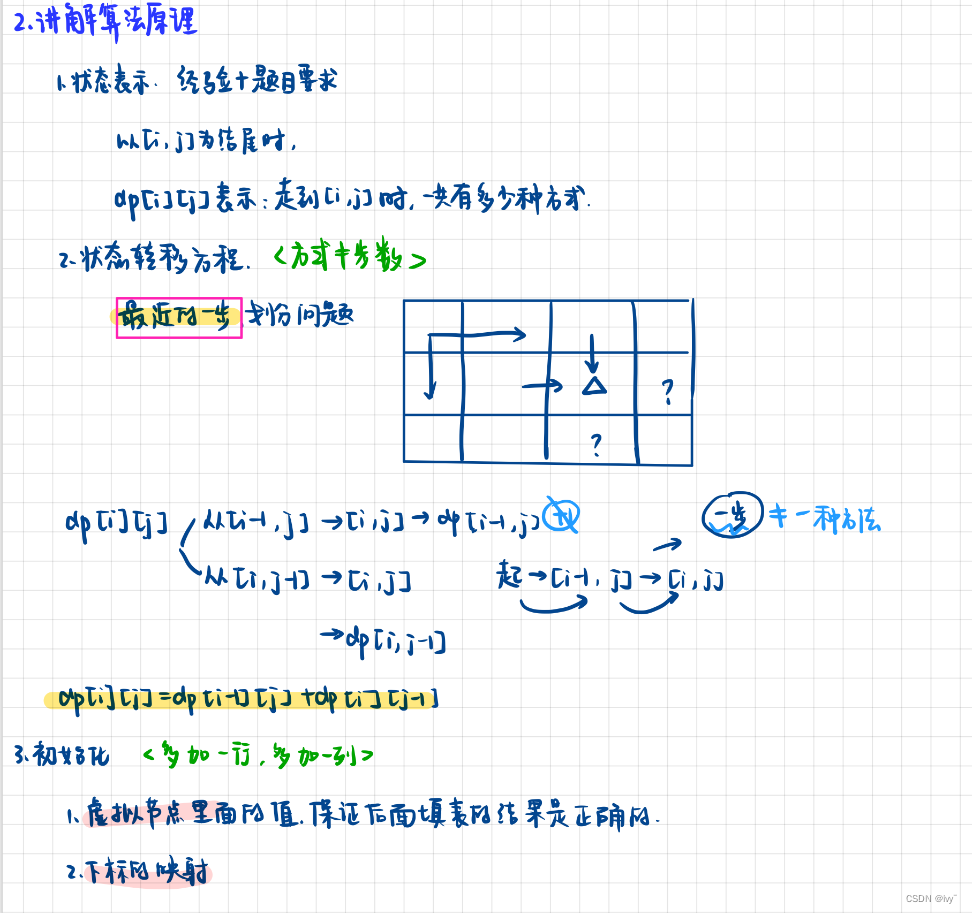
1. 状态表⽰:
对于这种「路径类」的问题,我们的状态表⽰⼀般有两种形式:
2. 状态转移⽅程:
简单分析⼀下。如果dp[i][j] 表⽰到达[i, j] 位置的⽅法数,那么到达[i, j] 位置之 前的⼀⼩步,有两种情况:
3. 初始化:
可以在最前⾯加上⼀个「辅助结点」,帮助我们初始化。使⽤这种技巧要注意两个点:
在本题中,「添加⼀⾏」,并且「添加⼀列」后,只需将dp[0][1] 的位置初始化为1 即可。
4. 填表顺序:
根据「状态转移⽅程」的推导来看,
填表的顺序就是「从上往下」填每⼀⾏,在填写每⼀⾏的时候 「从左往右」。
5. 返回值:
根据「状态表⽰」,我们要返回dp[m][n] 的值。
代码:
class solution
{
public:
int uniquepaths(int m, int n)
{
vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0)); // 创建⼀个 dp表
dp[0][1] = 1; // 初始化
// 填表
for (int i = 1; i <= m; i++) // 从上往下
for (int j = 1; j <= n; j++) // 从左往右
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
// 返回结果
return dp[m][n];
}
};
测试:
不同路径2.0

解法(动态规划):
算法思路:
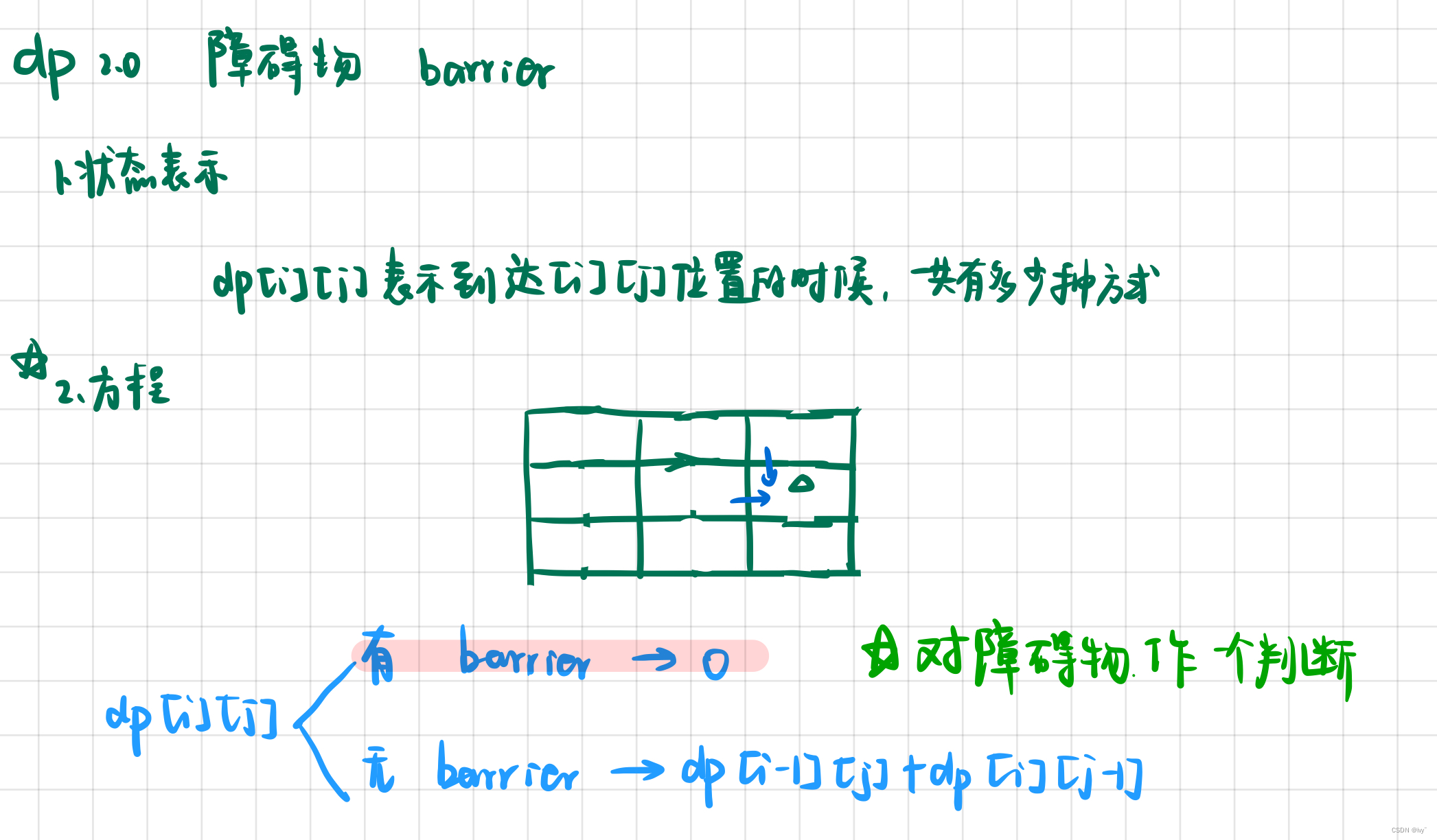
本题为不同路径的变型,只不过有些地⽅有「障碍物」,只要在「状态转移」上稍加修改就可解决。
1. 状态表⽰:
对于这种「路径类」的问题,我们的状态表⽰⼀般有两种形式:
2. 状态转移:
简单分析⼀下。如果dp[i][j] 表⽰到达[i, j] 位置的⽅法数,那么到达[i, j] 位置之 前的⼀⼩步,有两种情况:
由此我们可以得出⼀个结论,只要这个位置上「有障碍物」,那么我们就不需要计算这个位置上的 值,直接让它等于0 即可。
3. 初始化:
可以在最前⾯加上⼀个「辅助结点」,帮助我们初始化。使⽤这种技巧要注意两个点:
在本题中,「添加⼀⾏」,并且「添加⼀列」后,只需将dp[0][1] 的位置初始化为1 即可。
4. 填表顺序:
根据「状态转移⽅程」的推导来看,
填表的顺序就是「从上往下」填每⼀⾏,在填写每⼀⾏的时候 「从左往右」。
5. 返回值:
根据「状态表⽰」,我们要返回dp[m][n] 的值。
代码
class solution {
public:
int uniquepathswithobstacles(vector<vector<int>>& ob) {
// 1. 创建 dp 表
// 2. 初始化
// 3. 填表
// 4. 返回值
int m = ob.size(), n = ob[0].size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
dp[1][0] = 1;
for (int i = 1; i <= m; i++)
for (int j = 1; j <= n; j++)
if (ob[i - 1][j - 1] == 0)
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
return dp[m][n];
}
};
测试:
剑指offer47.礼物的最⼤价值

方程;
对于dp[i][j] ,我们发现想要到达[i, j] 位置,有两种⽅式:
代码:
class solution {
public:
int jewelleryvalue(vector<vector<int>>& frame) {
// 1. 创建 dp 表
// 2. 初始化
// 3. 填表
// 4. 返回结果
int m = frame.size(), n = frame[0].size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
for (int i = 1; i <= m; i++)
for (int j = 1; j <= n; j++)
dp[i][j] =
max(dp[i - 1][j], dp[i][j - 1]) + frame[i - 1][j - 1];
return dp[m][n];
}
};测试:
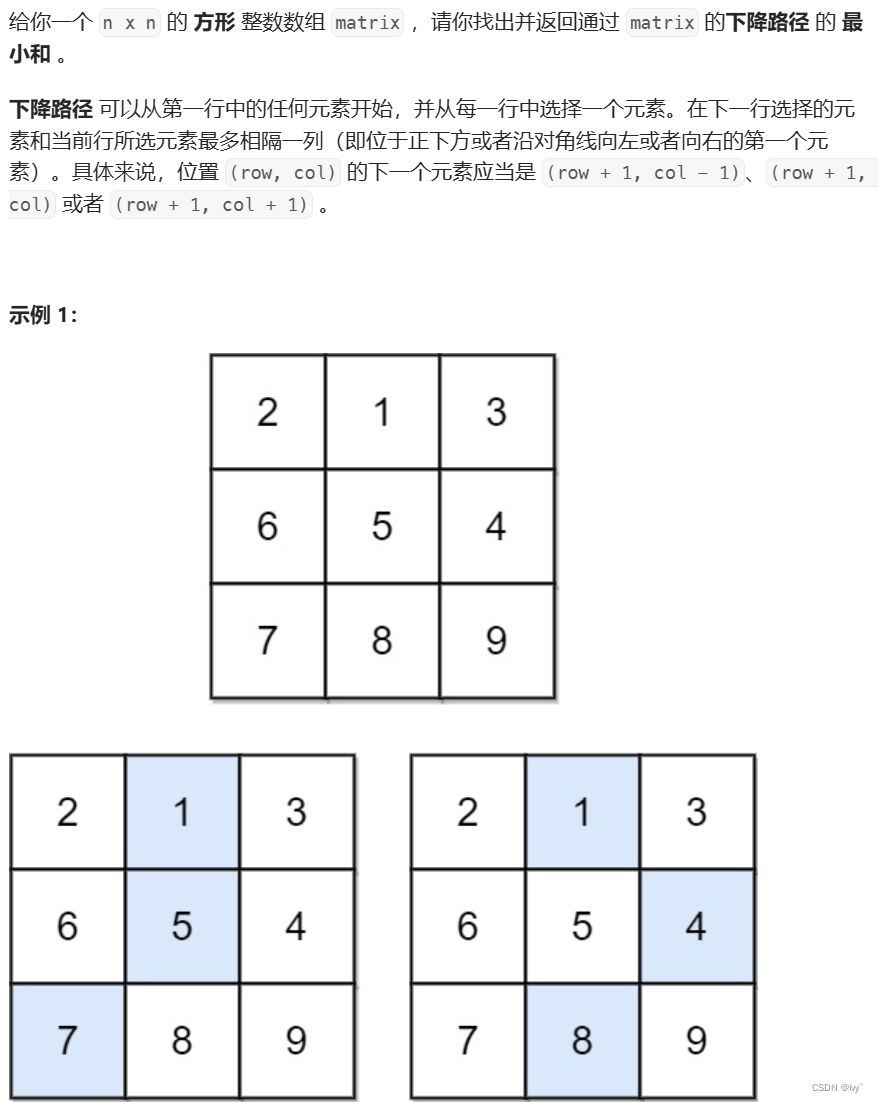
931.下降路径最小和

代码:
class solution {
public:
int minfallingpathsum(vector<vector<int>>& matrix) {
// 1. 创建 dp 表
// 2. 初始化
// 3. 填表
// 4. 返回结果
int n = matrix.size();
vector<vector<int>> dp(n + 1, vector<int>(n + 2, int_max));
// 初始化第⼀⾏
for (int j = 0; j < n + 2; j++)
dp[0][j] = 0;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
dp[i][j] =
min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i - 1][j + 1])) +
matrix[i - 1][j - 1];//每次只能min两个
int ret = int_max;
for (int j = 1; j <= n; j++)
ret = min(ret, dp[n][j]);
return ret;
}
};
64.最小路径和

代码:
class solution {
public:
int minpathsum(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1, int_max));
dp[0][1] = dp[1][0] = 0;
for (int i = 1; i <= m; i++)
for (int j = 1; j <= n; j++)
dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i - 1][j - 1];
return dp[m][n];
}
};【困难题】 174.地下城游戏(视频讲解)
恶魔们抓住了公主并将她关在了地下城 dungeon 的 右下角 。地下城是由 m x n 个房间组成的二维网格。我们英勇的骑士最初被安置在 左上角 的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。
骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下,他会立即死亡。
有些房间由恶魔守卫,因此骑士在进入这些房间时会失去健康点数(若房间里的值为负整数,则表示骑士将损失健康点数);其他房间要么是空的(房间里的值为 0),要么包含增加骑士健康点数的魔法球(若房间里的值为正整数,则表示骑士将增加健康点数)。
为了尽快解救公主,骑士决定每次只 向右 或 向下 移动一步。
返回确保骑士能够拯救到公主所需的最低初始健康点数。
注意:任何房间都可能对骑士的健康点数造成威胁,也可能增加骑士的健康点数,包括骑士进入的左上角房间以及公主被监禁的右下角房间。

代码:
class solution {
public:
int calculateminimumhp(vector<vector<int>>& dungeon) {
if (dungeon.empty() || dungeon[0].empty()) {
return 0;
}
int m = dungeon.size(), n = dungeon[0].size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1, int_max));
dp[m][n-1] = dp[m-1][n] = 1; //假设为1,因为后面要取正数的
for (int i = m - 1; i >= 0; --i) {
for (int j = n - 1; j >= 0; --j) {
int minhealth = min(dp[i+1][j], dp[i][j+1]) - dungeon[i][j];
dp[i][j] = max(1, minhealth);
}
}
return dp[0][0];
}
};
困难题还是有困难的原因的qwq
leetcode 地下城游戏 的一个问题理解
还有一点就是 dp[m][n-1] = dp[m-1][n] = 1
可以理解为他救完公主之后还要有一点血,才能活着
总结:





发表评论