【c语言】链表带环问题分析及顺序表链表对比分析

🔥个人主页:大白的编程日记
🔥专栏:c语言学习之路

文章目录
前言
一.顺序表和链表对比
1.1顺序表和链表的区别
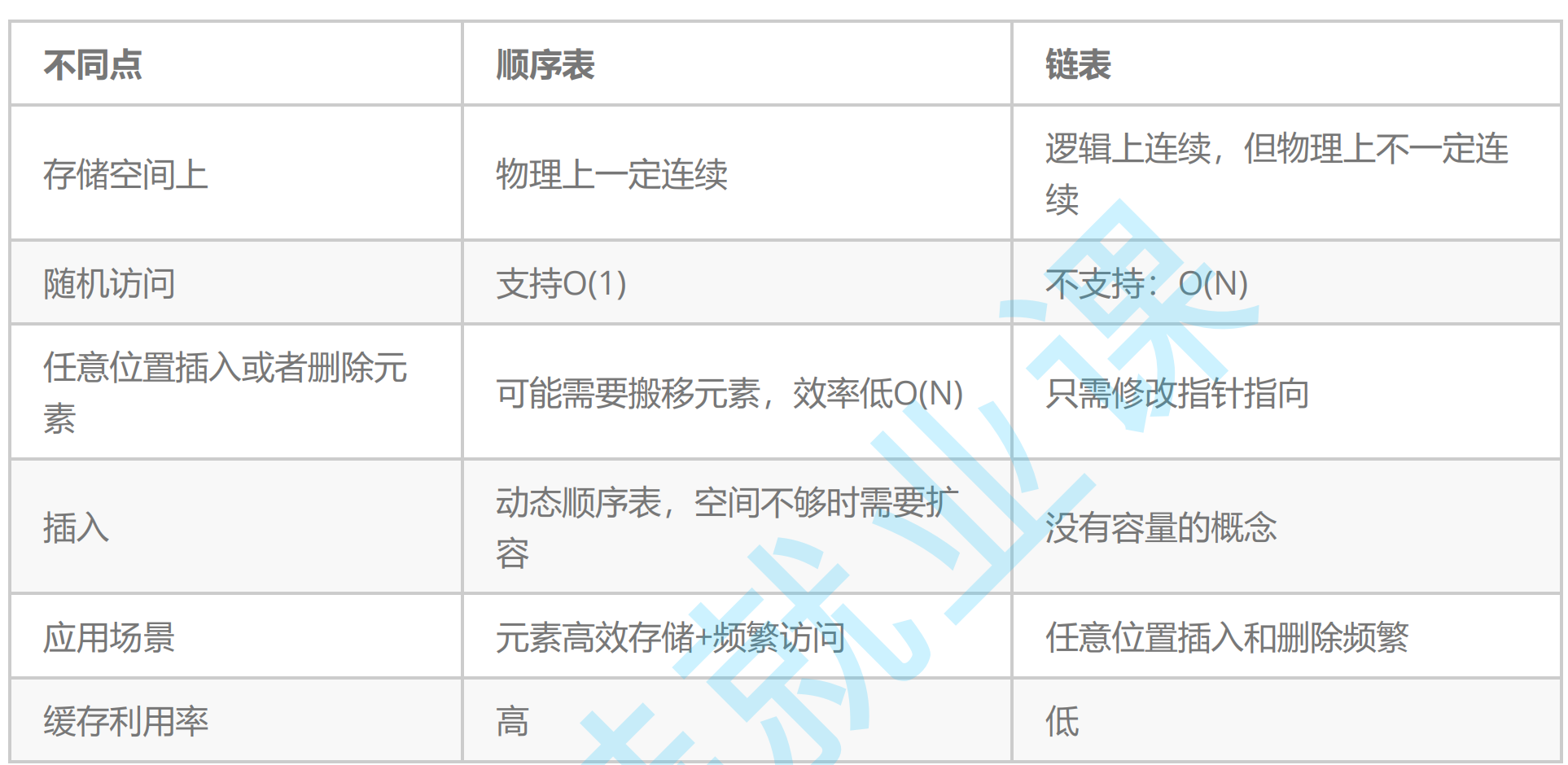
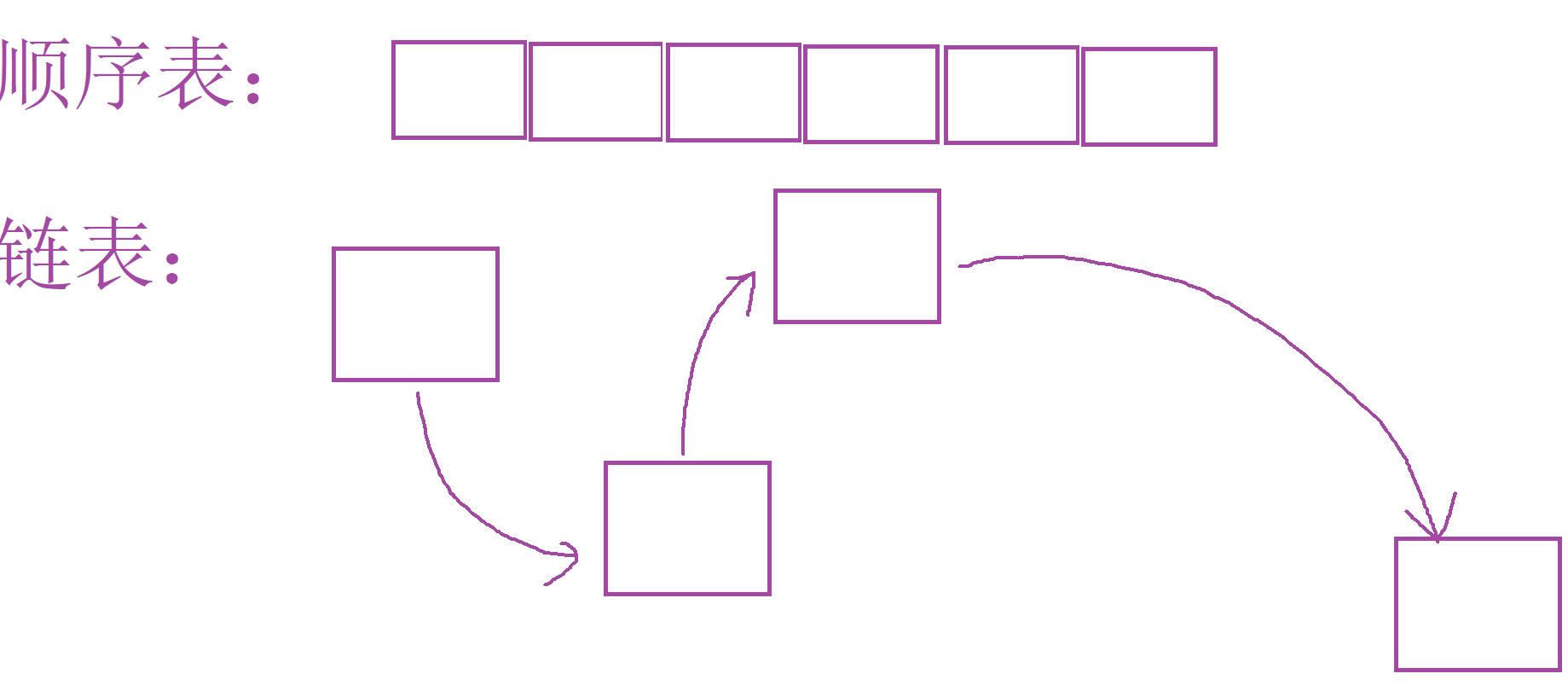
- 存储空间
顺序表:物理上是连续的。
链表:因为链表是由节点组成,每个节点由指针连接。 所以在逻辑上是连续的,但每个节点都是malloc动态开辟的,在物理空间上不一定连续。
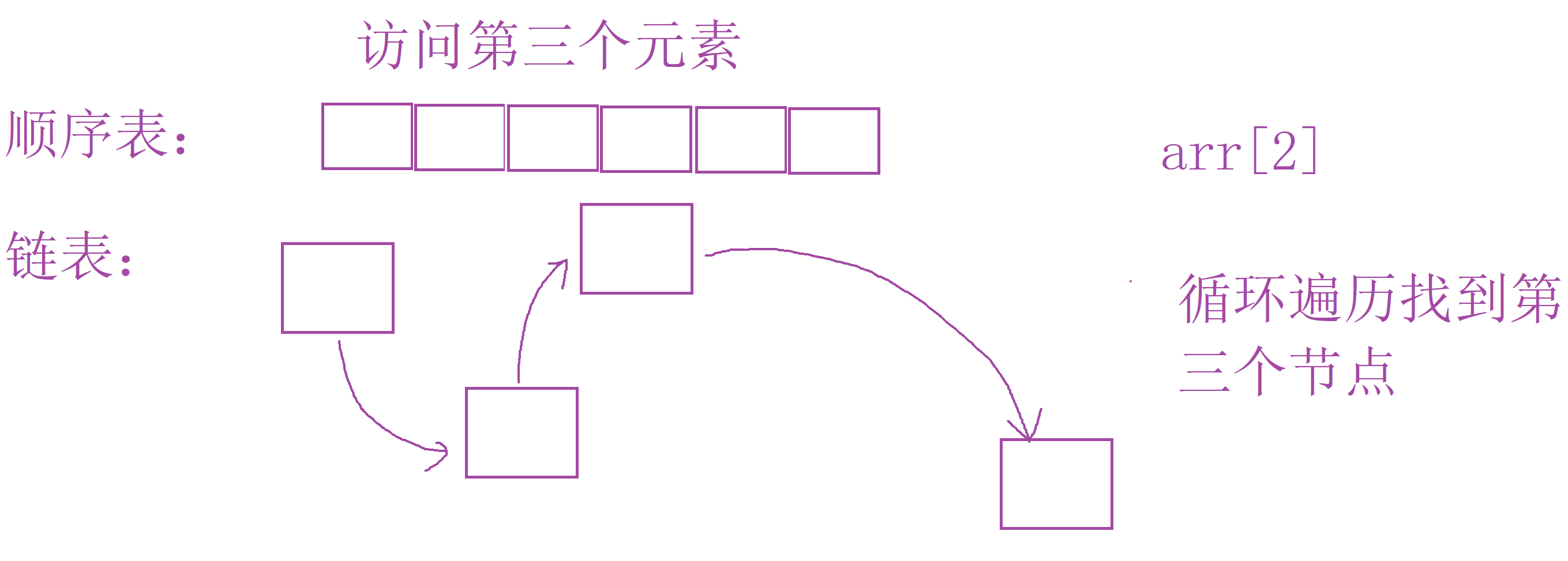
- 随机访问
顺序表:顺序表可以通过下标来进行随机访问。
链表:链表不支持随机访问,只能从头节点开始遍历寻找节点。
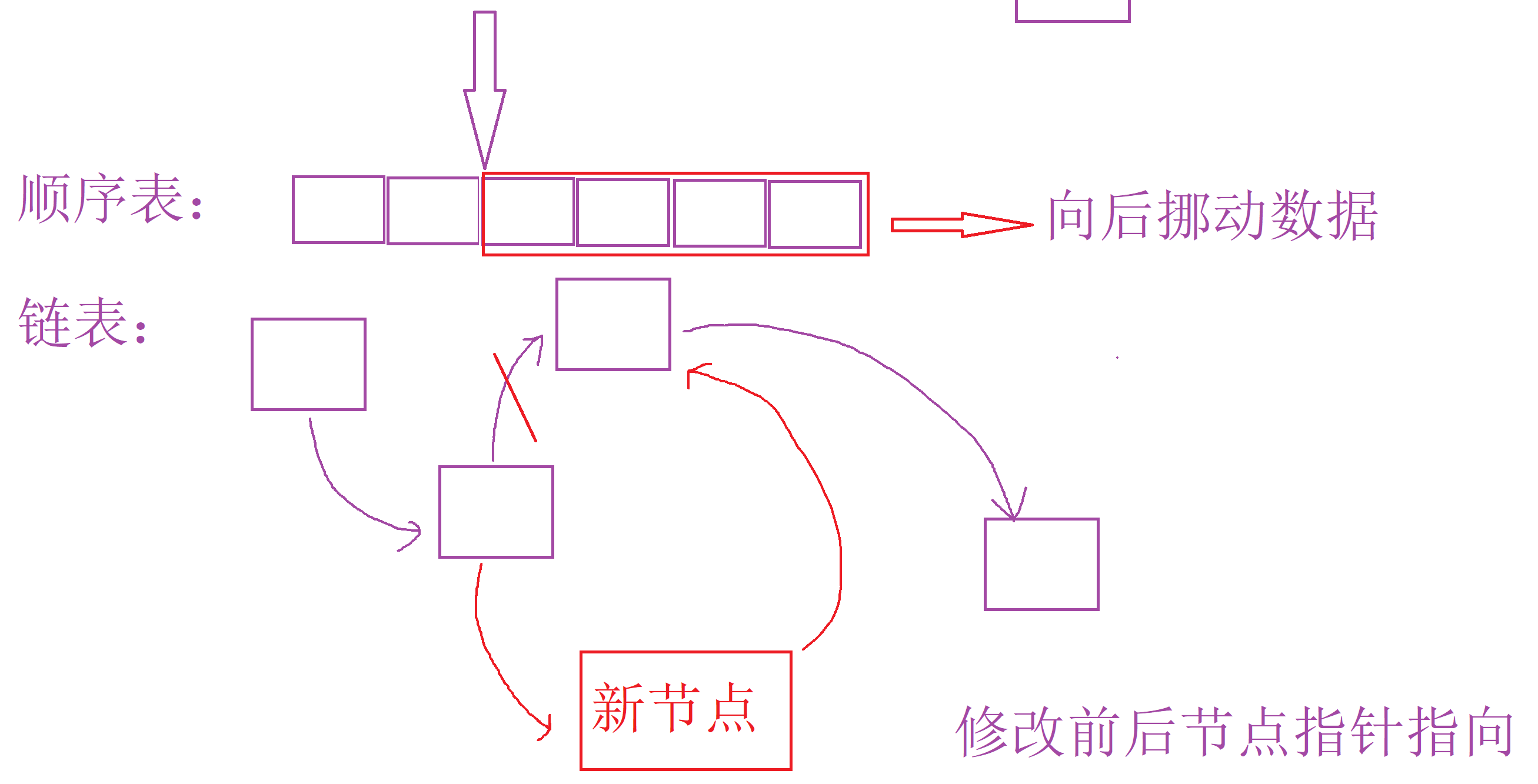
- 任意位置插入删除
顺序表:如果不是尾插尾删,需要挪动数据。
链表:链表由节点组成,插入或删除只需要修改前后节点的指针指向即可。
- 扩容
顺序表:空间不够需要扩容。
扩容realloc本身会有消耗且异地扩容消耗不小,2倍扩容可能存在空间浪费。
链表:按需申请释放,需要一个申请一个,不存在扩容,不会浪费空间。
#define _crt_secure_no_warnings 1
#include<stdio.h>
#include<stdlib.h>
int main()
{
int* p = (int*)malloc(4);
printf("%p\n", p);
int* p1 = (int*)realloc(p, 40);
printf("%p", p1);
}
异地扩容: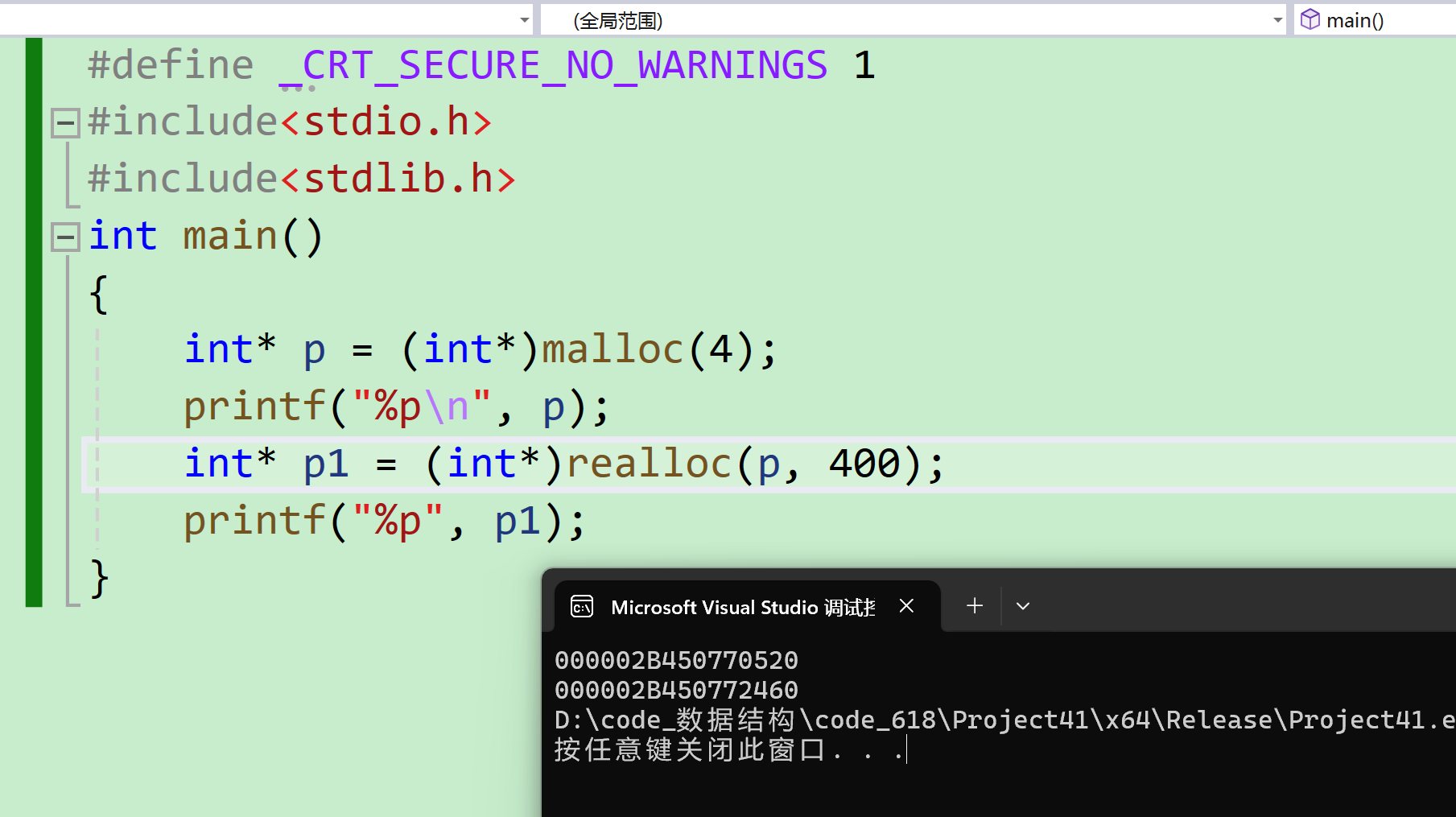
只要空间大一点,基本都是异地扩容。
原地扩容:
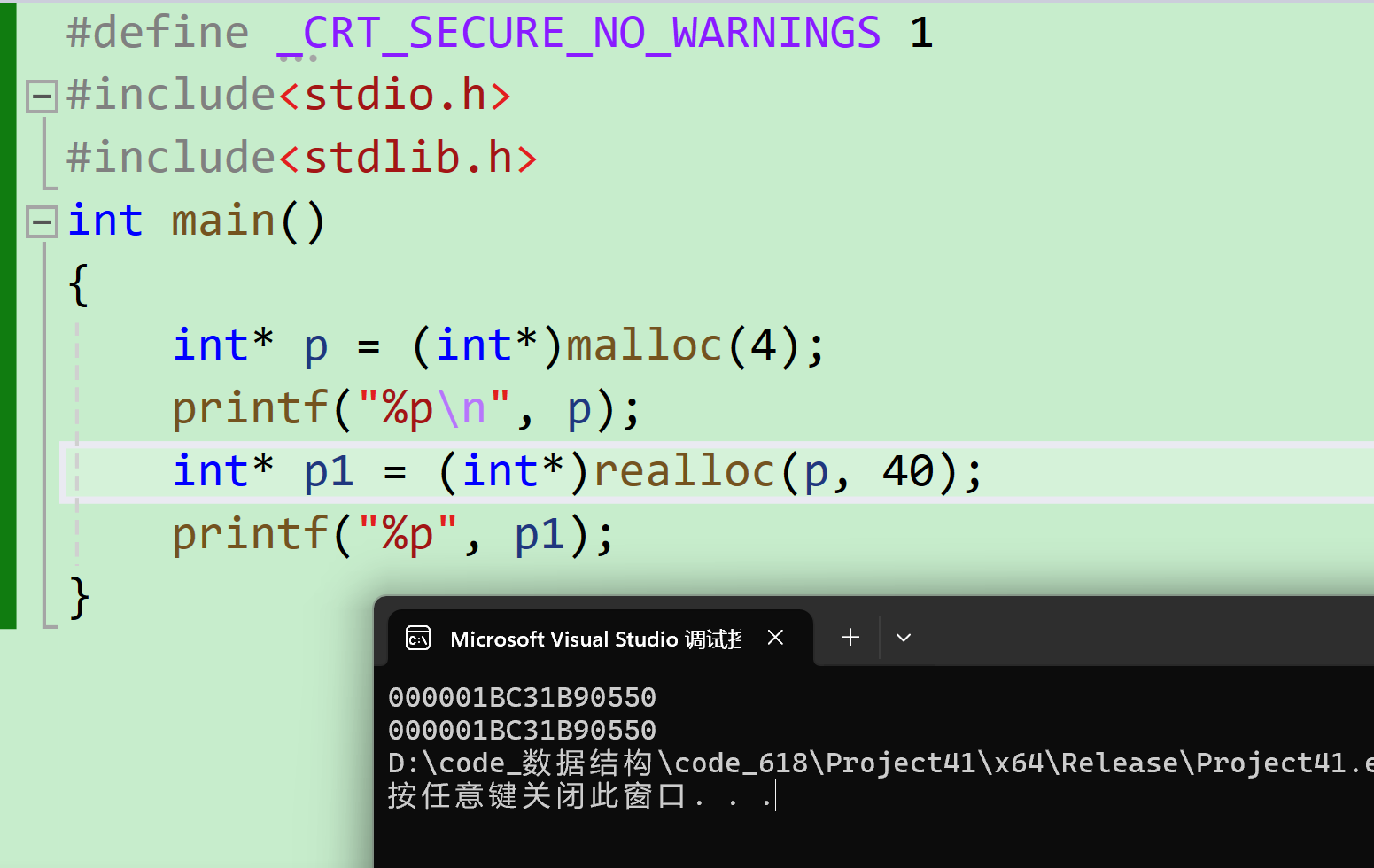
- 应用场景
1.2缓存利用率(缓存命中率)
为什么呢?什么是缓存命中率呢?
- 内存和硬盘
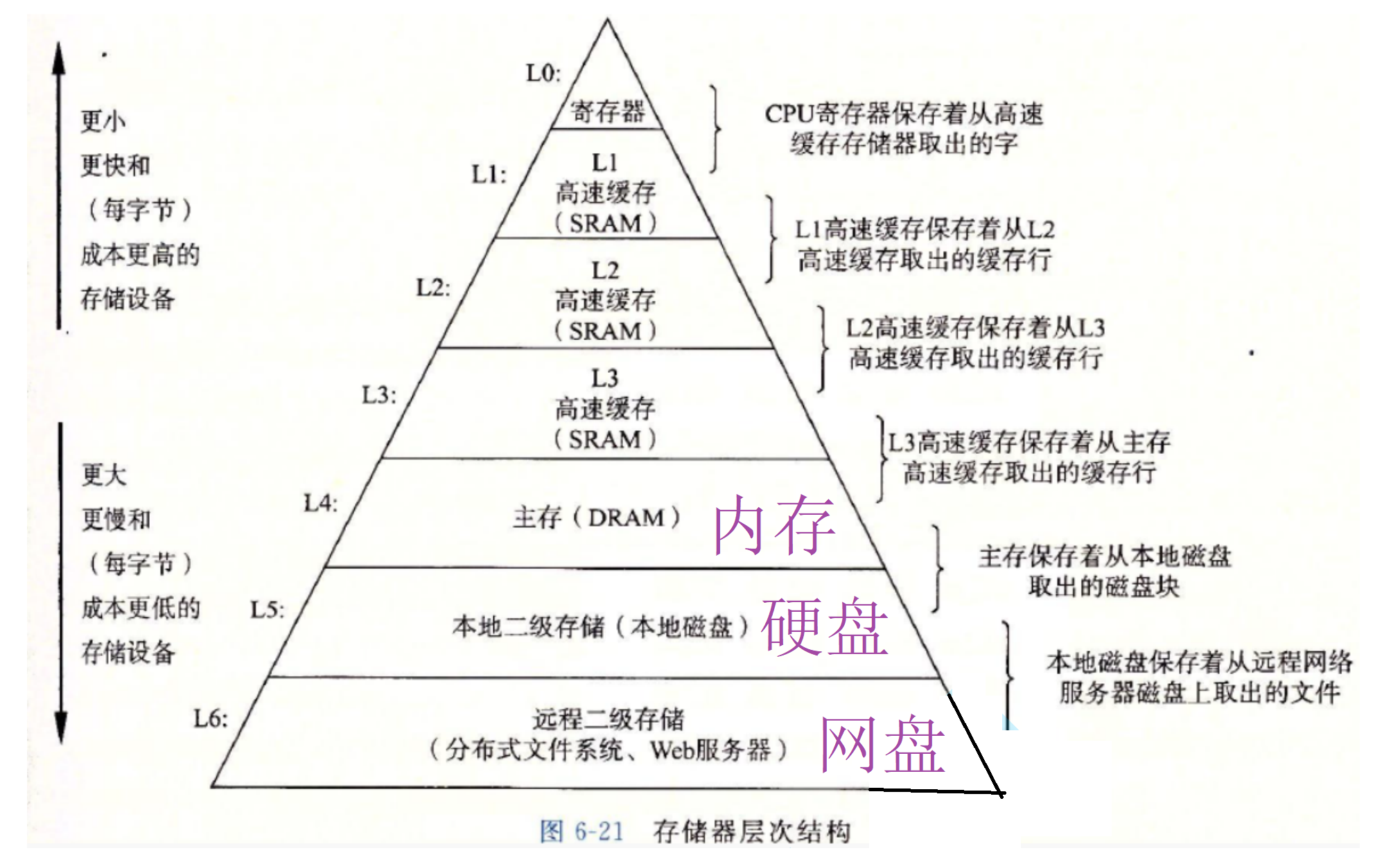
这是我们计算机的内部的存储结构。
主存也就是我们的内存和硬盘的区别就是
例如:
- 寄存器和三级缓存
那既然已经有内存,内存的速度也还行,为什么还有寄存器和三级缓存呢?
#define _crt_secure_no_warnings 1
#include<stdio.h>
#include<stdlib.h>
int main()
{
int i = 0;
int ret = i++;
}
以这段代码为例:
那为什么要这样做呢?
因为cpu和内存不同频,cpu跑的太快了。
如果直接访问内存数据进行++,因为内存太慢了。
他宁愿把内存中数据加载到寄存器中,cpu在寄存器执行指令,再把运行结果返回内存。
一般来说,cpu不会直接访问内存
-
寄存器
如果数据比较小(4或8字节)就会把数据加载到寄存器。 -
缓存
如果数据比较大就加载到缓存中。
- 缓存的加载
如果你要加载4个字节到缓存,通常会加载一长段空间到缓存中。而不只是4个字节。为什么呢?
把内存看作学校,缓存看作大巴,cpu看作度假村。
现在学校安排大巴把学生(数据)送到度假村去。

所以顺序表的缓存命中率高,
链表的缓存命中率低,而且会造成缓存污染。
如果大家想多了解缓存的话可以看这篇文章
与程序员相关的cpu缓存知识
二.链表的带环问题
2.1快慢指针
- 题目
环形链表
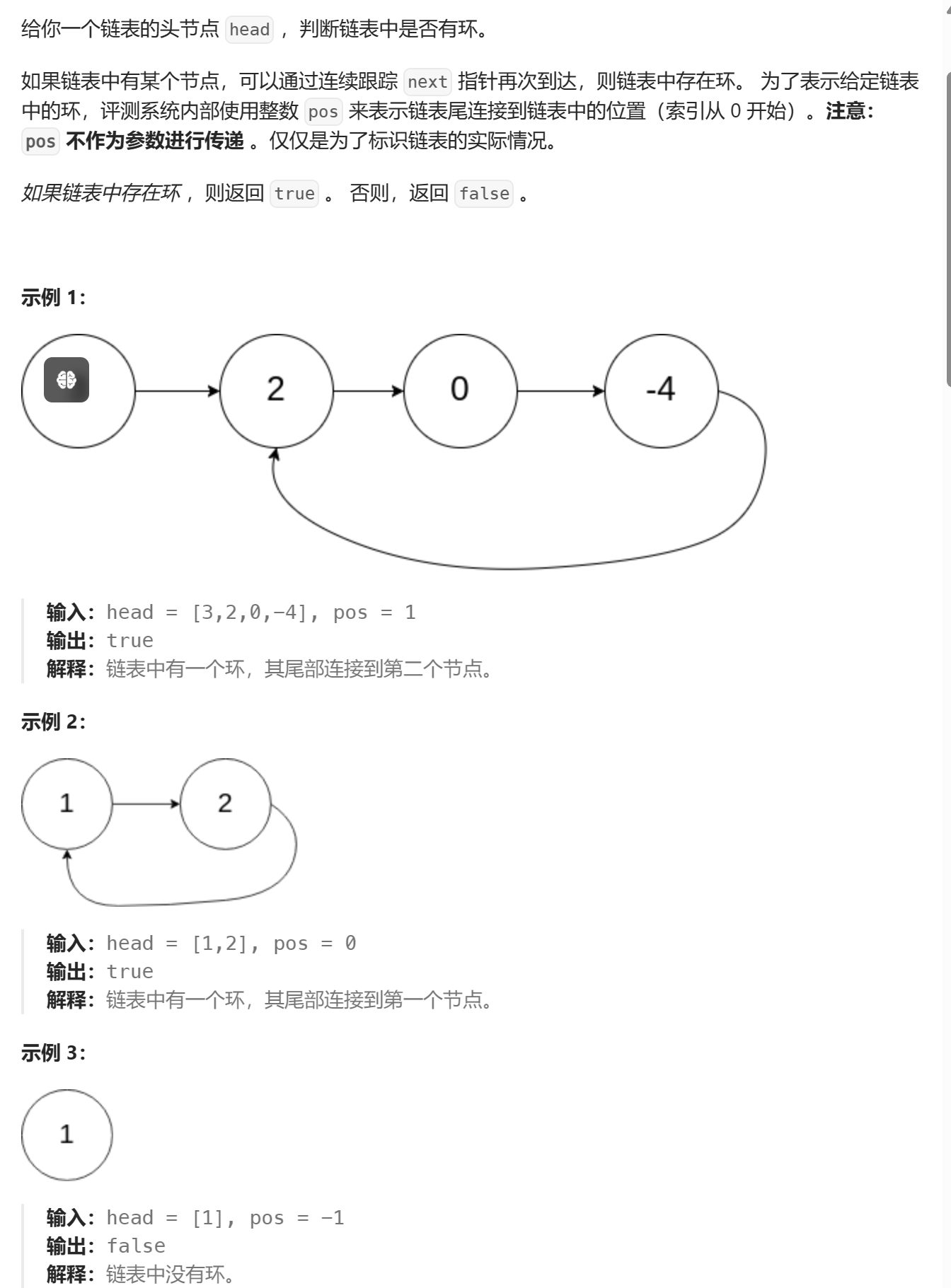
- 思路
创建一个快指针和一个慢指针,快指针一次走两步,慢指针一次走一步。
如果是链表带环,快慢指针最终会相遇。不带环,则快指针走到尾。 - 代码实现
typedef struct listnode listnode;
bool hascycle(struct listnode *head)
{
listnode*slow,*fast;
slow=fast=head;
while(fast&&fast->next)
{
slow=slow->next;//慢指针走一步
fast=fast->next->next;//快指针走两步
if(fast==slow)//快慢指针相遇
{
return true;
}
}
return false;//不带环
}
2.2证明快慢指针相遇问题
那如何证明题目一定会相遇呢?

当慢指针入环时,快指针与慢指针相差n个节点。
由于快指针每次走两步,慢指针走一步。
每次移动快指针都会与慢指针的距离缩小一个节点。
当他们的距离节点缩小为0时,就会相遇。
所以快慢指针一定能够相遇。
2.3快指针的步长
那快指针是不是只能走一步呢?如果快指针走3,4,5…n步还一定能相遇吗?
- 步长为3时
证明结果如下

我们用快慢指针步长的关系列出等式,反推证明n为奇数和c为偶数的情况不会出现,从而得出结论步长为3时一定能相遇。
-
验证
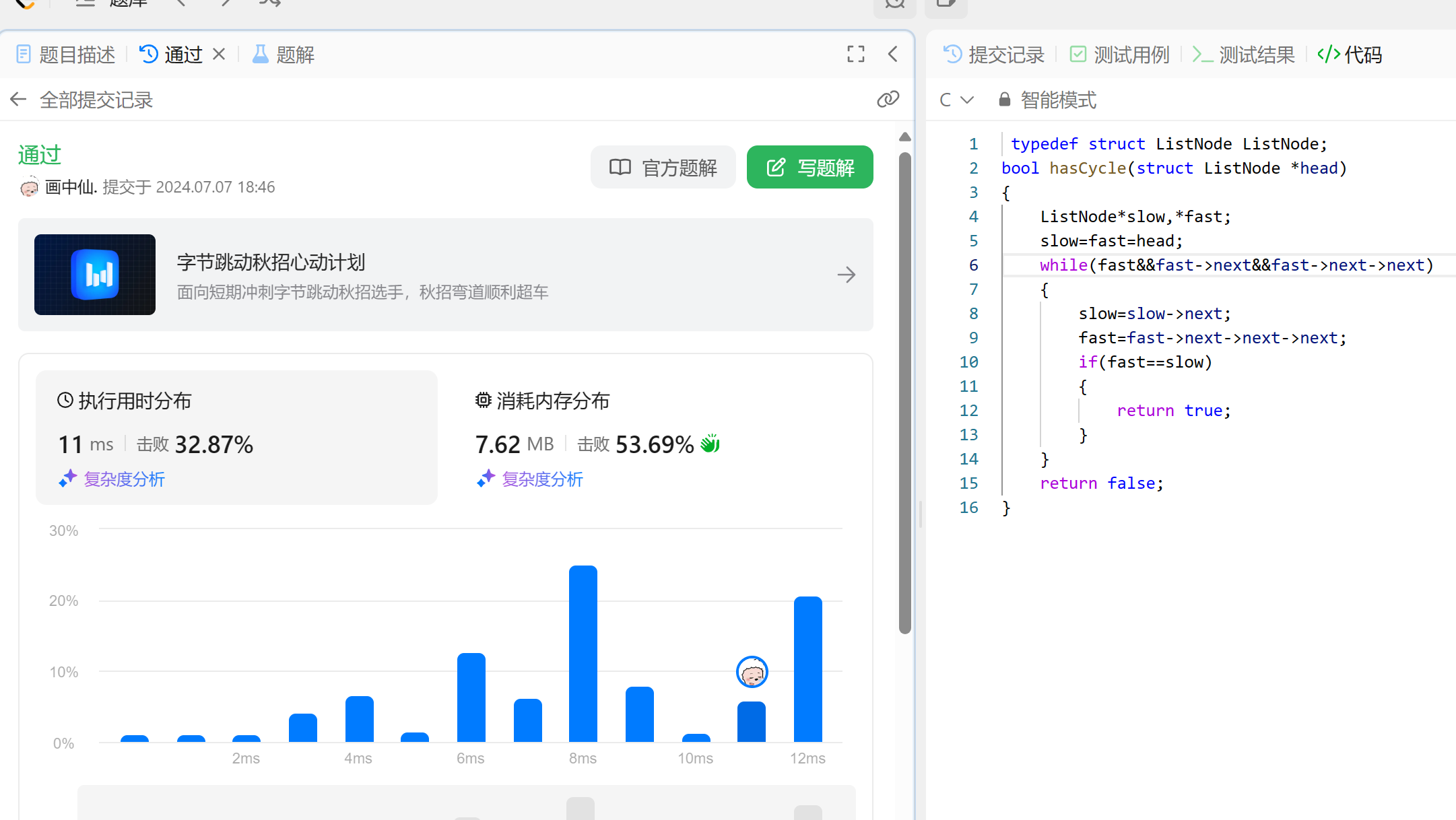
-
步长为3,4,5…n
这些情况和前面的推导证明过程相似,大家有兴趣可以自己深入探究。
2.4环的入口
-
题目
环形链表二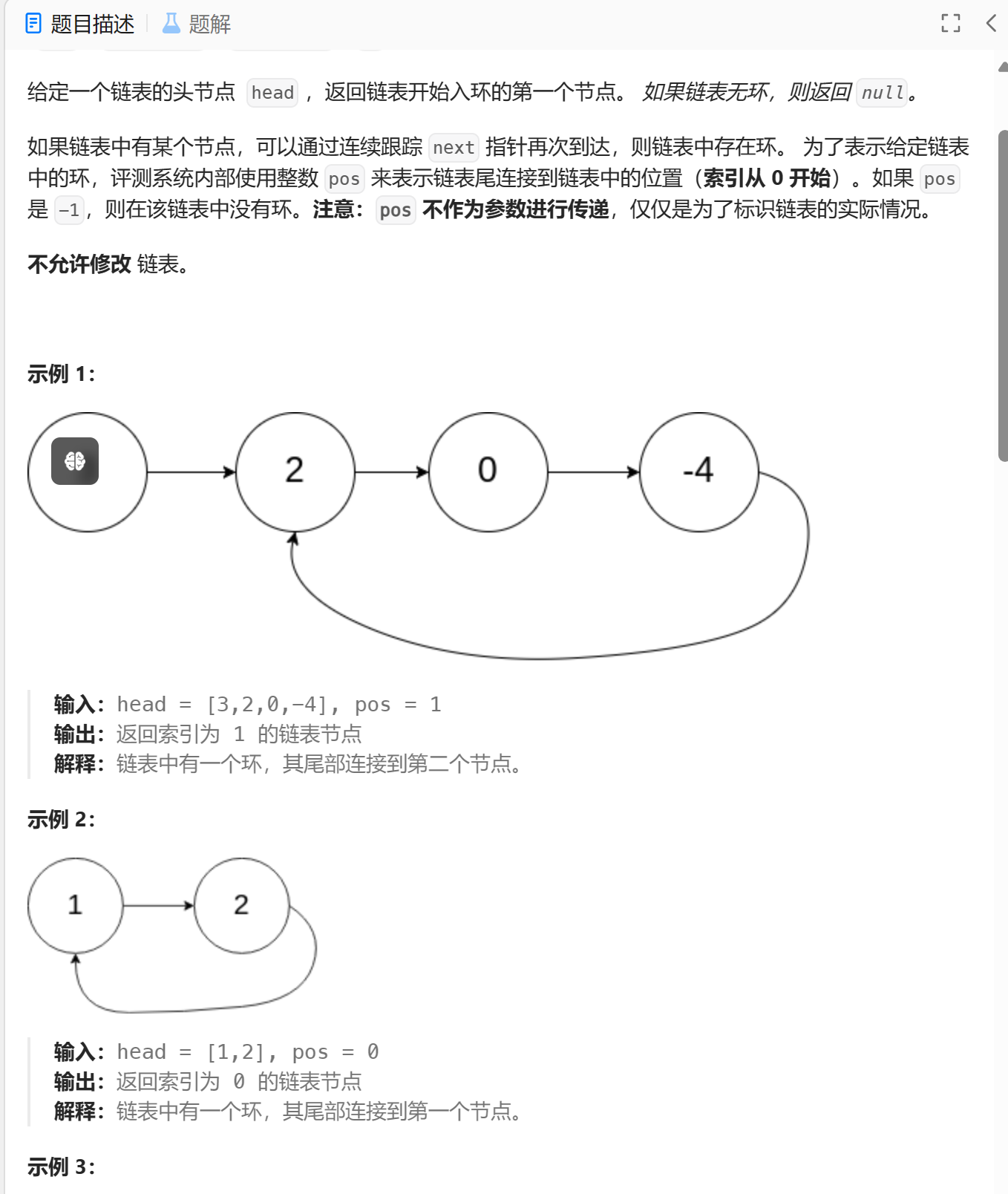
-
思路
创建一个快指针和一个慢指针,快指针一次走两步,慢指针一次走一步。
如果是链表带环,快慢指针最终会相遇。
一个指针相遇点开始走,一个指针从头节点开始走,每次两个指针都走一步。
当两个指针相遇时,相遇节点就是入环节点。
不带环,则快指针走到尾。 -
代码实现
typedef struct listnode listnode ;
struct listnode *detectcycle(struct listnode *head)
{
listnode*slow,*fast;
slow=fast=head;
while(fast&&fast->next)
{
fast=fast->next->next;
slow=slow->next;
if(slow==fast)
{
listnode* pcur=slow;
while(pcur!=head)
{
pcur=pcur->next;
head=head->next;
}
return pcur;
}
}
return null;
}
- 证明
具体证明过程如下:

- 验证
-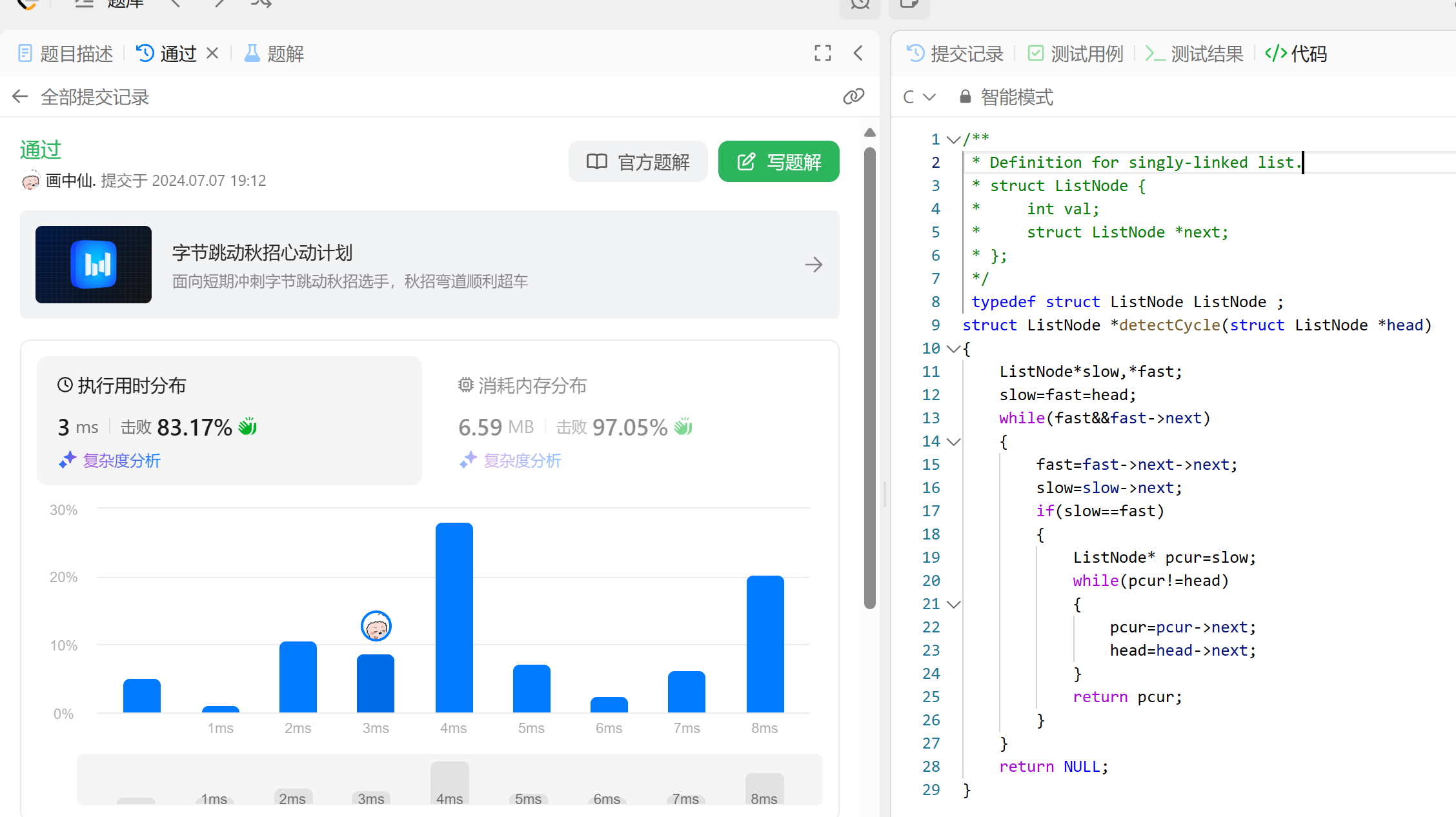
所以根据推导我们得出只要再相遇后,一个head指针从头节点出发,一个pcur节点从相遇点出发,等他们相遇时,相遇点就是入环点。

发表评论