目录
基本思想

简而言之就是,由已知的x(和y)训练得到模型f,再用模型f对训练集的x进行预测特征y。
基本方法
分类
利用已知标签的数据集进行模型训练,再利用模型对未分类的数据进行分类,预测标签。
回归
与分类相似,但分类输出是离散型变量,而回归输出是连续型变量。
聚类
聚类与前面两者都不一样,他不需要标签,是一种无监督学习,它是把相似的点聚集到同一类。
相关算法

线性回归
基本函数模型(y=b+wx)
y=b+wx式子中,y表示输出量,x表示输入特征量,b表示偏差,w表示权重。
一般步骤:
1.根据已知数据建立函数模型(函数集合)。
2.计算损失函数,利用损失函数对模型参数进行评估。
3.选出一组使平均损失最小的相关参数值。得到最优函数模型。
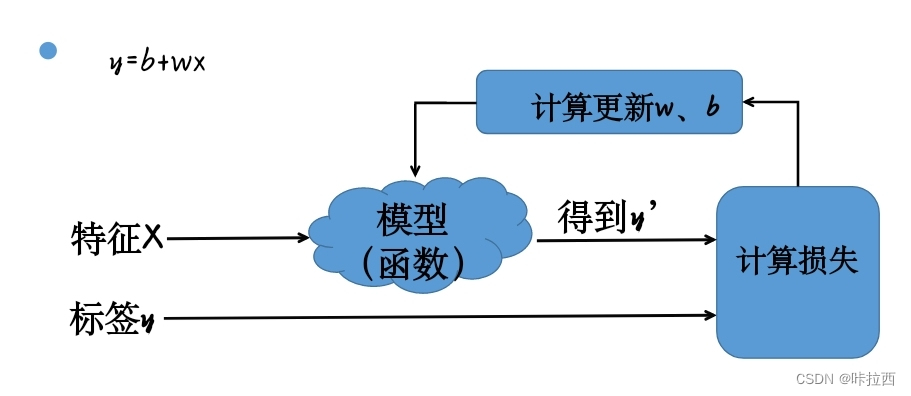
虽然我们得到了一般步骤,但是每一步具体应该怎么做呢?需要注意一些什么呢?那就接着往后看。
函数模型的建立
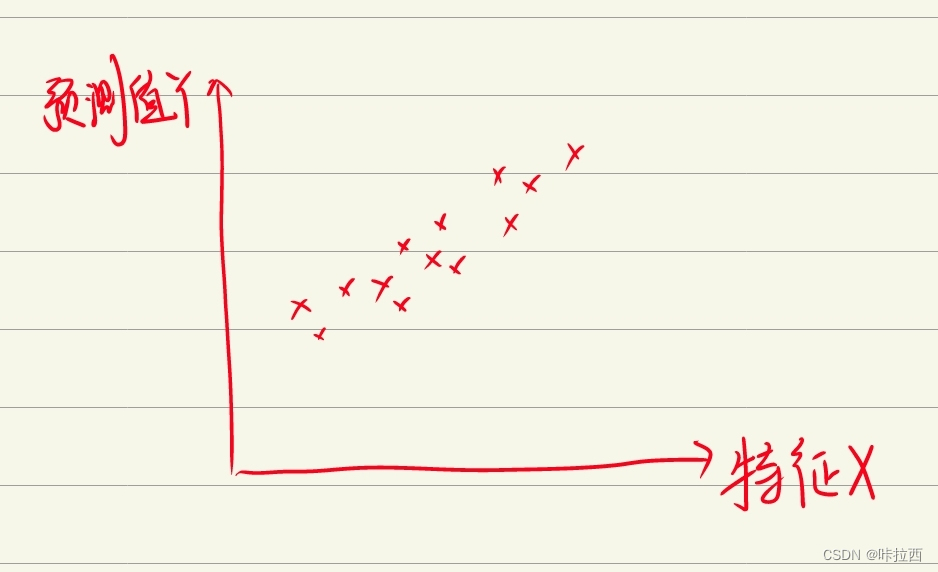
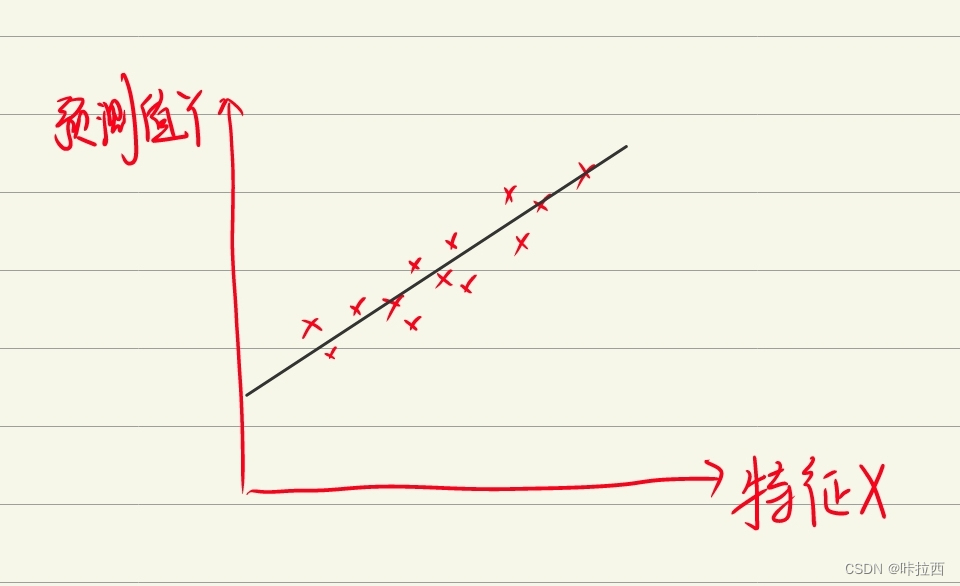
在这里,我就用简单的一元线性回归举例。由左图明显可以看出可以用一条直线进行拟合,而其这条直线不经过原点,当然,在这个例子中很明显不经过原点,在有的例子中不一定能看得出来但是我们依旧会加上一个截距,假如经过原点,训练得到得模型截距就为0,所以不影响我们对模型得训练。由于在这个例子中只有一个特征变量,我们只需要设置一个输入特征变量。综上所述,我们可以用y=b+wx来作为模型进行训练。
举一反三。假如离散得点用二次函数更加拟合,那边可以用y=b+wx^2;如果数据中有两个或者多个特征变量,那么函数模型也可以选择多元的函数,例如:y=b+w1*x1+w2*x2+……;同理更复杂的,其中x1,x2也可以加上平方,次方等幂。
损失函数
定义:
损失函数是指汇总各样本损失的数学函数,其损失函数有两种类型:
l1型(均绝对误差 mae):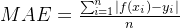
l2型(均方误差 mse):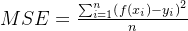
我们一般使用l2型损失函数。
由损失函数的定义,我们可以知道,当损失函数值最小时,函数模型的拟合效果最好。那么如何降低到最低点呢?
梯度下降法
假如我们把偏差b抹去,暂时不考虑。那么损失函数就是关于权重w的一个二元函数。
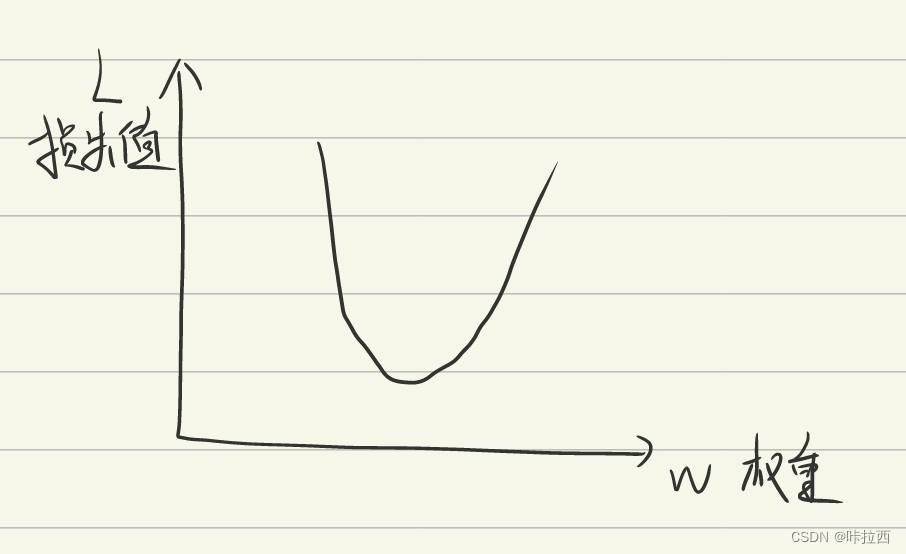
想要损失值取最小,那么就是要损失函数的斜率(即一阶导数)为0。同理,加上偏差后,损失函数就是关于偏差和权重的二元二次函数。这个时候,损失函数值就是关于b和w在空间中的像一个倒着的山丘。那么一样会出现一个最低点是损失值的最小值。知道了目标点了,但是那么我们要如何找到最低点呢?
不妨我们将偏导数命名为梯度,他是一个矢量,他的正负我们用来表示方向,而梯度的值是偏导数的绝对值。为了能尽快找到最低点,我把梯度值取当前点的绝对值最大的方向导数的绝对值。方向为导数的负方向,故更新数据应该用原来的数据减去梯度值。得:
梯度下降的算法: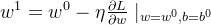
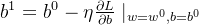
其中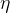 是学习率,他是控制梯度得大小。简单得可以认为是控制步幅。是人为控制的参数,也称为超参数。我在这里插入讲一下学习率对模型训练的影响
是学习率,他是控制梯度得大小。简单得可以认为是控制步幅。是人为控制的参数,也称为超参数。我在这里插入讲一下学习率对模型训练的影响
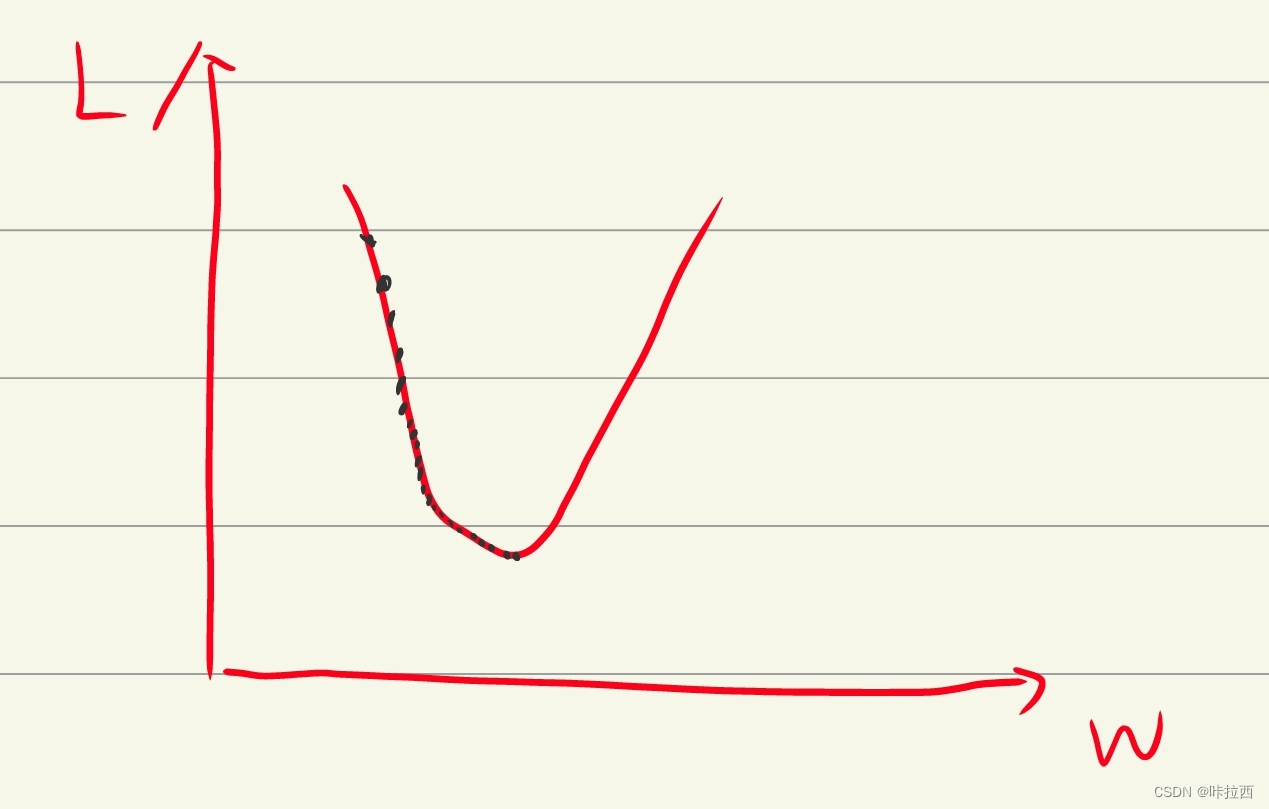
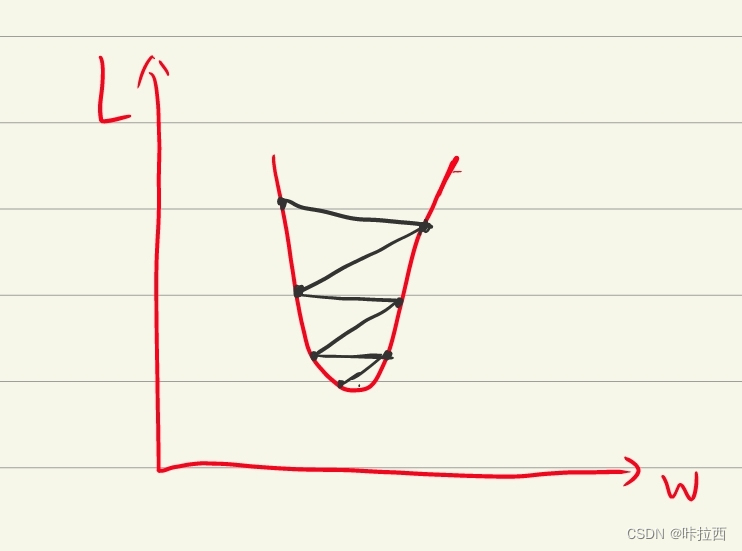
学习率过小,会导致步幅太小,收敛到最低点速度太慢,耗时较长。
学习率过大,会导致步幅过大,越过了最低点,难以收敛到最低点。
通过不断的迭代更新参数偏差b和权重w。最后直到损失值不再发生改变时,损失函数取得最小值,即得到最优拟合函数模型。
举个例子:
模型的选择:

定义损失函数

通过梯度下降迭代更新参数b和w,得到最优参数组合。便得到最优函数。



总结:
如何训练一个机器学习模型?
1.建立一个函数模型(y=b+wx)。
2.定义其函数的损失函数,用来评价函数模型的好坏,当损失函数值最小时,函数最优。
3.利用梯度下降找到最佳函数模型,也就是找到损失函数值最低的点。
制作不易,转载请告知博主,谢谢。希望能帮助到各位博主,欢迎大佬指错。

发表评论