从基础到高级应用解析Python中的序列类型_Python

引言：为什么序列如此重要？

在python编程世界中，序列（sequence） 是最基础、最常用的数据结构之一！无论是处理数据、构建算法，还是日常的脚本编写，序列都扮演着不可或缺的角色。想象一下，如果没有列表、元组、字符串这些序列类型，python编程将会变得多么困难！

今天，我将带你深入探索python序列的奥秘，从基础概念到高级应用，让你彻底掌握这一核心知识点！

1.python序列类型概述

1.1 什么是序列

序列是一个有序的元素集合**，每个元素都有其特定的位置（索引）。python中的序列具有以下共同特性：

有序性：元素按特定顺序排列
可索引：通过下标访问元素（从0开始）
可切片：可以获取子序列
可迭代：可以使用循环遍历
可计算长度：使用len()函数

1.2 主要序列类型对比

序列类型	可变性	是否有序	主要用途	示例
列表（list）	✅ 可变	✅ 有序	存储可变数据集合	[1, 2, 3]
元组（tuple）	❌ 不可变	✅ 有序	存储不可变数据	(1, 2, 3)
字符串（string）	❌ 不可变	✅ 有序	文本处理	"hello"
范围（range）	❌ 不可变	✅ 有序	生成数字序列	range(5)
字节数组（bytearray）	✅ 可变	✅ 有序	二进制数据处理	bytearray(b'abc')

2.序列类型详细分类

2.1 可变序列 vs 不可变序列

让我们通过一个流程图来理解序列的分类关系：

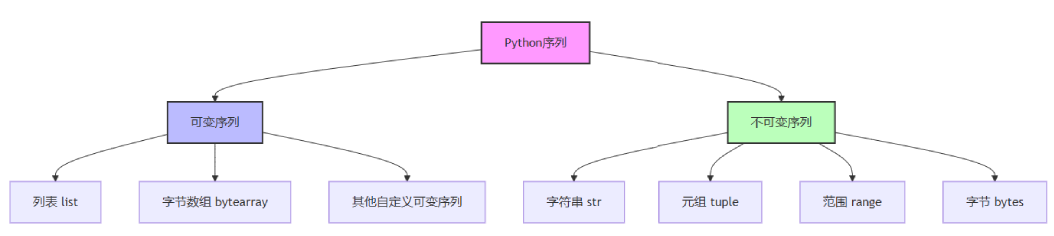
2.2 各种序列类型详解

列表（list） - 最灵活的序列

列表是python中最常用的可变序列，可以存储任意类型的元素：

# 创建列表的多种方式
fruits = ["apple", "banana", "cherry"]  # 直接创建
numbers = list(range(1, 6))            # 使用list()构造函数
mixed_list = [1, "hello", 3.14, true]  # 混合类型

# 列表操作示例
print(f"原始列表: {fruits}")
print(f"第一个水果: {fruits[0]}")        # 索引访问
print(f"最后两个水果: {fruits[-2:]}")    # 切片操作
print(f"列表长度: {len(fruits)}")        # 获取长度

# 修改列表
fruits.append("orange")                # 添加元素
fruits.insert(1, "blueberry")          # 插入元素
fruits[2] = "strawberry"               # 修改元素
print(f"修改后的列表: {fruits}")

元组（tuple） - 不可变的守护者

元组是不可变序列，常用于存储不应被修改的数据：

# 创建元组
coordinates = (10, 20)
colors = "red", "green", "blue"  # 括号可省略
single_tuple = (42,)             # 单元素元组必须有逗号

# 元组解包（超实用功能！）
x, y = coordinates
print(f"坐标: x={x}, y={y}")

# 元组作为函数返回值
def get_min_max(numbers):
    return min(numbers), max(numbers)

min_val, max_val = get_min_max([5, 2, 8, 1, 9])
print(f"最小值: {min_val}, 最大值: {max_val}")

字符串（string） - 文本处理专家

字符串是不可变字符序列，python提供了丰富的字符串操作方法：

text = "python序列编程指南"

# 字符串操作
print(f"字符串长度: {len(text)}")
print(f"前6个字符: {text[:6]}")
print(f"是否以'python'开头: {text.startswith('python')}")
print(f"查找'序列'的位置: {text.find('序列')}")

# 字符串方法链式调用
result = "  hello, world!  ".strip().upper().replace("world", "python")
print(f"处理后的字符串: {result}")

3.序列协议深入解析

3.1 什么是序列协议

序列协议是python中定义序列行为的约定。任何实现了特定方法的对象都可以被视为序列。这些方法包括：

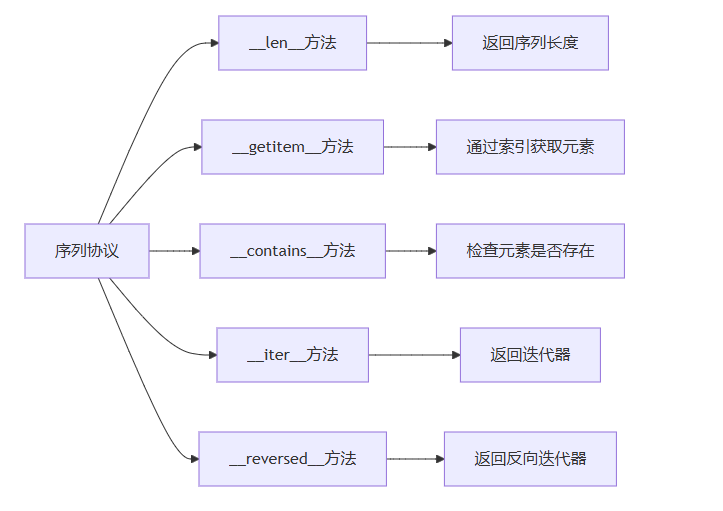
3.2 实现自定义序列类

让我们创建一个简单的自定义序列类来理解序列协议：

class fibonaccisequence:
    """自定义斐波那契数列序列"""
    
    def __init__(self, n):
        self.n = n
        self._sequence = self._generate_fibonacci()
    
    def _generate_fibonacci(self):
        """生成斐波那契数列"""
        if self.n <= 0:
            return []
        elif self.n == 1:
            return [0]
        
        fib = [0, 1]
        for i in range(2, self.n):
            fib.append(fib[-1] + fib[-2])
        return fib
    
    def __len__(self):
        """实现序列协议：返回长度"""
        return len(self._sequence)
    
    def __getitem__(self, index):
        """实现序列协议：索引访问"""
        if isinstance(index, slice):
            # 处理切片
            return self._sequence[index]
        elif 0 <= index < len(self._sequence):
            return self._sequence[index]
        elif -len(self._sequence) <= index < 0:
            return self._sequence[index]
        else:
            raise indexerror("索引超出范围")
    
    def __contains__(self, item):
        """实现序列协议：检查元素是否存在"""
        return item in self._sequence
    
    def __iter__(self):
        """实现序列协议：返回迭代器"""
        return iter(self._sequence)
    
    def __reversed__(self):
        """实现序列协议：返回反向序列"""
        return reversed(self._sequence)
    
    def __str__(self):
        return f"fibonaccisequence(前{self.n}项): {self._sequence}"

# 使用自定义序列
fib_seq = fibonaccisequence(10)
print(fib_seq)
print(f"长度: {len(fib_seq)}")
print(f"第5个元素: {fib_seq[4]}")
print(f"前5个元素: {fib_seq[:5]}")
print(f"是否包含13: {13 in fib_seq}")
print(f"反向遍历: {list(reversed(fib_seq))}")

3.3 序列操作性能分析

了解不同序列操作的性能对于编写高效代码至关重要：

操作	列表	元组	字符串	时间复杂度
索引访问	o(1)	o(1)	o(1)	常数时间
尾部追加	o(1)*	n/a	n/a	平均常数时间
头部插入	o(n)	n/a	n/a	线性时间
切片	o(k)	o(k)	o(k)	与切片大小相关
成员检查	o(n)	o(n)	o(n)	线性时间
连接	o(n+m)	o(n+m)	o(n+m)	与总长度相关

注：列表的append()操作平均为o(1)，但在需要扩容时为o(n)

4.实战应用案例

4.1 案例一：数据分析中的序列应用

# 模拟销售数据分析
def analyze_sales_data():
    # 使用列表存储每日销售额
    daily_sales = [1200, 1500, 1800, 900, 2100, 1700, 1900]
    
    # 使用元组存储日期
    days = ("周一", "周二", "周三", "周四", "周五", "周六", "周日")
    
    # 计算统计信息
    total_sales = sum(daily_sales)
    avg_sales = total_sales / len(daily_sales)
    max_sales = max(daily_sales)
    max_day = days[daily_sales.index(max_sales)]
    
    # 使用字符串格式化输出
    report = f"""
    📊 销售数据分析报告
    ====================
    总销售额: ¥{total_sales:,.2f}
    平均日销售额: ¥{avg_sales:,.2f}
    最高销售额: ¥{max_sales:,.2f} ({max_day})
    
    每日销售详情:
    """
    
    # 使用zip组合两个序列
    for day, sales in zip(days, daily_sales):
        report += f"    {day}: ¥{sales:,.2f}\n"
    
    return report

print(analyze_sales_data())

4.2 案例二：序列在算法中的应用

# 使用序列实现简单的lru缓存
class lrucache:
    """最近最少使用缓存"""
    
    def __init__(self, capacity):
        self.capacity = capacity
        self.cache = {}  # 存储键值对
        self.order = []  # 使用列表维护访问顺序
    
    def get(self, key):
        """获取缓存值"""
        if key in self.cache:
            # 更新访问顺序：移动到列表末尾
            self.order.remove(key)
            self.order.append(key)
            return self.cache[key]
        return -1
    
    def put(self, key, value):
        """添加缓存项"""
        if key in self.cache:
            # 更新现有键
            self.cache[key] = value
            self.order.remove(key)
            self.order.append(key)
        else:
            # 添加新键
            if len(self.cache) >= self.capacity:
                # 移除最久未使用的键
                lru_key = self.order.pop(0)
                del self.cache[lru_key]
            
            self.cache[key] = value
            self.order.append(key)
    
    def __str__(self):
        return f"lrucache(容量={self.capacity}, 内容={self.cache}, 顺序={self.order})"

# 测试lru缓存
cache = lrucache(3)
cache.put("a", 1)
cache.put("b", 2)
cache.put("c", 3)
print(f"初始状态: {cache}")

cache.get("a")  # 访问a，使其成为最近使用的
cache.put("d", 4)  # 添加d，应该移除b（最久未使用）
print(f"添加d后: {cache}")

5.高级技巧与最佳实践

5.1 序列推导式（comprehensions）

python提供了简洁的语法来创建序列：

# 列表推导式
squares = [x**2 for x in range(10)]
even_squares = [x**2 for x in range(10) if x % 2 == 0]

# 生成器表达式（内存效率更高）
large_squares = (x**2 for x in range(1000000))

# 字典推导式
square_dict = {x: x**2 for x in range(5)}

print(f"平方列表: {squares[:5]}...")
print(f"偶数平方: {even_squares}")
print(f"平方字典: {square_dict}")

5.2 序列解包的高级用法

# 扩展解包
first, *middle, last = [1, 2, 3, 4, 5]
print(f"第一个: {first}, 中间: {middle}, 最后一个: {last}")

# 嵌套解包
points = [(1, 2), (3, 4), (5, 6)]
for x, y in points:
    print(f"点坐标: ({x}, {y})")

# 交换变量（pythonic方式！）
a, b = 10, 20
a, b = b, a  # 不需要临时变量！
print(f"交换后: a={a}, b={b}")

5.3 性能优化建议

1.选择合适的序列类型：

需要修改数据？使用列表
数据不变？使用元组
处理文本？使用字符串

2.避免不必要的复制：

# 不好：创建完整副本
new_list = old_list[:]

# 更好：使用切片或list()构造函数
new_list = list(old_list)

3.使用生成器处理大数据：

# 处理大文件时使用生成器
def read_large_file(file_path):
    with open(file_path, 'r') as file:
        for line in file:
            yield line.strip()

总结与展望

通过本文的深入探讨，我们全面了解了python序列类型的世界：

掌握了序列的基本概念和分类
深入理解了序列协议的工作原理
学会了如何实现自定义序列
了解了各种序列操作的性能特征
掌握了序列在实际项目中的应用技巧

序列是python编程的基石，熟练掌握序列操作将极大提升你的编程效率和代码质量。随着python版本的更新，序列功能也在不断增强（如python 3.8+的海象运算符、3.10的模式匹配等），持续学习是保持竞争力的关键！

记住：优秀的python程序员不仅是序列的使用者，更是序列的大师！

到此这篇关于从基础到高级应用解析python中的序列类型的文章就介绍到这了,更多相关python序列类型内容请搜索代码网以前的文章或继续浏览下面的相关文章希望大家以后多多支持代码网！

从基础到高级应用解析Python中的序列类型

2026年01月27日 • Python •我要评论